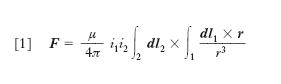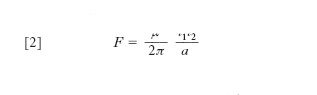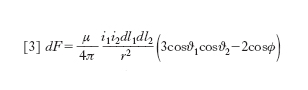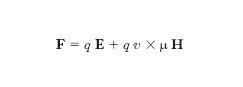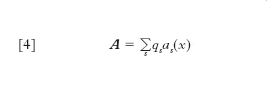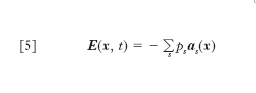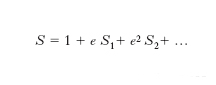elettrodinamica

Parte della elettrologia che ha per oggetto lo studio delle mutue azioni fra circuiti percorsi da corrente ( azioni elettrodinamiche) e, più in generale, delle interazioni fra cariche in moto e campi elettromagnetici. Se la trattazione viene fatta senza ricorrere ai principi e ai risultati della meccanica quantistica, cioè nei termini della sistemazione maxwelliana dell’elettromagnetismo, si parla di e. classica; altrimenti, si parla di e. quantistica. Si parla poi di e. relativistica quando le velocità in gioco sono così grandi da rendere necessaria la trattazione nei termini della teoria della relatività.

E. classica

Ci si limita qui alla trattazione delle azioni meccaniche fra circuiti elettrici (per gli aspetti più generali, e in particolare per l’interazione fra campi e correnti ➔ elettromagnetismo). La forza che un circuito 1, di forma qualunque, percorso da una corrente di intensità i₁ esercita su un circuito 2 percorso da una corrente di intensità i₂ si può calcolare (in unità del sistema internazionale) con la formula:

[1] formula,

in cui μ è la permeabilità magnetica assoluta del mezzo dove i due circuiti si trovano, dl₁, dl₂ sono due elementi rispettivamente del circuito 1 e del circuito 2, uscenti il primo da un punto A₁ e il secondo da un punto A₂, orientati nel verso della corrente, r è il vettore A₁ A₂ (avente origine nel punto A₁ ed estremo nel punto A₂). La [1], nota anche come legge di Ampère, proviene da una opportuna successiva applicazione delle due leggi di Laplace dell’elettromagnetismo; ha grande importanza pratica, anche se la sua applicazione può offrire difficoltà analitiche derivanti dal calcolo dei due integrali curvilinei. Nel caso particolare di due fili rettilinei, paralleli, di dimensioni trasversali molto piccole rispetto alla distanza a tra i fili, la [1] dà per la forza F per unità di lunghezza l’espressione:

[2] formula;

la forza è attrattiva se le due intensità di corrente i₁e i₂ sono equiverse, repulsiva nel caso contrario. Se il mezzo è il vuoto (μ=4π 10^–7 H/m), a=1 m e i₁= i₂= 1 A, risulta F=2‧10⁻⁷ N/m (➔ Ampère). Si noti che non avrebbe alcun senso fisico il voler ricavare con lo stesso criterio (cioè con una successiva applicazione delle due leggi di Laplace) una legge elettrodinamica elementare, cioè una espressione per l’azione elettrodinamica esercitantesi fra un elemento del primo circuito e un elemento del secondo. Infatti la 1^a legge elementare di Laplace non ha un contenuto reale, non essendo possibile attribuire un significato fisico a un elemento di corrente isolato dal resto del circuito. La legge è accettabile in quanto, applicata a circuiti chiusi, dà risultati in accordo con l’esperienza. Per questa ragione, volendo esprimere la forza dF che si esercita fra due elementi si deve piuttosto ricorrere a una legge elementare postulata indipendentemente dalle leggi di Laplace. Fra le varie leggi proposte merita d’esser ricordata la legge elementare elettrodinamica di Ampère: l’azione che l’elemento dl₁ del primo circuito esercita sull’elemento dl₂ del secondo circuito, misurata secondo la retta orientata A₁A₂, è data in valore e segno da

[3] formula,

fig. 1

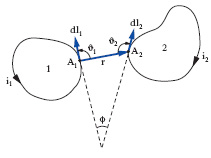
dove i simboli già usati nella [1] hanno lo stesso significato, ϑ₁ è l’angolo che A₁A₂ forma con dl₁, ϑ₂ l’angolo che A₂A₁ forma con dl₂, ϕ l’angolo tra dl₁ e dl₂ (fig. 1). La forza che dl₂esercita su dl₁ è uguale e contraria a quella che dl₁ esercita su dl₂, avendo entrambe la retta d’azione A₁A₂ (in modo da soddisfare il principio di azione e reazione); a seconda che dF>0 oppure dF〈0, le azioni sono repulsive o attrattive.

E. quantistica
Definizione

- È la teoria quantistica relativistica delle interazioni del campo elettromagnetico con la materia, e in particolare con particelle elementari di spin 1/2 (tipicamente l’elettrone). Il suo sviluppo si è reso necessario per poter formulare in termini corpuscolari (e compatibili con la teoria della relatività) la descrizione ondulatoria classica del campo elettromagnetico. Nei termini di quest’ultima (➔ elettromagnetismo) il campo stesso è rappresentato da due vettori, il campo elettrico E e il campo magnetico H, le cui proprietà nello spazio e nel tempo sono descritte dalle equazioni di Maxwell. L’azione F del campo su una particella di massa m, carica q e velocità v è:

,

dove μ è la permeabilità magnetica assoluta del mezzo in cui avviene l’interazione; alla particella in questione viene impressa l’accelerazione a=F/m: la velocità, e con essa la quantità di moto e l’energia della particella variano quindi da istante a istante e da punto a punto del campo. In base al teorema della conservazione dell’energia e della quantità di moto applicato al sistema isolato particella-campo l’energia e la quantità di moto acquistate o perdute dalla particella debbono essere cedute o assorbite dal campo: ciò è sempre possibile nella e. classica, ove energia e quantità di moto del campo elettromagnetico sono grandezze continue, che possono quindi variare anche per quantità piccole a piacere. In realtà, come clamorosamente venne in luce con la scoperta e l’interpretazione dell’effetto fotoelettrico (➔ fotoelettrone), tale modo di vedere le cose è inaccettabile: l’energia delle onde elettromagnetiche si trasferisce per quanti (fotoni), di massa nulla, energia hν e quantità di moto hν/c, essendo h la costante di Planck, c la velocità delle onde nel vuoto, ν la loro frequenza.

Cenni storici

- I fondamenti dell’e. quantistica furono stabiliti principalmente a opera di P.A.M. Dirac, W.K. Heisenberg, W. Pauli ed E. Fermi tra il 1928 e il 1930, quando già aveva ricevuto il suo assetto definitivo la meccanica quantistica (➔ meccanica), con la quale l’e. quantistica costituisce la cosiddetta teoria dei quanti. L’interazione del campo elettromagnetico con la materia viene studiata considerando come un unico sistema campo e particelle materiali, e assegnando a tale sistema un’ hamiltoniana (➔ Hamilton, sir Willian Rowan) pari alla somma dell’hamiltoniana del campo e delle hamiltoniane delle particelle più un opportuno ‘termine di interazione’, in modo da ottenere una descrizione in termini relativisticamente invarianti. La prima formulazione di tale genere fu la cosiddetta teoria della radiazione di Dirac (1927), che dette una spiegazione del tutto soddisfacente dei fenomeni di assorbimento, emissione e diffusione della luce da parte di sistemi atomici.

La successiva formulazione, oltre a contenere tutti i risultati della teoria della radiazione di Dirac, fornì una buona descrizione di un gran numero di fatti sperimentali, riguardanti l’interazione delle particelle cariche con il campo elettromagnetico. I fenomeni più importanti sono i seguenti: effetto Compton (O. Klein e H. Nishina, 1929; ➔ Compton, Arthur Holly), annichilazione di coppie elettrone-positrone con emissione di fotoni (Dirac, 1930, H.A. Bethe, 1935), creazione di coppie (Bethe e W. Heitler, 1934), Bremsstrahlung, cioè irraggiamento di fotoni da parte di una particella carica frenata (radiazione di frenamento, Bethe e Heitler, 1934). Negli anni 1949-50 si verificò un nuovo sostanziale progresso, dovuto principalmente a S. Tomonaga e collaboratori, a R.P. Feynman, a J. Schwinger e a F.J. Dyson, progresso che ha condotto in sostanza all’e. quantistica nella forma attuale.

Gli sviluppi teorici successivi sono di minor rilievo, consistendo piuttosto in raffinamenti formali che in progressi sostanziali. Degne comunque di nota sono le riformulazioni dell’e. quantistica e, più in generale, della teoria quantistica del campo, dovute a H. Lehmann, K. Simanzik e N. Zimmermann, e ad A.S. Wightman; quest’ultima formulazione ha costituito il punto di partenza del cosiddetto approccio assiomatico, che ha poi preso diverse forme, tutte miranti a porre la teoria su basi estremamente rigorose dal punto di vista formale.

Aspetti teorici

- Poiché l’e. quantistica è la teoria quantistica relativistica di un campo spinoriale, descrivente una particella elementare carica di spin 1/2 (tipicamente l’elettrone) in interazione con il campo elettromagnetico (cui corrisponde, nella teoria quantistica, una particella di spin 1 e massa nulla, il fotone), l’esistenza di particelle elementari di spin 0, 1, 3/2 ecc., dotate di carica elettrica, e pertanto anch’esse interagenti col campo elettromagnetico, richiede che la teoria venga estesa anche al caso di campi scalari (cui corrispondono particelle di spin 0), vettoriali (cui corrispondono particelle di spin 1) ecc., in interazione con il campo elettromagnetico. Tutti questi casi rientrano nel più generale ambito della teoria quantistica relativistica dei campi, che costituisce la base della moderna teoria delle particelle elementari (➔).

L’idea fondamentale dell’e. quantistica (e, più in generale, della teoria quantistica dei campi) è quella di considerare un campo classico come un sistema dinamico con un numero infinito di gradi di libertà e d’imporre condizioni di quantizzazione suggerite dall’analogia con il caso dei sistemi a un numero finito di gradi di libertà; essa è però anche quella di formulare direttamente, in forma assiomatica, una teoria quantistica generale, senza alcun riferimento a una preesistente teoria classica da quantizzare. La possibilità di operare diverse scelte delle variabili dinamiche descriventi il sistema permette di trattare nell’ambito di una stessa teoria unitaria gli aspetti corpuscolari (le particelle, per es., i fotoni e gli elettroni, sono i quanti dei rispettivi campi, elettromagnetico e spinoriale) e ondulatori (diffrazione, interferenza ecc.). Tali diversi aspetti si manifestano in diverse situazioni sperimentali, in modo complementare (nel senso del principio di complementarità; ➔ Bohr, Niels Henrik David). Le diverse versioni dell’e. quantistica si distinguono per il punto di vista e per il grado di rigore matematico; in ogni caso la condizione d’invarianza relativistica gioca un ruolo essenziale. Dal punto di vista formale la teoria, quale che sia la sua formulazione, è notevolmente complessa; non si presta a un’esposizione semplice, richiedendo l’uso di formalismi matematici non elementari.

Dal punto di vista pratico, le principali formulazioni sono completamente equivalenti e conducono generalmente a una prescrizione per il calcolo delle grandezze fisiche nella forma di uno sviluppo perturbativo, cioè una serie i cui successivi termini sono proporzionali a potenze intere crescenti di un parametro adimensionale, la cosiddetta costante di struttura fina, α=e²/ħc, dove ħ è la costante di Planck divisa per 2π, c è la velocità della luce nel vuoto ed e è la carica elettrica elementare. Il piccolo valore numerico della costante di struttura fina, pari circa a 1/137, implica che i successivi termini di tale sviluppo sono generalmente di grandezza nettamente decrescente; ciò costituisce la giustificazione di calcoli che si limitino ai soli primi termini, cosa inevitabile per il rapido aumento delle difficoltà di calcolo con l’ordine. Il punto di vista perturbativo ha anche il pregio di analizzare i fenomeni fisici in termini di processi elementari, consistenti nell’emissione di fotoni da parte di elettroni o positroni e nella trasmutazione di un fotone in una coppia elettrone-positrone, nonché nei processi inversi (assorbimento di un fotone, annichilazione di una coppia elettrone-positrone in un fotone). Le particelle coinvolte in questi processi possono risultare effettivamente presenti nel fenomeno fisico (particelle reali), ovvero possono manifestarsi solo tramite la loro influenza sul comportamento delle particelle reali (particelle virtuali): per es., in un esperimento di diffusione elastica di due particelle cariche (due elettroni, o un elettrone e un positrone) solo due particelle sono realmente presenti, ma l’interazione elettromagnetica fra di loro, che condiziona il loro comportamento (per es., determina la probabilità che le loro traiettorie risultino deflesse di un certo angolo) può essere associata allo scambio di fotoni virtuali emessi e assorbiti dalle due particelle. Questo tipo di descrizione acquista un preciso significato con l’uso dei diagrammi di Feynman, che costituiscono un utile strumento interpretativo dei fenomeni fisici e forniscono la più conveniente tecnica di calcolo nell’ambito del procedimento perturbativo.

Divergenze e rinormalizzazione

- Una caratteristica dell’e. quantistica (e, più in generale, delle teorie quantistiche relativistiche) è quella di dar luogo a divergenze; s’incontrano cioè nel corso dei calcoli di tipo perturbativo di cui si è detto più sopra (e che sono peraltro gli unici che conducano a risultati effettivamente confrontabili con i dati sperimentali) degli integrali che risultano divergenti. Evidentemente la teoria è utilizzabile solo se è possibile dare prescrizioni univoche per eliminare tali divergenze. Ciò è fatto usando una tecnica proposta e discussa da H. Bethe e altri nel 1947 e successivamente perfezionata. Fu allora osservato che i contributi divergenti si limitano a modificare i valori della carica elettrica delle particelle interagenti col campo elettromagnetico, nonché i valori delle loro masse (aggiungendo alla massa ‘nuda’ una massa ‘elettromagnetica’). Sicché, se i risultati finali vengono espressi in funzione della massa e della carica così corrette (che coincidono del resto, nell’ambito stesso della teoria, con la massa e carica sperimentalmente osservabili), la teoria risulta depurata di ogni divergenza. Il processo ora descritto prende il nome di rinormalizzazione (di massa e di carica), e permette di predire qualunque processo fisico in modo non ambiguo e con arbitraria precisione (salvo le difficoltà di calcolo, che peraltro possono ora essere parzialmente superate usando calcolatori elettronici per effettuare anche parte degli sviluppi analitici, facendo uso di appositi algoritmi).

Problemi aperti

- L’e. quantistica è, come si è detto, in grado di formulare predizioni quantitative, che risultano verificate con una precisione estrema. In questo senso si può affermare che essa costituisce la più fondamentale e accurata teoria fisica oggi esistente. Essa ha inoltre coronato il profondo processo di rinnovamento della fisica, determinato nella prima metà del 20° sec. dall’avvento della teoria della relatività ristretta e della meccanica quantistica, rappresentando la fusione coerente di tali innovazioni, e fornendo la più esauriente spiegazione del dualismo onda-corpuscolo. Essa fornisce infine il modello di base della teoria quantistica dei campi, che costituisce una soddisfacente, anche se tuttora incompleta, spiegazione delle proprietà fondamentali della natura, al più elementare livello microscopico attingibile con le moderne tecniche sperimentali. Tuttavia la necessità di ricorrere, per ogni calcolo, a tecniche di tipo perturbativo è una limitazione grave, tanto più in quanto la comparsa di divergenze in tali calcoli suggerisce che la serie perturbativa non converge. La tecnica della rinormalizzazione, pur permettendo di eliminare le divergenze e di ottenere risultati confrontabili con i dati sperimentali, non può essere considerata una soluzione soddisfacente, se non altro perché non permette di calcolare alcune grandezze, quali le differenze di massa di origine elettromagnetica, che è difficile credere non abbiano senso fisico (si pensi al caso dei pioni o dei nucleoni, con differenza di massa finita fra particelle neutre e cariche). L’e. quantistica è caratterizzata inoltre dal parametro adimensionale α, legato al valore della carica elettrica, ma né il valore numerico di tale costante né il fatto che la carica elettrica di tutte le particelle elementari è un piccolo multiplo intero della stessa carica elettrica elementare sono spiegati dalla teoria.

Sviluppi formali

- L’e. quantistica può essere sviluppata assumendo come concetto base il fotone o, in alternativa, l’idea di campo elettromagnetico, come sistema a infiniti gradi di libertà accoppiato agli elettroni. Seguendo questa seconda via, il campo elettromagnetico può essere quantizzato con il metodo utilizzato da Fermi, basato sull’osservazione che il campo elettromagnetico racchiuso entro una cavità vuota a pareti riflettenti si può considerare come una sovrapposizione di infiniti campi parziali, distinti da un indice s=1, 2, ..., ognuno dei quali compie oscillazioni sinusoidali con una sua frequenza caratteristica ν_s. Questo comportamento è del tutto simile a quello di un sistema dinamico che compie piccole oscillazioni intorno a una posizione di equilibrio. Ognuno dei campi parziali, considerato da solo, corrisponde a un’onda elettromagnetica stazionaria, che ha una sua caratteristica distribuzione nello spazio. Così, per esempio, il potenziale vettore A(x, t), da cui si deduce di solito il campo magnetico H=rot A, si può esprimere a un dato istante mediante una serie in cui, nel caso generale, vanno incluse sia onde trasversali (div α=0) sia onde longitudinali (rot α=0):

[4] formula;

in questa serie i termini corrispondenti a s=1, 2, ... sono appunto i campi parziali; le funzioni caratteristiche a_s si ottengono risolvendo un problema di autovalori legato alla forma e alle dimensioni della cavità. I coefficienti q₁, q₂, q_s, ... dello sviluppo si possono considerare come coordinate lagrangiane generali del sistema o, se si vuole, come le coordinate di altrettanti oscillatori, che nel loro insieme costituiscono il campo elettromagnetico. Le equazioni del moto di questi oscillatori altro non sono che le equazioni di Maxwell in veste diversa. Le oscillazioni dei campi parziali non saranno più indipendenti le une dalle altre, né strettamente sinusoidali, se entro la cavità vi sono particelle cariche, le quali generano le densità di carica e di corrente che compaiono come termini non omogenei a secondo membro delle equazioni di Maxwell. In questa situazione la presenza delle cariche e i loro movimenti modificano il campo, mentre questo a sua volta agisce sul moto delle cariche; indirettamente, ne risulta un accoppiamento tra i vari oscillatori del campo. Nella forma hamiltoniana delle equazioni del moto compaiono, accanto alle q₁, q₂, ..., le variabili coniugate p₁, p₂, ..., le quali sono del resto uguali, a parte il segno, ai coefficienti dello sviluppo, analogo alla [4], del campo elettrico E a un dato istante:

[5] formula.

La quantizzazione di questo schema ha luogo estendendo alle variabili q_s, p_s (s=1, 2, ...) le regole di commutazione già ammesse per gli ordinari sistemi dinamici a n gradi di libertà; in particolare, per una q_s e il corrispondente momento p_s, la regola:

[5] [q_s, p_s] ≡ q_sp_s − p_sq_s = i ℏ,

mentre, invece, q_s e p_r (con s ≠r), due diverse q o due diverse p commutano una con l’altra. Ciò implica che i valori delle q e delle p a un dato istante non sono ordinari numeri reali ma elementi di un’algebra non commutativa, più precisamente matrici o anche operatori lineari in uno spazio hilbertiano. Conclusioni analoghe a quelle illustrate valgono anche, grazie alle relazioni [4] e [5], per le componenti E_i (x) e H_k (x¹) (i, k = 1, 2, 3) del campo elettrico e magnetico in due qualsiasi punti dello spazio.

Lo scopo dell’e. quantistica è quello di calcolare la probabilità che una data configurazione fisica iniziale evolva in una certa configurazione finale. L’e. quantistica con i metodi perturbativi, consente di studiare, calcolandone la rispettiva ampiezza di transizione (cioè la probabilità), l’evoluzione di una data configurazione fisica iniziale in una finale che può in generale contenere particelle diverse da quelle iniziali. L’ampiezza di transizione per un intervallo di tempo finito viene chiamata funzione di Green per il processo considerato; nel limite di tempo infinito le ampiezze di probabilità (dette anche ampiezze di diffusione) sono date dagli elementi della cosiddetta matrice S (dall’iniziale dell’inglese scattering e del tedesco Streuung, «diffusione»).

La matrice S, o matrice d’urto, riunisce in un solo schema le ampiezze di probabilità di tutti i possibili fenomeni d’urto in cui intervengono come particelle incidenti (stato iniziale) o uscenti (stato finale) fotoni, elettroni e positroni. Possiamo pensare che lo stato iniziale sia specificato assegnando la quantità di moto e lo stato di polarizzazione (ossia una componente dello spin) di ogni particella, e lo stato finale in modo analogo. L’insieme dei dati che caratterizzano uno stato si può indicare con una sola lettera, come a, b ecc., si può allora designare con il simbolo S_ab l’ampiezza di probabilità per la transizione dallo stato iniziale b allo stato finale a. La matrice S non è altro che l’insieme di questi simboli disposti come gli elementi di una matrice (S_ab). Si dimostra che l’operatore rappresentato da questa matrice è unitario e relativisticamente invariante. La prima di queste proprietà corrisponde alla proposizione che la somma delle probabilità di tutti i possibili stati finali deve essere uguale a uno; la seconda corrisponde al fatto che la relazione tra stato finale e stato iniziale è indipendente dal sistema di riferimento. Una delle forme invarianti della teoria delle perturbazioni consiste nello sviluppare in serie di potenze di e l’operatore S; il termine d’ordine zero è l’unità (il che significa che senza interazione non vi sono urti: lo stato iniziale è uguale a quello finale). Si ha cioè:

Si dimostra che, in assenza di un campo esterno, è S₁=0, cioè tutti i processi cominciano almeno al secondo ordine.

fig. 2

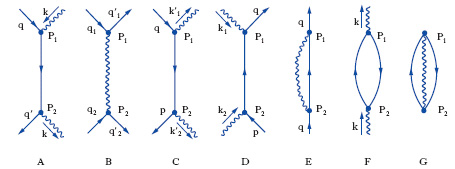
I vari termini della serie perturbativa possono essere rappresentati graficamente in modo molto suggestivo, secondo uno schema dovuto a R.P. Feynman ( diagrammi di Feynman). A ogni diagramma ed elemento di esso corrispondono precise regole per il calcolo dei contributi alla matrice S. L’n-esimo termine della serie perturbativa rappresenta n interazioni successive fra il campo elettromagnetico, che soddisfa le equazioni di Maxwell, e quello dell’elettrone, che soddisfa l’equazione di Dirac. Il diagramma contiene n vertici, in ognuno dei quali ha luogo l’interazione fra elettroni, fotoni e positroni. A ciascun vertice si possono applicare, per es., le seguenti operazioni: creazione o distruzione di un fotone; creazione di un elettrone o annichilazione di un positrone; annichilazione di un elettrone o creazione di un positrone. La fig. 2 rappresenta i termini del secondo ordine (n=2) della serie perturbativa della matrice S. Il primo diagramma (A) rappresenta l’interazione fra un elettrone e un fotone, cioè l’effetto Compton. Le linee ondulate rappresentano i fotoni, le linee continue gli elettroni e i positroni. Il simbolo k rappresenta il tetravettore energia-quantità di moto del fotone, mentre p e q rappresentano i tetravettori energia-quantità di moto rispettivamente dell’elettrone e del positrone. Le frecce entranti nel vertice indicano annichilazione, quelle uscenti creazione. I successivi diagrammi rappresentano, rispettivamente, i seguenti processi: B) l’interazione elettrone-elettrone; C) la produzione di coppie di fotoni a seguito dell’annichilazione di una coppia elettrone-positrone; D) la produzione di una coppia elettrone-positrone a causa dell’interazione fotone-fotone; E) l’interazione di un elettrone o di un positrone con il campo di radiazione originato dalla carica stessa; F) la creazione e la successiva distruzione di una coppia virtuale elettrone-positrone da parte di un fotone; G) la creazione e la successiva distruzione di una coppia elettrone-positrone da parte di un fotone anch’esso in uno stato virtuale, cioè in uno stato in cui la quantità di moto, la massa e l’energia di elettrone e fotone non soddisfano le relazioni della meccanica relativistica. I diagrammi E, F e G sono responsabili delle già citate divergenze in e. quantistica. La nube di fotoni virtuali (diagramma E) che accompagna un elettrone aumenta l’energia dell’elettrone; questo incremento può essere interpretato come un incremento di massa. La massa m dell’elettrone libero, non sottoposto ad alcuna interazione, non coincide quindi con la massa sperimentale m_sp dell’elettrone: essa è la somma della massa m e della massa m_em della nube dei fotoni che rappresentano l’azione del campo elettromagnetico. Questi ultimi fotoni, come si può vedere dal diagramma E stesso, vengono emessi e riassorbiti dall’elettrone nel processo d’interazione. La procedura di rinormalizzazione (della massa), che permette di regolarizzare le divergenze provenienti dal termine m_em, consiste nell’attribuire il valore −∞ a m e nell’imporre che m_sp sia uguale al valore della massa sperimentale dell’elettrone. Una procedura simile (in questo caso, di rinormalizzazione di carica) si applica ai diagrammi F e G che danno luogo a divergenze della carica elettrica.

Il confronto con i dati sperimentali

- È da osservare che una conseguenza importante dell’e. quantistica è che una particella carica può emettere e assorbire fotoni anche in assenza di un campo elettromagnetico esterno: si hanno cioè ‘fluttuazioni’ del vuoto. Esse hanno importanti conseguenze sperimentali, quali l’emissione spontanea di radiazione da parte di un atomo eccitato, lo spostamento dei livelli energetici dell’atomo di idrogeno (Lamb shift; ➔ Lamb, W.E.) e l’esistenza di una correzione radiativa del momento magnetico dell’elettrone e del muone. Affinché i risultati sperimentali possano mettere alla prova le previsioni dell’e. quantistica, è necessario che si riferiscano a processi che coinvolgono particelle che interagiscono con il campo elettromagnetico (e, naturalmente, fra loro, per il tramite del campo elettromagnetico), ma non risentono delle interazioni forti, che maschererebbero gli effetti elettrodinamici. La presenza di interazioni deboli non disturba, perché esse sono trascurabili (o appena al limite della confrontabilità) rispetto alle più fini correzioni di tipo elettromagnetico finora considerate, almeno a energie non molto elevate (≲ 10 GeV; il peso relativo delle interazioni elettromagnetiche e deboli si sposta a favore di queste ultime al crescere dell’energia), e a maggior ragione è trascurabile l’interazione gravitazionale. Tipici fenomeni elettrodinamici sono dunque: il momento magnetico di particelle cariche non soggette a interazioni forti (elettroni e muoni), gli stati legati del sistema costituito da un protone e un elettrone (atomo d’idrogeno) o da un elettrone e un positrone (positronio; questo sistema è però instabile, per la possibilità della coppia elettrone-positrone di annichilarsi, dando luogo a 2 o 3 fotoni), gli urti di un fotone su un elettrone (effetto Compton), di due elettroni fra loro o di un elettrone con un positrone, processo quest’ultimo particolarmente interessante perché può dar luogo a diffusione elastica, o all’annichilazione della coppia elettrone-positrone con creazione di due o più fotoni, o, se l’energia è sufficiente, di nuove particelle. Quest’ultimo processo è stato particolarmente studiato negli ultimi decenni, grazie alla realizzazione degli anelli di accumulazione.

L’e. quantistica è stata sottoposta a verifiche sperimentali estremamente accurate. Gli esperimenti, condotti da bassissime energie (meV) a energie superiori ai 10 GeV indicano che essa descrive correttamente tutti i fenomeni elettromagnetici macroscopici e quelli microscopici fino a distanze di circa 10⁻¹⁸ m (un millesimo della dimensione dei nuclei), al di sotto delle quali di cominciano a manifestare gli effetti delle interazioni deboli. Fra le verifiche a basse energia si possono citare quelle relative alle seguenti grandezze: a) il Lamb shift dell’atomo di idrogeno; b) il momento magnetico anomalo dell’elettrone; c) la costante di struttura fine α; d) la struttura iperfine dell’idrogeno; e) la struttura fine del positronio; f) il Lamb shift degli atomi muonici; g) il momento magnetico anomalo del muone. Riguardo alla verifica a), a causa di correzioni caratteristiche dell’e. quantistica, alcuni livelli energetici dell’atomo di idrogeno, che altrimenti coinciderebbero, si separano. La separazione dovuta a tali spostamenti (Lamb shift) può essere misurata direttamente osservando il fotone emesso dall’atomo nella transizione dall’uno all’altro livello (fotone la cui frequenza cade nel campo delle microonde). Per es. nel caso dei livelli 2²S_1/2 e 2²P_1/2 i risultati sperimentali più accurati danno valori 1057,8583 (22) MHz, a fronte di previsioni teoriche di 1057,875 (10) MHz. La misura b) riguarda in effetti il rapporto giromagnetico g dell’elettrone, cioè il rapporto fra il momento magnetico intrinseco e lo spin (o momento angolare intrinseco). In base alla teoria di Dirac, nel limite non relativistico, g=2. L’e. quantistica prevede invece un valore leggermente inferiore. Lo scarto relativo dal valore g=2, cioè la grandezza a_e=(g−2)/2 definisce la cosiddetta anomalia del momento magnetico dell’elettrone. Con tecniche estremamente raffinate sono state effettuate misure fra le più precise che siano state confrontate con una previsione teorica, con una discrepanza relativa della misura dell’anomalia inferiore a 4‧10⁻⁸ e di circa 10⁻¹⁴ nella misura del rapporto giromagnetico dell’elettrone.

Fra le verifiche dell’e. quantistica ad alta energia di rilievo sono quelle relative agli urti elastici fra elettroni e positroni (diffusione di Bhabba), all’annichilazione di coppie di leptoni e all’annichilazione in due fotoni.