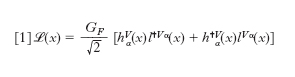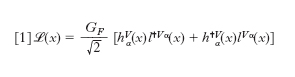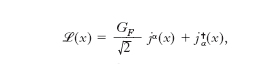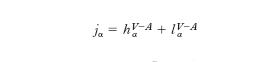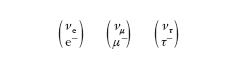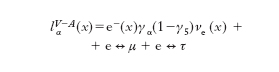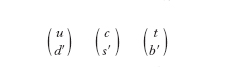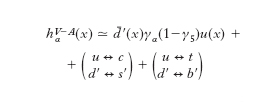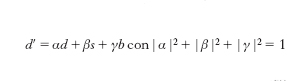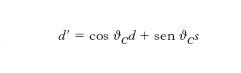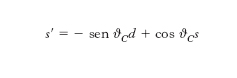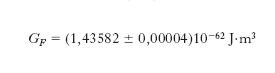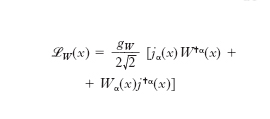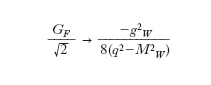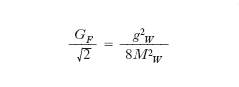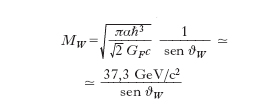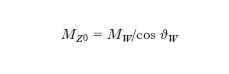deboli, interazioni

tab

Uno dei 4 tipi di interazioni fondamentali tra particelle elementari (forti, elettromagnetiche, d. e gravitazionali) alle quali si possono ricondurre tutti i fenomeni fisici osservati. Derivano il loro nome dall’intensità delle forze corrispondenti, di gran lunga inferiore a quella delle forze forti, che legano i nuclei, e delle forze elettromagnetiche, che legano ai nuclei gli elettroni atomici e molecolari, pur essendo comunque molto più intense delle forze gravitazionali (queste ultime sono completamente trascurabili in fisica atomica, nucleare e subnucleare e importanti solo a livello macroscopico). Mentre le interazioni elettromagnetiche e gravitazionali sono a portata (range) infinita, con intensità decrescenti secondo la legge coulombiana o newtoniana di proporzionalità inversa con il quadrato della distanza, le forze forti dei nuclei e quelle deboli si smorzano esponenzialmente e si manifestano quindi solo entro un range r limitato, la cui scala è determinata dalla massa M del più leggero dei portatori della forza corrispondente, secondo la relazione r ≃ ℏ /Mc, dove ℏ è la costante di Planck ridotta, e c è la velocità della luce nel vuoto. Per le forze nucleari r è determinato dalla massa Mπ del pione pari a circa 140 MeV/c² e r ≃ 10^–13 cm; per le interazioni d. r. ≃ 10^–16 cm, corrispondente a una massa dell’ordine di 100 GeV/c² per i bosoni intermedi portatori delle forze deboli. Le interazioni d. violano un certo numero di simmetrie esattamente rispettate dalle altre interazioni fondamentali, quali la parità P, la coniugazione di carica C, la conservazione dei numeri quantici di ‘flavour’, che distinguono i vari tipi di quark (➔), quali isospin, stranezza, charm, beauty. Proprio il manifestarsi di queste violazioni evidenzia in molti casi la presenza delle interazioni deboli. Anche la violazione molto più limitata che si osserva della simmetria T per inversione di tempo, ovvero la violazione del prodotto CP, si può incorporare entro l’ambito della teoria attuale delle interazioni d. unificate con le elettromagnetiche. Le interazioni d. causano la radioattività beta nei nuclei, i decadimenti (v. tab.) del neutrone libero, degli iperoni, dei pioni carichi, dei mesoni K, degli stati mesonici e barionici più leggeri con charm, beauty ecc. (tutti questi decadimenti di stati altrimenti stabili sono resi possibili dalla non conservazione nelle interazioni d. del flavour) e inoltre i decadimenti dei leptoni carichi più pesanti dell’elettrone (μ^±, τ^±). A reazioni nucleari indotte dalle interazioni d. si deve la copiosa produzione di energia nel Sole e nelle altre stelle. Lo studio delle interazioni d. si è sempre rivelato di estrema importanza per lo sviluppo teorico della fisica delle particelle elementari.

La teoria di Fermi del decadimento beta

fig. 1

fig. 2

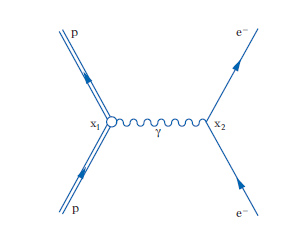
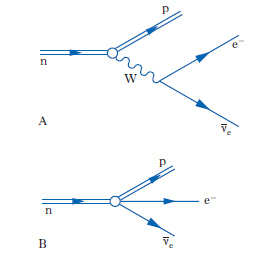
La radioattività beta fu scoperta nel 1896 da H. Becquerel, ma solo dopo il 1930 le conoscenze teoriche, con lo sviluppo della meccanica quantistica e della teoria dei campi, permisero di affrontare il problema di una teoria del decadimento beta, l’unica classe di processi deboli allora noti. Il decadimento beta (β⁻) consiste nella trasformazione di un neutrone, libero o legato in un nucleo (con opportune condizioni per l’energia di legame), in un protone con l’emissione di un elettrone e di un antineutrino: n → p + e⁻ + ν̄_e. Nei nuclei si può anche avere il processo inverso (β⁺): p → n + e⁺ + ν̄_e. Il neutrino (➔), di spin 1/2 e massa nulla o comunque molto piccola, fu appunto introdotto da W. Pauli per garantire che in queste reazioni si conservasse il momento angolare e l’energia. Infatti si osserva uno spettro continuo di energia per l’elettrone, nel centro di massa del neutrone iniziale, e non un’energia fissata come atteso per un decadimento in due corpi finali. Nel 1934 E. Fermi formulò la prima teoria quantitativa del decadimento beta, le cui idee fondamentali, pur in forma largamente estesa e notevolmente modificata, sono tuttora presenti nella moderna teoria delle interazioni deboli. Fermi costruì la sua teoria rifacendosi al modello dell’elettrodinamica quantistica (➔ elettrodinamica), in cui l’interazione tra due cariche, per es. un protone e un elettrone (fig. 1), avviene mediante lo scambio di un fotone, che si accoppia in un punto (x₁) dello spazio-tempo alla corrente elettromagnetica (quadri)vettoriale del protone e in un secondo punto (x₂) alla analoga corrente dell’elettrone. Il raggio di azione infinito della interazione elettromagnetica corrisponde alla massa nulla del fotone. Eliminando in prima approssimazione un bosone intermedio analogo al fotone (approssimazione di raggio d’azione nullo), Fermi descrisse l’interazione d. per il decadimento beta come il prodotto di due correnti (quadri)vettoriali, una adronica e una leptonica, operanti ambedue nello stesso punto dello spazio-tempo (fig. 2). I termini della densità di lagrangiana rilevanti per il decadimento beta risultano quindi della forma

[1] formula

dove h^V_α e l^V_α (il suffisso V sta per vettoriale) indicano le correnti adronica e leptonica rispettivamente, h^✝V_α e l^✝V_α i corrispondenti operatori hermitiani coniugati, x è la coordinata spazio-temporale, α è l’indice di Lorentz e GF è una costante dimensionale d’accoppiamento che prende appunto il nome di costante di Fermi. Nel decadimento β⁻ la corrente adronica induce la transizione n → p mentre la corrente leptonica produce dal vuoto la coppia e⁻ ν̄_e. Si parla quindi di correnti ‘cariche’, in quanto nelle transizioni indotte da ciascuna corrente la carica elettrica varia di una unità, mentre naturalmente nel processo complessivo la carica è conservata. In questo senso la corrente elettromagnetica è invece ‘neutra’ perché l’emissione o l’assorbimento di un fotone non cambiano la carica elettrica. La densità di lagrangiana [1], essendo il prodotto di due correnti (quadri)vettoriali, è invariante per trasformazioni di Lorentz e conserva separatamente P e C. Tuttavia già nel 1936 G. Gamow e E. Teller mostrarono che il termine di Fermi V•V, sufficiente per spiegare le transizioni tra nuclei con il medesimo spin J, certamente non può spiegare i decadimenti beta con incremento di spin ∣ ΔJ ∣ = 1, osservati con velocità di reazione comparabili, per i quali sono necessari termini con correnti assiali o tensoriali.

La teoria V – A

La forma attuale della lagrangiana effettiva per i decadimenti beta e, più in generale, per i processi deboli da corrente carica a basse energie, fu raggiunta solo circa tre decenni più tardi con lo studio di una classe sempre più vasta di processi deboli. La struttura generale rimane fissata nel prodotto di due correnti

[2] formula

dove la corrente debole carica j^α è la somma di una corrente adronica e di una leptonica

[3] formula

La corrente adronica h^V_α^−A e quella leptonica l^V_α^−A sono ambedue sovrapposizioni di un termine vettoriale e di un termine pseudovettoriale o assiale, con comportamento opposto sia sotto P sia sotto C. La struttura della corrente leptonica è identica per i tre doppietti di leptoni (coppie elettrone-neutrino) conosciuti

[4] formula

ed è data da

[5] formula

dove e(x), ν_e(x) indicano i campi spinoriali a quattro componenti per le particelle corrispondenti, γ_α e γ₅ sono le matrici 4×4 di Dirac (Dirac, Paul Adrien Maurice) e con e ↔ μ ed e ↔ τ si sono indicati i termini, del tutto identici, per i doppietti del μ e del τ. Il termine in γ_α è puramente vettoriale mentre il termine in γ_αγ₅ è puramente assiale. Come si vede, questi due termini intervengono con lo stesso peso e con il segno relativo fissato, il che giustifica il suffisso V – A che figura sulle correnti h^V_α ^–A, l^V_α ^–A e il nome di ‘teoria V meno A’ (delle correnti d. cariche) che ricorre di frequente. Il termine elettronico della corrente l^V_α ^–A può dare luogo alle transizioni ν_e e⁺ → 0, ν_e → e^–, 0 → e^–ν̄_e, e⁺ → ν̄_e, mentre le transizioni inverse sono indotte dalla corrente hermitiana coniugata l^✝_α^{V –A}, e analogamente per gli altri termini leptonici. La struttura della corrente carica adronica h^V_α ^–A, espressa in termini dei campi dei costituenti degli adroni, cioè i quark, è ancora del tutto simile a quella di l^V_α ^–A. Si hanno infatti tre doppietti di quark

[6] formula

in completa simmetria con i doppietti leptonici. Ogni doppietto di quark è replicato in 3 ‘colori’. I numeri quantici di colore sono però irrilevanti ai fini delle interazioni d., le quali distinguono solo il flavour, e si possono pertanto ignorare. Nei doppietti [5] d′, s′ e b′ sono delle sovrapposizioni lineari unitarie dei campi dei quark d, s e b, i quali ultimi hanno massa definita. A ogni doppietto corrisponde un termine in h^V_α ^–A della stessa forma che nel caso leptonico

[7] formula

In questo caso le transizioni indotte dal primo termine sono ud̅′ → 0, u → d′, 0 → d′ū, d̅′ → ū, mentre le transizioni inverse derivano dal termine corrispondente in h^✝_α^{V –A}. Una proprietà fisica fondamentale delle interazioni d. che è contenuta nella formulazione ora enunciata è la violazione della parità e della coniugazione di carica C. Infatti nel prodotto di due correnti (V−A) ∙ (V−A) si hanno sia termini del tipo VV + AA, scalari e con C positiva, che termini del tipo VA + AV, pseudoscalari e con C negativa. I primi termini conservano P e C, mentre i secondi violano entrambe, pur conservando il prodotto CP. La violazione è massimale in quanto il coefficiente dei termini che rompono tali simmetrie è in modulo uguale a quello dei termini che le preservano. La possibilità della non conservazione della parità nelle interazioni d. fu considerata da T.D. Lee e C.N. Yang nel 1957 che così risolsero in modo corretto il problema posto dall’esistenza dei decadimenti del K⁺ in 2π e in 3π: K⁺ → π⁺π⁰, K⁺ → π⁺π π⁰. Dal fatto che il K⁺ ha spin zero e che i π sono particelle pseudoscalari segue che gli stati finali 2π e 3π hanno parità opposte. Lee e Yang osservarono che non esistevano prove sperimentali della conservazione di P nelle interazioni deboli. Suggerirono quindi che si trattasse di un unico tipo di particella che decade nei due modi con violazione di parità (anziché ammettere l’esistenza di due particelle diverse con uguale massa e vita media) e indicarono, infine, varie esperienze per accertare in modo diretto la violazione di P. Queste esperienze, eseguite poco dopo, mostrarono che P è effettivamente violata sia nel decadimento beta nucleare (C.S. Wu et al., 1957) sia nei decadimenti del μ e degli iperoni. Similmente la violazione massimale di C fu stabilita sperimentalmente nel decadimento del μ e dalla misura di una polarizzazione all’incirca opposta per leptoni e antileptoni prodotti nei processi da corrente carica. La struttura V – A delle correnti cariche comporta infatti che, nel limite di massa nulla, hanno interazioni d. da correnti cariche solo i fermioni fondamentali (quark e leptoni) con elicità negativa e gli antifermioni con elicità positiva, essendo l’elicità la componente dello spin nella direzione del moto. In questo limite la teoria V – A ha una struttura chirale, in quanto solo le particelle con definita chiralità possono interagire. Poiché l’applicazione di P cambia segno all’elicità e quella di C muta fermioni in antifermioni con uguale elicità, si ottiene subito che la proprietà suddetta delle interazioni d. rappresenta una chiara violazione di P e C mentre è compatibile con l’invarianza sotto il prodotto CP. Il limite di massa nulla potrebbe essere realizzato esattamente per i neutrini, e in effetti si osservano esclusivamente neutrini con elicità negativa e antineutrini con elicità positiva.

Un’altra delle proprietà fondamentali delle interazioni d. è l’universalità. Tutti i fermioni fondamentali (quark e leptoni) hanno interazioni d. e inoltre abbiamo visto che nelle correnti deboli cariche i termini ν̄_ee^–, ν_μμ^–, ν_ττ^–, ūd′, c̄s′ e t̄b′ appaiono in modo perfettamente simmetrico. Si hanno quindi tante interazioni con un unico accoppiamento universale. Nel caso dei quark però l’intensità complessiva di ogni quark di tipo ‘up’ (carica + 2/3) è suddivisa tra tutti i quark di tipo ‘down’ (carica – 1/3). Così per es.

[8] formula

e analogamente per s′ e b′, queste ultime combinazioni essendo ortogonali tra loro e a d′. Si ha quindi che la somma delle probabilità di transizione dal quark u ai quark d, s e b, con massa definita, è uguale alla probabilità della singola transizione ῡ_ee^–, e analogamente negli altri casi. In particolare, se consideriamo il settore dei quark leggeri u, d, s e trascuriamo l’accoppiamento di u a ogni quark più pesante di s, approssimazione che si rivela empiricamente molto accurata, d′ assume la forma

[9] formula

originariamente introdotta nel 1963 da N. Cabibbo, al quale si deve la formulazione corretta dell’universalità delle interazioni d., nei termini ora descritti. ϑ_C è detto appunto angolo di Cabibbo e sperimentalmente risulta ϑ_C ≃ 13°, ovvero sen ϑ_C ≃ 0,224. La combinazione ortogonale a d′

[10] formula

all’epoca della formulazione originale della teoria di Cabibbo appariva disaccoppiata, mentre oggi sappiamo che interagisce con il quark con charm c. L’esistenza di questo mescolamento (mixing) nel caso dei quark deriva dal fatto che hanno masse differenti e che gli stati selezionati dall’accoppiamento debole non coincidono con gli stati a massa definita. La stessa complicazione sarebbe presente anche nel settore leptonico se le masse dei neutrini fossero differenti tra loro, in particolare non tutte nulle, e la eventuale esistenza di un mixing leptonico potrebbe essere dimostrata rivelando le cosiddette oscillazioni dei neutrini.

Processi da correnti cariche

Dallo sviluppo del prodotto delle correnti cariche nell’equazione [2], tenuto conto delle equazioni [3, 4, 6], si ottengono le tre classi dei processi puramente leptonici, semileptonici e non leptonici che corrispondono ai termini ll⁺, hl⁺ + lh⁺ e hh⁺ rispettivamente.

Processi puramente leptonici

Sono quelli per i quali lo studio degli effetti delle interazioni d. è in linea di principio più semplice in quanto i leptoni (➔ leptone) non hanno interazioni forti che quanto meno complicano l’analisi e i cui effetti sono spesso difficili da calcolare. Di questa classe il processo di gran lunga più studiato sperimentalmente è il decadimento del μ: μ^∓ → e^∓ ∓ ν_e ± ν_μ, dove la notazione −ν indica qui e nel seguito +ν̄, cioè la presenza di un antineutrino. Poiché questo modo di decadere del μ è l’unico apprezzabile, confrontando il valore sperimentale della vita media con il calcolo teorico di questa stessa quantità, ivi comprese le correzioni radiative dovute alle interazioni elettromagnetiche dei leptoni carichi, si ottiene la migliore determinazione della costante di Fermi

[11] formula

Altri notevoli processi puramente leptonici da correnti cariche sono i decadimenti del τ (τ^± → e^± ± ν_e ∓ ν_τ, τ^± → μ^± ± ν_μ ∓ ν_τ) e le reazioni elettroneneutrino: e^– + ν_e → e^– + ν_e, e^– + ν̄_e → e^– + ν̄_e alle quali ultime contribuiscono anche le correnti neutre.

Processi semileptonici

Rientra in questa categoria un grande numero di decadimenti di mesoni e barioni (in particolare i decadimenti beta già discussi) e i processi di diffusione leptone-adrone.

Processi non leptonici

Sono i più complessi da analizzare in quanto gli effetti delle interazioni forti sono pienamente operanti in questo caso. I processi più studiati sono i decadimenti con violazione di stranezza dei K in pioni (K → 2π, 3π) e degli iperoni, che sono spiegati nella teoria di Cabibbo dal prodotto di una corrente u ↔ d, ū ↔ d̅ con una corrente s ↔ u, s̄ ↔ ū con accoppiamento complessivo proporzionale a cos ϑ_C sen ϑ_C e regole di selezione ∣ ΔS ∣ =1, ΔI = 1/2, 3/2 (dove I è l’isospin). Di particolare importanza sono i decadimenti K⁰_L → 2π, non consentiti da interazioni che conservano CP. Nel 1964 J.A. Christenson e collaboratori scoprirono invece che tali decadimenti in effetti avvengono, seppure con probabilità relativa molto piccola, dell’ordine di 10⁻³. Ne consegue che la conservazione di CP è violata e che gli stati a vita media definita K⁰_S e K⁰_L non sono autostati di CP. Attualmente si attribuisce la violazione di CP a una proprietà della matrice di mixing dei quark già descritta a proposito della universalità.

Teoria unificata delle interazioni elettrodeboli

Verso la fine degli anni 1960 il problema di una descrizione fenomenologica dei processi da interazioni d. fino ad allora conosciuti (lasciando da parte la violazione di CP come un effetto dovuto a un’interazione ‘superdebole’ ulteriore) poteva considerarsi risolto dalla interazione ottenuta come prodotto locale di due correnti V – A. Era però chiaro che la teoria esistente non poteva considerarsi compiuta a livello fondamentale. Infatti i risultati interessanti e in accordo con l’esperienza si ottenevano trattando l’interazione all’ordine più basso perturbativo, ignorando i termini di ordine superiore nello sviluppo, i quali d’altra parte erano privi di senso perché infiniti. Il problema che si poneva era dunque quello di riottenere i risultati fisici corretti della teoria fenomenologica a partire da una teoria di campo ben definita, in particolare con un comportamento meno singolare ad alti momenti trasferiti, che corrispondono a piccole distanze. Un primo passo in questa direzione fu quindi l’introduzione di un range finito per le interazioni d. in quanto il grado di singolarità a piccole distanze della teoria diminuisce se il prodotto di due correnti nello stesso punto è sostituito con l’emissione e l’assorbimento in due punti diversi di un bosone vettoriale carico W⁺ (o la sua antiparticella W^–) accoppiato alla corrente debole (fig. 2), in analogia allo scambio di un fotone tra due particelle cariche nell’interazione elettromagnetica. L’interazione fondamentale tra il W^±, detto bosone intermedio debole, e la corrente debole carica j_α(x), definita nell’equazione [3], diviene

[12] formula

dove g_W è una nuova costante adimensionale. All’ordine più basso della teoria delle perturbazioni i risultati dedotti da questa nuova densità di lagrangiana coincidono con i precedenti a meno della sostituzione (in unità ℏ = c = 1)

[13] formula

dove q_a è il quadrimomento trasferito da una corrente all’altra (q² = q_αq^α) e M_W è la massa del W^±. Per piccoli valori di q² (q² ≪ M²_W) si riottengono i risultati della teoria basata sul prodotto di due correnti, con l’identificazione

[14] formula

Ad alti momenti trasferiti (q² ≫ M²_W) si ottiene invece un andamento decrescente come –g²_W/8q² che rende la teoria più convergente per q² → ∞. La compatibilità con i risultati sperimentali richiedeva che M_W ≳ 20 GeV/c². L’introduzione dei W^± pur migliorando il grado di convergenza della teoria non è però di per sé sufficiente a renderla finita. Nel caso dell’elettromagnetismo la proprietà ulteriore che rende la teoria rinormalizzabile è l’invarianza di gauge, cioè l’invarianza sotto un gruppo di trasformazioni i cui parametri sono diversi da punto a punto dello spazio-tempo. L’osservazione fondamentale che le correnti deboli cariche e la corrente elettromagnetica sono componenti di uno stesso multipletto di isospin o di SU(3) (CVC, algebra delle correnti e relative verifiche sperimentali) conduce naturalmente a considerare l’estensione della simmetria di gauge a includere anche il settore debole e la costruzione di una teoria di gauge unificata delle interazioni elettromagnetiche e deboli. Tali tentativi, iniziati già alla fine degli anni 1950, urtarono da principio contro due ordini di difficoltà. La prima difficoltà consisteva nella dissimmetria tra la massa nulla del fotone e l’elevata massa dei W^± che rendeva problematica la identificazione di queste ultime particelle con dei bosoni di gauge (che hanno necessariamente massa nulla se la simmetria di gauge è soddisfatta). La seconda nella apparente assenza di una corrente debole neutra, anche essa accoppiata a un bosone di gauge Z⁰ di massa elevata, essenzialmente inevitabile per il completamento della struttura algebrica di una teoria di gauge. D’altra parte la violazione di P e C, presente nelle interazioni d. e non in quelle elettromagnetiche, poteva essere incorporata nella teoria dotando il gruppo di gauge di una struttura chirale, cioè facendo trasformare in modo diverso i fermioni con elicità positiva e negativa (di massa nulla nel limite di simmetria esatta). Il primo tipo di difficoltà, di natura tecnica, fu superato con la formulazione delle teorie con rottura spontanea di simmetria e del ‘meccanismo di Higgs’ (bosone) che permette, in una teoria di gauge, di rimuovere i bosoni di Goldstone a massa nulla necessariamente associati alla rottura spontanea di simmetria e non osservati e, allo stesso tempo, di dotare di massa i bosoni di gauge con i numeri quantici corrispondenti ai generatori delle simmetrie rotte e i fermioni fondamentali, senza distruggere la rinormalizzabilità della teoria (G. ’t Hooft, 1971). Questi progressi furono mutuati dalla fisica dei fenomeni critici (critico) e in generale dalla teoria dei sistemi a molti corpi. Si giunse così alla formulazione del quadro generale della teoria attuale delle interazioni elettrodeboli (S. Weinberg, 1967, A. Salam, 1968) basato sul gruppo di gauge SU(2) ⊗ U(1) già considerato in precedenza nel limite di simmetria esatta (S. Glashow, 1961). Tale teoria sembrava però smentita dall’esperimento per l’assenza della corrente debole neutra, che con i quark allora conosciuti avrebbe necessariamente dovuto possedere delle componenti con violazione di stranezza, facili da rivelare ma di fatto non osservate. La soluzione a questo problema fu trovata con l’introduzione di un quarto tipo di quark, con un nuovo numero quantico di flavour, detto charm (S. Glashow, J. Iliopoulos, L. Maiani, 1970) che, accoppiato nella corrente debole carica alla combinazione s′ nell’equazione [8], viene a rimuovere in modo naturale le componenti con ΔS≠0 della corrente neutra, pur rimanendo ferma la predizione di una corrente neutra senza violazione di stranezza. Finalmente la scoperta della corrente neutra al CERN, il laboratorio europeo di Ginevra, nel 1973 e del charm a Brookhaven e SLAC (Stanford) negli Stati Uniti, nel 1974, posero la teoria su solide basi sperimentali, poi progressivamente consolidate dalla verifica sperimentale degli accoppiamenti della corrente neutra ai quark e ai leptoni in accordo con le previsioni della teoria. Nella teoria di Weinberg-Salam le masse dei bosoni intermedi W^± e Z⁰ e la forma della corrente debole neutra sono pienamente determinate in funzione di un solo parametro, l’angolo ϑW, definito dalla relazione tg ϑW = g′/g, dove g e g′ sono le costanti di accoppiamento relative ai gruppi di gauge SU(2) e U(1) rispettivamente. Per i W^± si ottiene, a meno di piccole correzioni radiative,

[15] formule(

dove α è la costante di struttura fine), mentre per lo Z⁰, nel caso di massima semplicità corrispondente a bosoni di Higgs doppietti di SU(2), si ha

[16] formula

Da varie esperienze si ottiene sen² ϑ_W = 0,226 ± 0,010; ne consegue che M_W ≃ 80 GeV/c² e M_Z⁰ ≃ 90 GeV/c². La corrente neutra risulta la combinazione di una corrente V – A e della corrente elettromagnetica che è puramente vettoriale. Gli esperimenti sui processi deboli da corrente neutra permettono di misurare non solo il valore di sen² ϑ_W già riportato, ma anche il valore del rapporto ρ = M_W²/M_Z²₀ cos² ϑ_W determina l’intensità della interazione debole da corrente neutra. Esso risulta uguale a uno, entro qualche per cento, in accordo con la predizione teorica, fornendo così una conferma indiretta del meccanismo di Higgs per la generazione delle masse dei bosoni intermedi. Dati sperimentali sono stati ottenuti in un gran numero di esperimenti relativi a diversi processi. Tra i processi puramente leptonici sono importanti le difficili misure delle reazioni di diffusione elastica ± ν_μ + e^– → ± ν_μ + e^– che sono indotte unicamente dalla corrente neutra poiché la transizione ν_μ ↔ e^– non è presente tra i termini di corrente carica. Diversa è la situazione dei processi ± ν_e + e^– → ± ν_e + e^– ai quali contribuiscono sia le correnti cariche sia la corrente neutra. I processi semileptonici sono quelli per i quali esistono i dati più abbondanti. Vanno ricordati in particolare i processi inclusivi ± ν_μ + N → ± ν_μ + X che in effetti hanno portato alla scoperta della corrente neutra. Questi dati, insieme a quelli relativi ad alcuni specifici canali X, permettono di risalire agli accoppiamenti di corrente neutra dei singoli quark leggeri. Molto importante è stato anche l’esperimento, eseguito a SLAC, che ha rivelato la minuscola violazione di parità indotta dalla corrente debole neutra nel processo, dominato dalla interazione elettromagnetica, su deuterio e^– + D → e^– + X; l’effetto è stato misurato anche su protone, seppure con minore precisione. La quantità non nulla che dimostra la violazione di parità è la variazione percentuale, dell’ordine di 10^–4, tra le sezioni d’urto da elettroni con elicità positiva oppure negativa. L’interazione tra elettroni e quark mediata dallo Z⁰ è anche responsabile di violazioni di parità in fisica atomica che sono però così piccole da poter essere osservate, con difficoltà, solo in casi particolarmente favorevoli. Alcune esperienze volte a questo scopo hanno in effetti misurato delle violazioni di parità, in buon accordo con le previsioni teoriche, pur nei limiti non stringenti degli errori sperimentali. La rivelazione di effetti da corrente neutra in processi non leptonici, infine, sarebbe in linea di principio possibile, ma è difficile in pratica. La verifica ultima della teoria si è avuta (1983) al CERN, grazie alla scoperta da parte di C. Rubbia e collaboratori dello Z⁰ e dei W^± con le masse previste dalla teoria stessa. Dopo di ciò, la struttura basata sulla simmetria di gauge spontaneamente rotta può dirsi acquisita, anche se, per il completamento del quadro, è ancora necessario dimostrare sperimentalmente l’esistenza di (almeno) un bosone di Higgs neutro di spin zero, per il quale tuttavia non esiste una predizione di massa. Lo schema teorico così formulato dovrebbe estendere la sua validità almeno fino a energie dell’ordine di 300-1000 GeV. Al di là di questo orizzonte, fenomeni nuovi potrebbero manifestarsi con la scoperta di nuovi gradi di libertà, quali nuovi bosoni di gauge, subcostituenti dei quark e dei leptoni (preoni) o anche dei bosoni di Higgs, o quali gli analoghi supersimmetrici dei campi noti (le supersimmetrie stabiliscono una corrispondenza biunivoca tra i gradi di libertà bosonici e fermionici) ecc. Rimangono infatti aperti alcuni problemi fondamentali, primo fra tutti appunto quello della reale natura del meccanismo di rottura spontanea della simmetria di gauge con una comprensione della matrice di massa dei fermioni e in generale dei molti parametri indeterminati che ancora sono presenti nella teoria attuale. È anche però intuibile che la risoluzione di tali problemi vada differita fino a energie enormi, dell’ordine di 10¹⁹ GeV, alle quali la gravitazione comincia ad avere un ruolo nella fisica subnucleare. Sarebbe in questo caso forse possibile un’ulteriore preliminare unificazione delle interazioni elettrodeboli e forti (grande unificazione) in una teoria di gauge più vasta ma di uguale struttura (basata su un unico gruppo di gauge più grande), a energie dell’ordine di 10¹⁴-10¹⁵ GeV, secondo le linee di un certo numero di modelli concreti che sono stati costruiti e studiati nel corso degli ultimi anni.