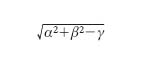parametro

In matematica, variabile indipendente o coordinata suscettibile di assumere tutti i valori reali o complessi (p. reale o p. complesso) o anche, più in generale, valori che si rappresentano nei punti di un insieme aperto della retta reale o del piano complesso. Così, per es., si dicono p. i 3 coefficienti reali α, β, γ dai quali dipende una circonferenza che abbia come centro (α, β) e il cui raggio sia

la sua equazione è allora x²+y²−2αx−2βy+γ = 0. L’equazione di questa stessa circonferenza può anche essere scritta nella forma: ax²+ay²+bx+cy+d = 0 ponendo b/a = −2α, c/a = −2β, d/a = γ. Si dirà che l’equazione di una circonferenza in un piano dipende da 3 p. essenziali (per es., α, β, γ): il che vuol dire che a ogni terna (α, β, γ), tale che α²+β²−γ sia positivo, corrisponde una circonferenza e viceversa. Si dirà invece che i 4 p. a, b, c, d non sono tutti essenziali perché alle infinite quaterne (ka, kb, kc, kd) tra loro proporzionali al variare di k, corrisponde una sola circonferenza: ciò vuol dire che si può scegliere ad arbitrio il valore di un p., ponendo, per es., a = 1, o anche che bisogna considerare, per avere una volta e una soltanto tutte le circonferenze di un piano, solo i rapporti di 3 p. al quarto. Si dice poi che un ente, i cui elementi si possono rappresentare con l’aiuto di n p. essenziali e indipendenti, costituisce una totalità di ‘infinito a n’ elementi (simbolo: ∞ⁿ). P. viene perciò a essere, come si è detto, sinonimo di coordinata (➔ coordinate).