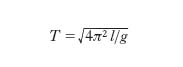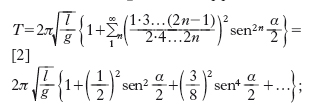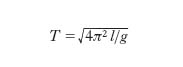pendolo
Solido girevole intorno a un asse fisso non passante per il centro di massa (generalmente orizzontale) e soggetto soltanto all’azione del peso; fra i vari moti di cui un p. è suscettibile ha particolare interesse il moto oscillatorio. Diversi sono, in relazione alle sue applicazioni, i modi di realizzare un p.: nella forma più comune esso è costituito da un’asticella incernierata a un estremo e portante all’altro una massa (massa pendolare).
Cenni storici
La particolare importanza scientifica e pratica del p. fu intuita da G. Galilei, il quale riconobbe che il periodo di oscillazione di palline sospese per mezzo di fili è proporzionale alla radice quadrata della lunghezza del p. e non dipende dalla massa della pallina oscillante; egli ritenne che tale legge restasse valida per una qualsiasi ampiezza di oscillazione, mentre, come si dirà, l’isocronismo sussiste soltanto entro i limiti delle piccole oscillazioni. La teoria rigorosa e completa del p. si deve (1673) a C. Huygens, che stabilì la legge di equivalenza di un p. composto a un p. semplice e precisò, con l’introduzione di quelle grandezze che saranno poi dette momenti d’inerzia, in qual modo influiscano nella rotazione d’un solido intorno a un asse le masse del solido e le loro distanze dall’asse.
Il p. semplice
Il p. semplice è costituito da una massa puntiforme soggetta al solo peso, vincolata a muoversi senza attrito su una circonferenza fissa posta in un piano verticale. Com’è evidente, nessun p. effettivo può attuare rigorosamente le condizioni suddette, quindi il p. semplice (fig. 1)
va considerato come una schematizzazione matematica di dispositivi più complessi; e appunto per questo motivo ha anche la qualifica di p. matematico. Lo studio matematico dei moti del p. non ha in generale carattere elementare, benché l’impostazione del problema sia assai semplice. Essa parte dalla legge fondamentale della dinamica; indicando con m la massa del punto materiale P, con l la lunghezza del p. (cioè il raggio della circonferenza traiettoria c), con g l’accelerazione di gravità e con ϑ l’anomalia variabile di P, poiché si suppone il vincolo privo di attrito, la componente tangenziale della forza agente su P si riduce a −mg senϑ, componente del peso di P valutata secondo la tangente s a c orientata in verso concorde al verso assunto come positivo per la misura dell’angolo ϑ. Poiché, d’altra parte, l’accelerazione tangenziale vale ld2ϑ/dt2, proiettando l’equazione fondamentale della dinamica sulla tangente suddetta, si ha
[1] formula
Di conseguenza le caratteristiche del moto del p. si deducono dall’integrazione della [1], ove si fissino posizione e velocità iniziali di P. Assunto come istante iniziale un istante in cui la massa pendolare si trova in P0, si hanno tre tipi di moto a seconda del valore della velocità iniziale v0: a) oscillatorio, se v0<2(lg)1/2; b) a meta asintotica, se v0=2(lg)1/2; c) rotatorio progressivo, se v0>2(lg)1/2. Nel primo caso il moto si svolge, con andamento periodico, fra due posizioni estreme E, E′, simmetriche rispetto alla verticale condotta per il centro O della circonferenza c cui appartiene la traiettoria del pendolo. Assunti gli assi di riferimento x, y come in fig. 1,
i due punti E, E′ si possono ottenere come intersezioni di c con la retta r di equazione x=l−v02/(2g). Ciò si può dedurre con considerazioni energetiche. Assumendo infatti nulla l’energia potenziale in P0, l’energia cinetica in quel punto, mv02/(2, sarà totalmente trasformata in energia potenziale nei punti E, E′, e tale energia sarà mg(l−x), dove x è, in valore e segno, l’ordinata x di E, E′; uguagliando le espressioni delle due forme di energia si ottiene appunto l−x=v02/(2g). L’angolo α≡EÔP0 è l’ampiezza di oscillazione. Il periodo di oscillazione, cioè il tempo impiegato per ritornare nello stesso punto con la medesima velocità, cioè per fare un’oscillazione completa, si può esprimere mediante il seguente sviluppo in serie:
[2] formula;
esso è dunque generalmente dipendente dall’ampiezza α. Nel moto a meta asintotica, il punto, partendo da P0 con velocità v0=2(gl)1/2, si approssima costantemente e indefinitamente alla posizione H senza mai raggiungerla; questo moto può considerarsi come un caso limite sia del moto oscillatorio, sia del moto rotatorio progressivo (che ha esso pure andamento periodico). Se il moto di un p. è oscillatorio e l’ampiezza di oscillazione è così piccola da poterla confondere con il suo seno (senα∼α), allora si è nel caso elementare delle piccole oscillazioni, dette anche oscillazioni armoniche per il fatto che la [1] si riduce all’equazione del moto armonico (d2ϑ/dt2=gϑ/l) e l’anomalia varia col tempo secondo una legge del tipo ϑ=Acos(ωt+B), dove ω=(g/l)1/2 e A, B sono costanti d’integrazione i cui valori dipendono dalle condizioni iniziali. Il periodo, come può ricavarsi direttamente e come del resto risulta dalla [2] non appena si suppongano trascurabili rispetto all’unità tutte le potenze di sen(α/2), vale
[3] formula,
esso risulta cioè, diversamente da quanto si verifica per il generico moto oscillatorio del p., indipendente dall’ampiezza di oscillazione (legge dell’isocronismo). Nel caso delle piccole oscillazioni, il modello fisico cui abitualmente si ricorre per rappresentare il p. semplice è costituito da una pallina sospesa a un filo inestensibile e privo di massa.
Il p. composto
Alla stessa trattazione matematica del problema del p. semplice si riconduce quella del p. composto o p. fisico. Un p. composto è un corpo, soggetto al solo peso, girevole senz’attrito attorno a un asse fisso orizzontale non passante per il centro di massa detto asse di sospensione. Precisamente, un p. composto è dinamicamente equivalente (nel senso che la sua dinamica è retta dalle stesse equazioni) a un p. semplice di lunghezza
[4] formula,
dove I è il momento d’inerzia del p. rispetto all’asse a di sospensione, I0 il suo momento d’inerzia rispetto alla parallela passante per il centro di massa a0, m la sua massa, δ la distanza del suo centro di massa G da a. In altre parole, a parità di condizioni iniziali un p. composto si muove come si muoverebbe un p. semplice di lunghezza l, la quale dicesi perciò lunghezza ridotta o equivalente del p. composto. Tale lunghezza risulta, come si vede dalla [4], sempre maggiore della distanza δ di G da a; la parallela a′ all’asse di sospensione a distanza l da esso si chiama asse di oscillazione; le proiezioni di G su a e su a′ si chiamano rispettivamente centro di sospensione S e centro di oscillazione O. I due assi a e a′ si dicono coniugati per il motivo che, se si assume come asse di sospensione a′, il nuovo asse di oscillazione viene a coincidere con a (legge di reversibilità del p.). L’equivalenza dinamica fra un p. composto e un p. semplice permette senz’altro di affermare che è valida anche per le piccole oscillazioni del p. composto la legge dell’isocronismo. Il periodo di tali oscillazioni è quindi ancora dato dalla [3] dove per l si intenda la lunghezza ridotta data dalla [4]. La misurazione del periodo delle piccole oscillazioni di un p. del quale siano note le proprietà strutturali consente fra l’altro di risalire al valore di g (p. geodetico). Inversamente, noto che sia insieme a T, m e δ il valore di g, la [3] e la [4] possono essere utilizzate per la determinazione sperimentale di momenti d’inerzia. In talune applicazioni, per es. negli orologi a p., i p. vengono costruiti in modo che se ne possa variare entro certi limiti la lunghezza ridotta e quindi il periodo delle oscillazioni isocrone.
Il p. balistico
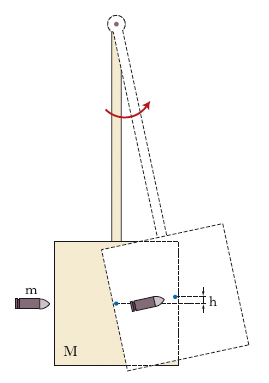
Il p. balistico è un dispositivo usato per la misurazione della velocità iniziale di un proiettile lanciato da una bocca da fuoco. È un robusto p. composto (fig. 2) di massa M costituito da materiale anelastico (per e. piombo) e destinato a ricevere il proiettile, di massa m, che si affonda in esso senza rimbalzare. Misurando la massima altezza h a cui si solleva il centro di massa del p. in conseguenza dell’impulso ricevuto (o, ciò che è lo stesso, l’ampiezza di oscillazione), la velocità del proiettile si determina con la formula v=(M/m)(2gh)1/2 essendo g il modulo del vettore accelerazione di gravità.
Il p. cicloidale
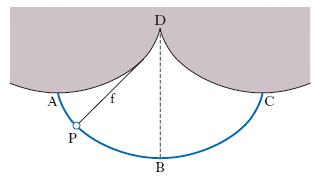
Il p. cicloidale è costituito da un punto materiale soggetto soltanto al peso proprio, vincolato a muoversi senz’attrito su una cicloide contenuta in un piano verticale (fig. 3). Il p. cicloidale è stato considerato per la prima volta da C. Huygens, il quale ha anche suggerito un’elegante maniera di realizzarlo. Poiché l’evoluta di una cicloide è una cicloide uguale, materializzando l’arco di cicloide ADC mediante una superficie cilindrica rigida a generatrici normali al piano della figura e obbligando un filo flessibile e inestensibile f di lunghezza uguale a quella dell’arco DA, fissato per un estremo nella cuspide D, a disporsi sull’arco DA, l’altro estremo P del filo percorre l’arco BA di una cicloide ABC uguale alla precedente: soluzione più teorica che pratica per le difficoltà che incontrerebbe la sua realizzazione.
Per il p. semplice, cioè per il p. circolare, sono, come è noto, isocrone soltanto le piccole oscillazioni; per il p. cicloidale tutte le oscillazioni sono rigorosamente isocrone, cioè il loro periodo risulta esattamente indipendente dalla loro ampiezza e anche dalla posizione iniziale del punto, ciò che si esprime dicendo che il p. cicloidale è tautocrono. Si dimostra che la cicloide è l’unica linea sulla quale un punto pesante, in assenza di attrito, si possa muovere di moto tautocrono; che essa è inoltre brachistocrona, che cioè la traiettoria per la quale risulta minima la durata del percorso tra una posizione A e una posizione B di un medesimo piano verticale è costituita da un arco di cicloide che ha la cuspide in A, la concavità rivolta verso l’alto e il punto più basso in B.
Il p. compensato
Il p. compensato è un p. composto costruito in modo tale che la sua lunghezza, e quindi il suo periodo d’oscillazione, rimanga sensibilmente costante al variare della temperatura ambiente. Ottimi p. compensati si ottengono adottando per l’asta un materiale a bassissimo coefficiente di dilatazione termica, per esempio la lega invar.
Il p. di Foucault
Il p. di Foucault è un p. di grande lunghezza che sia fatto oscillare in un punto qualunque della superficie terrestre, abbandonandolo a sé senza velocità iniziale dopo averlo un poco spostato dalla sua posizione di equilibrio. Se la Terra fosse ferma, le successive oscillazioni si vedrebbero avvenire tutte nello stesso piano verticale; viceversa il piano di oscillazione ruota uniformemente intorno alla verticale del luogo, sicché l’esperienza costituisce una delle prove più convincenti della rotazione della Terra. L. Foucault per primo realizzò l’esperimento nel 1851, mediante un p. di 67 m di lunghezza e con una massa oscillante di 28 kg sospeso alla cupola del Panthéon di Parigi, spiegandone chiaramente il significato sulla base della teoria sviluppata da S.-D. Poisson nel 1838. Il valore della velocità angolare del piano risulta uguale al prodotto della velocità angolare terrestre per il seno della latitudine del luogo di osservazione, in modo che in particolare ai poli essa coincide con la velocità angolare terrestre e all’equatore si annulla.
Il p. geodetico
Il p. geodetico (o p. gravimetrico) è uno strumento usato per la misurazione assoluta o relativa dell’accelerazione di gravità terrestre g (➔ gravimetria) prima dell’introduzione del gravimetro a caduta libera e dei gravimetri differenziali. Consta essenzialmente di un p. composto di cui si possa misurare con grande precisione il periodo
delle piccole oscillazioni, dove l è la lunghezza ridotta del p. stesso. Supponendo di conoscere l, occorre misurare T con un errore percentuale dell’ordine di 10–7 (raggiungibile eseguendo la misura di T su un grande numero di oscillazioni) per avere g con l’approssimazione di 10–6 m/s2.
P. multiplo Apparato gravimetrico costituito da più p. composti identici disposti in modo da eliminare o almeno ridurre l’influenza di eventuali oscillazioni del supporto sulla misurazione di T. A seconda del numero dei p. prende il nome di bipendolo, tripendolo, quadripendolo geodetico, ed è usato specialmente per misurazioni relative di g. Il prototipo di tali apparati è il quadripendolo di R. von Sterneck.
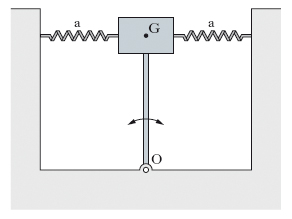
Il p. invertito
Il p. invertito è un p. composto (fig. 4) montato in modo che il baricentro G cada al disopra del centro di oscillazione O, invertendosi così, rispetto a un ordinario p. composto, le reciproche posizioni di G e O. La posizione più alta di G corrisponde a una posizione di equilibrio instabile del p., ma disponendo opportunamente delle molle antagoniste a si può ottenere che il p. oscilli attorno a tale posizione e con periodo più lungo di quello corrispondente alle piccole oscillazioni del p. attorno alla sua posizione di equilibrio stabile. Il valore del periodo è in relazione alle caratteristiche strutturali delle molle.
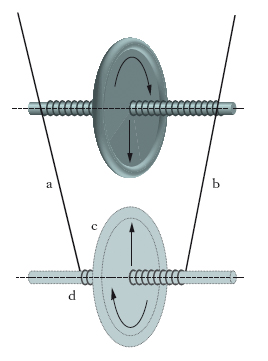
Il p. di Maxwell
Il p. di Maxwell è un dispositivo per esperienze dinamiche che mette in rilievo l’effetto dell’energia cinetica di rotazione e che viene chiamato p. soltanto in senso estensivo; esso è costituito (fig. 5) da una ruota c sospesa mediante due fili a, b avvolti in verso concorde sul suo asse d col quale la ruota è resa solidale. La ruota, abbandonata a se stessa, sotto l’azione del suo peso, prende a scendere e contemporaneamente, mentre il filo si svolge, a ruotare. Quando i fili sono completamente svolti, la discesa si arresta; ma per l’energia cinetica acquistata la ruota seguita a girare, i fili si riavvolgono in verso opposto al precedente, sull’asse, la ruota prende a salire. In assenza di attrito, per la reversibilità del fenomeno, essa ritornerebbe esattamente al livello dal quale aveva iniziato la discesa.
Il p. di torsione e il p. magnetico
Il p. di torsione è costituito da una massetta sospesa a un filo verticale sottile, che, spostata dalla posizione di equilibrio (in cui è nulla la torsione del filo), viene a essa richiamata dalla coppia di torsione della sospensione, oscillando permanentemente (se l’effetto degli attriti è trascurabile) attorno a tale posizione; essendo il momento della coppia di richiamo proporzionale all’angolo di torsione per un largo intervallo di valori di tale angolo, il periodo delle oscillazioni risulta praticamente indipendente dalla loro ampiezza.
Il p. magnetico è un p. di torsione in cui la massetta è costituita da un magnete; in tal caso la coppia di richiamo comprende, oltre alla coppia di torsione, anche la coppia dovuta alla componente dei campi magnetici esterni nel piano in cui oscilla il magnete, e perciò il periodo d’oscillazione dipende dall’intensità di detta componente. È un p. magnetico il magnetometro per la determinazione della componente orizzontale del campo magnetico terrestre col metodo di Gauss-Lamont.
Pendolino elettrico Piccolo p. la cui massa, costituita da una pallina di sughero o di midollo di sambuco, è sospesa mediante un filo di seta a un supporto isolante. Per la sua leggerezza e capacità di elettrizzarsi si presta allo studio dei fenomeni elettrostatici elementari.