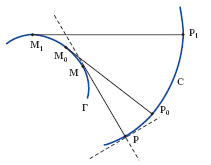
evoluta
In geometria si chiama e. (o sviluppata) di una curva piana C la curva Γ, luogo geometrico dei centri di curvatura dei punti di C; si dice allora che la curva C è una evolvente (o sviluppante) di Γ. Essa può anche definirsi come inviluppo delle normali a C; se infatti (come in fig.) P è un punto generico di C ed M il relativo centro di curvatura, la retta PM, normale a C in P, risulta tangente all’e. in M.
Siano ora P0 e P1 due punti di C, M0 ed M1 i rispettivi centri di curvatura, e immaginiamo un filo flessibile e inestensibile che, fissato a un suo capo in M1, aderisca perfettamente all’arco di evoluta M1M0 e se ne distacchi poi seguendo la tangente a Γ in M0, fino a P0. Se si svolge il filo aderente alla e. tenendolo sempre teso e in modo che la parte rettilinea si mantenga sempre tangente alla e. stessa, il suo estremo libero descriverà l’evolvente C. La costruzione indicata, oltre a rendere ragione dei nomi di e. ed evolvente, mostra che esistono infinite curve evolventi di una data curva.