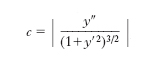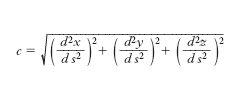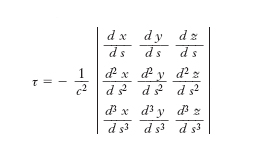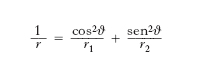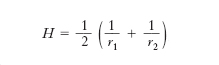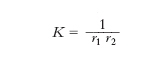curvatura
Lo stato generico di un ente geometrico o fisico di scostarsi da un andamento rettilineo o piano.
C. di una curva piana
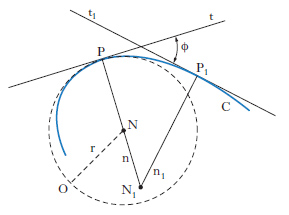
Elemento definito punto per punto della curva, che misura la rapidità con la quale la curva si discosta dalla tangente, la rapidità cioè con la quale essa si discosta dall’andamento rettilineo. Precisamente, dati una curva piana C e un arco PP1 di essa, si traccino le tangenti t, t1 a C nei punti P e P1. L’angolo ϕ formato da t e t1 (fig. 1) risulta tanto più grande quanto più l’arco PP1 si discosta da un segmento rettilineo (almeno se P1 è prossimo a P). Si chiamano: a) c. media dell’arco PP1, il rapporto tra l’angolo ϕ e la lunghezza dell’arco stesso; b) c. nel punto P della linea C, il limite c di detto rapporto al tendere di P1 a P. Per un cerchio di raggio r la curva è la stessa in tutti i punti, ed è uguale a 1/r. Segue da ciò che, essendo c la c. di una linea C in un punto P, esiste un cerchio O ben determinato (di raggio r = 1/c) tangente alla curva in P e avente in P la stessa c. della C. È questo il cerchio osculatore alla C in P. Il suo raggio r = 1/c (cioè l’inverso della c.) si chiama il raggio di c. della C in P; il suo centro N si chiama il centro di c. della C in P (esso è la posizione limite del punto N1 in cui si incontrano le normali n e n1 alla C, rispettivamente in P e P1). La c. ha l’espressione:
,
se y = y(x) è l’equazione cartesiana ortogonale della C, e y′, y″, le derivate prima e seconda della funzione y(x) calcolate nel punto P.
C. di una curva sghemba
La prima c. (o flessione), che misura ancora la rapidità dello scostamento dall’andamento rettilineo della curva C in un suo punto P, si definisce in modo identico a quanto si è fatto per una curva piana come limite al quale tende il rapporto tra l’angolo formato dalle tangenti a C in due punti P e P1 e la lunghezza dell’arco PP1, quando P1 tenda a P. La prima c. di una linea sghemba C si può esprimere nella forma:
mediante le derivate seconde delle funzioni x(s), y(s), z(s) che forniscono una rappresentazione parametrica della linea C in funzione dell’ascissa curvilinea s.
La seconda c. (o torsione), misura invece la rapidità con la quale la C si discosta dall’andamento piano (quanto più grande è la torsione, tanto più rapidamente la curva si scosta, allontanandosi da P, dal suo piano osculatore in P). Essa si definisce in modo analogo alla prima c., cioè come limite cui tende il rapporto tra l’angolo formato dai piani osculatori alla C nel punto P e in un punto P1 prossimo a P (o anche l’angolo formato dalle binormali in P e P1) e la lunghezza dell’arco PP1, al tendere di P1 a P. La torsione si indica generalmente con τ, e la sua espressione è:
,
dove c è la prima c. e nel determinante compaiono le derivate, prime, seconde e terze, delle tre funzioni x(s), y(s), z(s) che rappresentano parametricamente la curva mediante l’ascissa curvilinea s. Se una curva ha la prima c. nulla in tutti i suoi punti, essa è necessariamente una retta; se invece è nulla in tutti i punti la seconda c., si tratta necessariamente di una curva piana (il viceversa, in entrambi i casi, è ovvio).
C. di una superficie
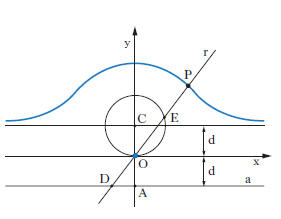
La considerazione della rapidità e del modo in cui una superficie si discosta dal piano tangente a essa in un suo punto P dà luogo a considerazioni più delicate. Ci limiteremo a riassumere alcuni risultati fondamentali. Si dimostra (teorema di Meusnier) che è sufficiente limitarsi alla considerazione delle sezioni normali, cioè delle linee piane che si ottengono tagliando la superficie, S, con i piani per la normale n a S in P: il raggio di c. ρ di una qualunque curva C tracciata su S per un punto P è infatti pari al prodotto del raggio di c. r della sezione normale c avente in P la stessa tangente della curva data, per il coseno dell’angolo Θ che risulta formato dai piani osculatori alle due curve, cioè: ρ = r cos Θ. Al raggio di c., r, di una sezione normale si dà il segno + oppure − a seconda che essa volga la concavità o la convessità dalla parte del verso positivo della normale (supposta orientata). Tale raggio r ammette un massimo r1 e un minimo r2 in corrispondenza a due sezioni normali c1, c2 tra di loro perpendicolari ( sezioni normali principali). La c., 1/r, di una qualsiasi altra sezione normale C si esprime allora mediante la formula di Eulero:
,
ϑ essendo l’angolo formato dalla sezione normale con la prima delle sezioni normali principali. Per quel che riguarda l’andamento della superficie S, nelle vicinanze di P, si sogliono allora considerare: a) la c. media,
b) la c. totale di S in P,
(introdotta da K.F. Gauss nel 1827). Se K è positiva (cioè r1 e r2 hanno lo stesso segno) ciò vuol dire che le sezioni normali volgono tutte la concavità dalla stessa parte (rispetto alla normale orientata): la superficie S in P ha, all’incirca, la forma di una scodella, il punto P si dice ellittico (come il punto E, fig. 2). Se K è negativa (r1 e r2 hanno segni opposti) risulta invece che le sezioni normali principali volgono la concavità secondo versi opposti: S ha in P, all’incirca, la forma di una sella, il punto P si dice iperbolico (come il punto F, fig. 2). Se infine K è nulla il punto P si dice parabolico: la superficie ha quindi una forma che, di solito, ricorda quella di un cilindro o di un cono in prossimità di un punto distinto dal vertice (come il punto G, fig. 2). La grande importanza della c. totale risiede nel fatto che essa è invariante per flessioni (o per applicabilità).
Come secondo Gauss si può introdurre la c. intrinseca di una superficie, così si può parlare della c. dello spazio (➔) tridimensionale, esprimibile mediante le formule dell’analisi. Il concetto si è rivelato di fondamentale importanza in fisica, nella teoria della relatività generale (➔ relatività).