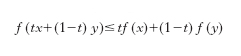convessità
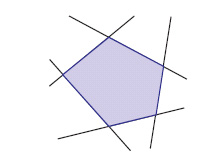
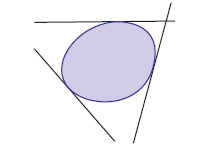
convessità Una figura (piana o solida) è detta convessa se, dati due suoi punti qualunque, il segmento che li congiunge appartiene interamente alla figura. Più in generale questa definizione si applica a tutti i sottoinsiemi di un generico spazio vettoriale reale. Casi notevoli: a) un angolo è convesso se ha ampiezza minore di 180°, nel qual caso i prolungamenti dei lati sono esterni all’angolo; b) un poligono è convesso (fig. 1) se tali sono tutti i suoi angoli, ossia se esso giace tutto da una banda rispetto alla retta di ciascun suo lato; c) la regione piana delimitata da una curva chiusa (o da un arco aperto e dalla corda che ne congiunge gli estremi) è convessa se essa giace tutta da una banda rispetto alla tangente in un qualsiasi punto del contorno (fig. 2); d) un poliedro è convesso se esso giace tutto in uno stesso semispazio rispetto a ciascuna delle sue facce. La teoria delle figure piane convesse, dei solidi convessi e dei loro contorni (contorni detti rispettivamente nei due casi ovali e ovaloidi) è un ramo, in pieno sviluppo, della matematica (a partire dagli studi di H. Minkowski, C. Carathéodory, D. Hilbert ecc.). Funzioni convesse Una funzione f è convessa in un dominio convesso C (per es., un intervallo) se per ogni x, y in C si ha
con 0 〈 t 〈 1; se nell’espressione precedente non vale mai il segno di uguaglianza, la funzione f è detta strettamente convessa. Una funzione f è detta invece concava se −f è convessa.