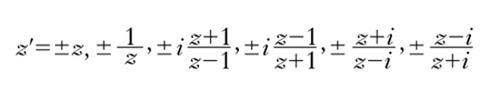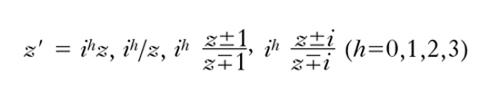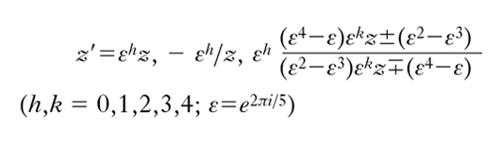poliedro

Solido geometrico limitato da un numero finito di poligoni disposti in modo tale che ciascun lato sia comune a due e a due soli poligoni (come, per es., nel cubo, nelle piramidi, nei prismi): facce del p. sono i poligoni che lo limitano; spigoli, vertici del p. rispettivamente i lati e i vertici degli stessi poligoni; diedri del p. gli angoli diedri formati da 2 facce aventi un lato in comune; angoloidi del p. gli angoloidi formati da tutte le facce concorrenti in un vertice.

La nozione di p. nel suo significato originario e più semplice indica la parte di spazio racchiusa da una superficie, detta superficie poliedrica, costituita da poligoni in numero non inferiore a 4. Talvolta, però, è proprio a tale superficie che si dà il nome di p.: in questo caso non è più essenziale considerare la regione limitata da essa, che anzi può addirittura mancare, come avviene, per es., se la superficie è aperta.

fig. 1

fig. 2

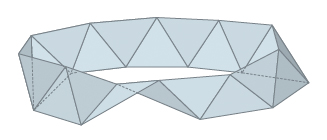
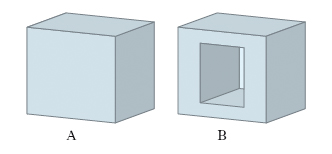
Un p. è convesso se il piano di appartenenza di ciascuna faccia lascia tutto il p. in uno solo dei 2 semispazi individuati dal piano; altrimenti il p. si dice concavo. Per i p. sono possibili classificazioni di vario tipo: topologica, proiettiva, affine, metrica, e così via. La classificazione metrica porta a distinguere i p. in regolari, semiregolari ecc. I prismi si distinguono da un punto di vista affine dagli altri tipi di p., così come le piramidi da un punto di vista proiettivo; è anche di natura proiettiva la classificazione in base al numero delle facce e al numero dei lati di esse. I p. di 4, 5, 6, … 12, …, 20 facce si dicono rispettivamente tetraedro, pentaedro, esaedro, …, dodecaedro, …, icosaedro. Infine, la classificazione topologica distingue i p. unilateri da quelli bilateri, a seconda che la superficie del p. presenti una sola faccia o pagina (come è, per es., un p. che triangoli un nastro di Möbius: fig. 1) o 2 facce (fig. 2), e suddivide questi ultimi a seconda del genere (➔).

P. archimedei

fig. 3

Particolare tipo di p. semiregolari che hanno per facce poligoni regolari (non necessariamente uguali fra loro) e in cui tutti gli angoloidi sono uguali fra loro; ciascuno dei p. archimedei ammette una sfera circoscritta e quindi un centro, ed è mutato in sé da un opportuno gruppo di rotazioni. Ne esistono 15 tipi (fig. 3): cubo simo (che ha per facce 32 triangoli e 6 quadrati), dodecaedro simo (80 triangoli, 12 pentagoni), cubottaedro (8 triangoli, 6 quadrati), icosidodecaedro (20 triangoli, 12 pentagoni), antiprisma archimedeo o prisma storto (2 poligoni regolari uguali – non triangoli – aventi un numero qualunque di lati, triangoli equilateri in numero doppio del numero dei lati dei poligoni), rombicubottaedro (8 triangoli, 18 quadrati), prisma archimedeo (2 poligoni regolari uguali, non quadrati, e tanti quadrati quanti sono i lati dei poligoni), tetraedro tronco (4 triangoli, 4 esagoni), ottaedro tronco (6 quadrati, 8 esagoni), icosaedro tronco (12 pentagoni, 20 esagoni), cubo tronco (8 triangoli, 6 ottagoni), dodecaedro tronco (20 triangoli, 12 decagoni), rombicosidodecaedro (20 triangoli, 30 quadrati, 12 pentagoni), cubottaedro tronco (12 quadrati, 8 esagoni, 6 ottagoni), icosidodecaedro tronco (30 quadrati, 20 esagoni, 12 decagoni).

P. duali

Sono 2 p. tali che a ogni faccia dell’uno si possa far corrispondere un angoloide dell’altro, in modo che ai lati e ai vertici della faccia corrispondano gli spigoli e gli angoli dell’angoloide. Per es., il cubo e l’ottaedro sono p. duali, così come il dodecaedro e l’icosaedro; il tetraedro è invece duale di sé stesso. Due p. duali si possono ottenere l’uno dall’altro mediante una polarità, per es. rispetto a una sfera; usualmente, se il p. ha un centro, la sfera si prende concentrica con il poliedro.

P. intrecciati

Tipo di p. nei quali due facce possono avere punti di intersezione anche al di fuori di un eventuale spigolo comune. Particolari p. intrecciati sono i p. stellati.

P. regolari

fig. 4A

tabella

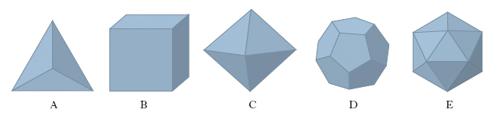
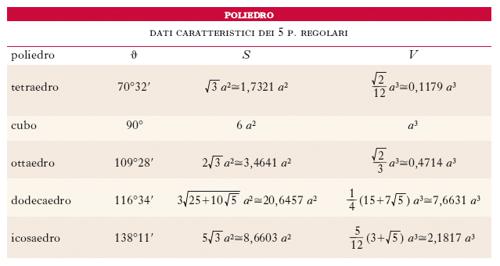
Detti anche p. o solidi platonici, perché citati nel Timeo di Platone, sono p. convessi che hanno per facce p. regolari uguali e in cui tutti gli angoloidi sono uguali fra loro (come pure gli angoli diedri). Esistono solo 5 tipi di p. regolari: tetraedro (ha per facce 4 triangoli equilateri: fig. 4A), esaedro o cubo (ha per facce 6 quadrati: fig. 4B), ottaedro (ha per facce 8 triangoli equilateri: fig. 4C), dodecaedro (ha per facce 12 pentagoni regolari: fig. 4D), icosaedro (ha per facce 20 triangoli equilateri: fig. 4E). Per essi esiste sempre una sfera inscritta (ossia tangente alle facce), una circoscritta (cioè passante per i vertici) e una terza tangente agli spigoli. Esse hanno lo stesso centro, che è il centro di simmetria del poliedro. La tabella fornisce, per ognuno dei 5 p. regolari, l’angolo ϑ (a meno di 1′) formato da due facce contigue e inoltre la superficie S e il volume V in funzione dello spigolo a del p.; sorprendente è il fatto che il volume dell’ottaedro è 4 volte quello del tetraedro.

Nello spazio euclideo a n dimensioni (n≥5) esistono 3 soli tipi di p. (o meglio di politopi) regolari, che si richiamano rispettivamente al tetraedro, al cubo e all’ottaedro regolare dello spazio ordinario. Per n = 4, a questi 3 tipi se ne aggiungono altri 3. Gruppi dei p. regolari Sono gruppi finiti di rotazioni attorno a un punto fisso O dello spazio che trasformano in sé un p. regolare o una piramide regolare o una doppia piramide regolare. Essi sono gli unici gruppi finiti di rotazioni attorno a O e sono isomorfi ai gruppi finiti di sostituzioni lineari non degeneri sopra una variabile complessa z′ = (αz+β)/(γz+δ) (con z, z′ variabili complesse, α, β, γ, δ costanti complesse e αδ−βγ≠0) ovvero ai gruppi finiti di proiettività sopra una retta. Ne esistono di 5 tipi: a) gruppi ciclici o della piramide regolare: z′ = ε^hz (h = 0, 1, …, n−1; ε = e^2πi/n); b) gruppi diedrali D_n o della doppia piramide: z′ = ε^hz, ε^h/z (h = 0, 1, …, n−1; ε = e^2πi/n); c) gruppo T₁₂ del tetraedro:

d) gruppo O₂₄ del cubo o dell’ottaedro:

e) gruppo I₆₀ dell’icosaedro o del dodecaedro:

P. semiregolari

Sono particolari p. convessi che hanno alcuni dei caratteri propri dei p. regolari. Si hanno 2 tipi di p. semiregolari. Il primo è quello dei p. archimedei , il secondo tipo è quello dei p. che hanno facce tutte uguali ma non regolari e angoloidi non tutti uguali ma regolari.

P. stellati

fig. 5

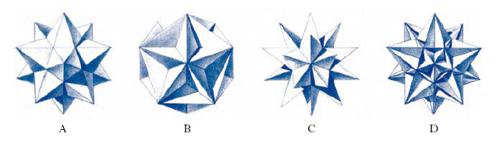
Particolari p. non convessi e intrecciati che si ottengono a partire da un p. convesso ampliando le sue facce fino a incontrare altre opportune facce del p. medesimo. Notevoli i p. regolari stellati o p. di Poinsot; ne esistono 4 tipi e tutti hanno sia le facce sia gli angoloidi uguali e regolari (fig. 5): il dodecaedro stellato a facce ordinarie che ha specie 3, ossia una qualsiasi semiretta uscente dal centro del p. incontra 3 facce del p., il dodecaedro a facce stellate e a 12 vertici, che ha anch’esso specie 3, il dodecaedro a facce stellate e a 20 vertici e l’icosaedro stellato, che hanno invece specie 7.