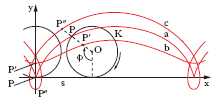
cicloide
Curva descritta da un punto rigidamente collegato a un cerchio K (epiciclo), che rotoli nel piano, senza strisciare, su una retta fissa s. Una c. (v. fig.) si dice: a) ordinaria, se il punto P giace sulla circonferenza di K; b) accorciata, se il punto P′, è interno a K; c) allungata, se il punto P″ è esterno a K. A ogni giro completo del cerchio rotolante corrisponde un ‘arco completo’ di c.: la c. risulta una curva trascendente, costituita da infiniti archi uguali tra di loro. Le coordinate cartesiane x, y di un punto della c. si possono esprimere mediante le equazioni parametriche x=r ϕ−h sen ϕ, y=r−h cos ϕ in cui r è il raggio del cerchio generatore, h la distanza del punto generatore dal centro del cerchio; il parametro ϕ è l’angolo di cui, in una generica posizione, risulta ruotato in verso orario il raggio che inizialmente andava al punto di contatto. Si hanno i tre tipi di cicloide sopra nominati a seconda che sia h=r, h〈r, h>r.
Le misure relative alla c. ordinaria (r = raggio del cerchio generatore) sono: lunghezza di un arco completo = 8 r (teorema di Wren); area della superficie compresa tra un arco completo e la retta fissa = 3 π r2 (triplo dell’area del cerchio). Quest’ultimo risultato (Roberval) era stato intuito da Galileo in base alla pesatura di lamine aventi la forma delle due superfici.
Le proprietà notevoli della c. ordinaria sono:
a) è la curva di «minimo tempo» (brachistocrona): cioè, dati due punti A, B in un piano verticale, un grave che scenda, in assenza di attrito, da A a B lungo un arco di curva impiega il minimo tempo se l’arco di curva è un arco di c.;
b) è la curva «dello stesso tempo» (tautocrona): cioè, preso un arco completo di c. in un piano verticale, con la concavità verso l’alto, un punto pesante P che cada lungo di esso senza attrito impiega sempre lo stesso tempo a giungere al punto più basso dell’arco, qualunque sia la posizione da cui il punto sulla curva è abbandonato a sé stesso, a partire dalla quiete.