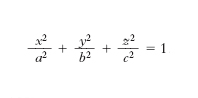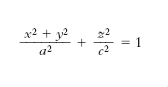ellissoide
In geometria, ogni superficie del 2° ordine, la cui equazione può essere ridotta alla forma
,
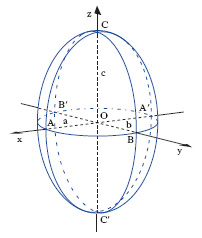
nella quale le tre costanti a, b, c ( semiassi dell’e.) sono in generale disuguali. A tale forma può essere ridotta l’equazione di ogni quadrica: a) dotata di punti reali; b) a punti ellittici, cioè tale che il piano tangente in un punto reale P ha in comune con la superficie, dal punto di vista reale, solo il punto P; c) limitata. Il volume della regione di spazio racchiusa dall’e. di semiassi a, b, c è espresso da (4π/3)abc. L’e. possiede un centro di simmetria O (è una quadrica a centro), tre piani di simmetria a due a due ortogonali ( piani principali), le cui intersezioni sono i tre assi di simmetria dell’e. ( assi principali, rappresentati in fig. dagli assi coordinati x, y, z). Le tre coppie di punti AA′, BB′, CC′ che si ottengono intersecando l’e. con i suoi assi principali si chiamano vertici. In particolare, l’ e. di rotazione (o di rivoluzione, o rotondo) si ottiene facendo descrivere a un’ellisse una rotazione intorno a uno dei suoi assi: l’equazione di un e. di rotazione si scrive perciò nella forma
(supponendo di far ruotare attorno all’asse z una ellisse del piano x z, riferita ai suoi assi).
L’e. si dice allungato (o schiacciato) secondo che la rotazione dell’ellisse avvenga intorno all’asse maggiore o all’asse minore dell’ellisse (nel primo caso è c>a; nel secondo, è c〈a).