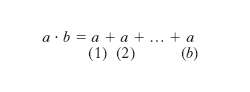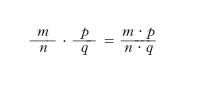moltiplicazione

Biologia

L’accrescimento numerico degli organismi viventi mediante la riproduzione biologica. Il coefficiente di m. è diverso nelle diverse specie. L’aumento degli individui di una specie, nelle successive generazioni, è contrastato da vari fattori: cibo, predatori, parassiti, eventi climatici e meteorologici, azione diretta o indiretta dell’uomo ecc.. La lotta per l’esistenza dovuta alla m. è una delle cause dell’evoluzione, perché determina la selezione naturale. Le specie animali e vegetali che si moltiplicano con ritmo insufficiente a bilanciare le perdite, sono destinate a estinguersi, com’è infatti avvenuto, anche in epoca storica, per molte di esse.

In botanica, la m. è un modo di riproduzione molto diffuso. Nei funghi e in molte alghe, ha luogo mediante conidi, spore, frammenti ecc., sia nella fase aploide sia in quella diploide del ciclo biologico. Quando si verificano condizioni avverse subentra la riproduzione sessuata. Nelle piante superiori la m. avviene mediante talea, propaggine, margotta, divisione, innesti, metodi sfruttati in agraria per le piante coltivate. La m. avviene anche attraverso la formazione di organi di conservazione (bulbi, bulbilli, cormi ecc.). Con la m. si formano individui geneticamente identici.

Matematica

Una delle quattro operazioni razionali (le altre sono l’addizione, la sottrazione e la divisione), così chiamate perché, se si eseguono su numeri razionali, il risultato è ancora un numero di questo tipo. Il simbolo della m. è il segno × o anche un punto posto tra i numeri da moltiplicare (detti fattori). Si può però omettere ogni simbolo di operazione scrivendo l’uno accanto all’altro i due numeri sui quali la m. opera. Si scriverà perciò: 1) a×b; 2) a∙b; 3) ab (leggi: a per b). Il simbolo × fu introdotto da W. Oughtred. Moltiplicare a per b, se si tratta di numeri interi, significa addizionare b termini tutti uguali ad a:

La m. di due frazioni si riconduce alla m. dei numeri interi in quanto si ha:

L’operazione di m. si estende poi ai campi dei numeri reali e dei numeri complessi, che sono ampliamenti del campo dei numeri razionali. In ogni caso la m. di due numeri reali concordi dà un risultato positivo, di due numeri discordi un risultato negativo. È questa la cosiddetta regola dei segni.

La m. gode delle seguenti proprietà: 1) proprietà associativa: a∙(b∙c)=(a∙b)∙c; 2) proprietà distributiva: a ∙ (b+c)=a∙b+a∙c; 3) proprietà commutativa: a∙b=b∙a; 4) legge di annullamento del prodotto: un prodotto è uguale a zero, quando e soltanto quando almeno uno dei fattori è uguale a zero; 5) esistenza di un elemento neutro (unità moltiplicativa = 1): 1∙a=a∙1=a; 6) esistenza e unicità dell’inverso: dato un numero a≠0, esiste uno e un solo numero a′=1/a=a^–1 tale che a∙ a′=1; 7) invertibilità dell’operazione: dati due numeri a≠0, b, esiste sempre uno e un solo numero x tale che a∙x=b. Le proprietà ora indicate valgono tutte sia nel campo dei numeri razionali, sia in quelli dei numeri reali o complessi. Se si considera invece la m. tra numeri interi, restano valide solo le prime cinque di esse, mentre nella m. tra quaternioni perde validità la proprietà commutativa ma restano le altre. Infine, nella m. tra matrici quadrate di uno stesso ordine, valgono le sole proprietà 1, 2, 5.

Con significato più ampio e generale, il termine m. si usa a proposito di ogni legge binaria di composizione in un insieme, qualora siano soddisfatte tutte o solo alcune delle proprietà della m. ordinaria. Si parla perciò di m. in un campo, in un corpo, in un anello, in un gruppo, in un gruppoide.

Formule di m. In trigonometria, formule che danno le funzioni trigonometriche di un multiplo di un angolo in funzione di quelle dell’angolo.

Fisica

In fisica nucleare, fattore di m. in una reazione di fissione, è il rapporto tra il numero di neutroni prodotti e il numero di neutroni assorbiti e dispersi; perché una reazione di fissione si autosostenga occorre che il fattore di m. sia non minore dell’unità.