prospettiva
Rappresentazione degli oggetti nello spazio (nel disegno, nella pittura ma anche nella scultura in bassorilievo o altorilievo), in modo da raggiungere l’effetto della terza dimensione su una superficie bidimensionale.
Arte
Nella storia delle arti figurative il termine p. viene usato in modo generico per indicare i diversi modi di rappresentazione dello spazio. Per tutta l’antichità e il Medioevo non esiste distinzione tra ottica e p.: sono gli artisti fiorentini del 15° sec. a usare il termine (dal latino perspectiva) per indicare il modo di rappresentare gli oggetti secondo i principi scientifici dell’ottica.
Antichità
I popoli del Vicino Oriente antico non conoscono lo scorcio e per questo motivo i loro cicli pittorici sono senza p.: alla disposizione in profondità degli oggetti e delle persone si allude mediante lo scaglionamento (verticale o orizzontale) delle singole immagini, l’una di seguito all’altra.
In Grecia, invece, il problema prospettico trova un’intensa elaborazione teorica, matematica e artistica. Plinio attribuisce l’invenzione delle imagines obliquae (cioè dello scorcio) a Kimon di Kleonai, un pittore vascolare della fine del 6° sec. a.C.; ma è con Polignoto, come si deduce dalle fonti letterarie, che si hanno i primi tentativi di pittura illusionistica in grandi scene dipinte. La padronanza dello scorcio porta all’impostazione di problemi prospettici: Agatarco di Samo sperimenta la p. nel dipingere le scene teatrali per le tragedie di Eschilo, e scrive un commentario di cui si serviranno Anassagora e Democrito per le loro teorie. Insieme alle ricerche prospettiche si elaborano quelle chiaroscurali, studiando le ombreggiature, per dare risalto e profondità alle immagini: problemi risolti nell’ultimo trentennio del 5° sec. a.C. da Apollodoro di Atene, detto skiagràphos («pittore di ombre»).
Per quanto riguarda la pittura murale di carattere scenografico, nota solo da derivazioni di età romana, si possono indicare i cicli pompeiani della casa del Labirinto e della villa dei Misteri, appartenenti alla fase più precoce del secondo stile. Di età augustea è la decorazione della stanza delle Maschere (Roma, Palatino), dove una équipe di modesti decoratori, che ripete motivi di repertorio, realizza elaborate scansioni spaziali e perfette fughe prospettiche che presuppongono un pieno possesso dei fondamenti teorici della prospettiva. L’ulteriore sviluppo della pittura parietale prevede il progressivo abbandono della p. rigorosa per far posto alle sofisticate e capricciose soluzioni del terzo e quarto stile.
Dal Medioevo al 20° secolo
Nell’arte bizantina, caratterizzata da un senso di spazio indefinito, gli oggetti sono rappresentati ortogonalmente, in p. inversa. Elementi paesaggistici o architettonici sono raramente presenti o, quando vi sono (mosaici veneti e siciliani del 12° sec.), assumono una funzione di semplice accompagnamento ritmico. Tale situazione cambia, nel mondo occidentale, lungo il corso del 13° sec., in concomitanza di un rinnovato interesse per il senso corporeo degli oggetti (P. Cavallini, 1291 ca., mosaici di S. Maria in Trastevere, Roma), e pone le premesse per il primo tentativo di rivalutazione della p. che ha luogo con Giotto: ad Assisi e, quindi, nella cappella degli Scrovegni a Padova è data una plausibilità spaziale alla rappresentazione, pur non giungendo ancora alla definizione di un’unità spaziale.
La definitiva riscoperta della p. centrale avviene a Firenze, all’inizio del 15° sec., a opera di F. Brunelleschi, autore di due tavolette dimostrative rappresentanti Il battistero di Firenze e Palazzo Vecchio (perdute), realizzate seguendo precise regole geometriche, tenendo conto del punto di fuga centrale e della distanza dell’osservatore dalla superficie dipinta. La prima trattazione sistematica nota del metodo di riduzione prospettica secondo il principio proiettivo, ossia del taglio della piramide, è quella di L.B. Alberti (Della pittura, 1436); ma la p. era allora già ben nota agli artisti fiorentini, da Donatello a Masaccio, a Paolo Uccello (con un senso più astrattamente scientifico), fino a Piero della Francesca (autore anche di un trattato, De prospectiva pingendi, 1480), momento paradigmatico della p. quattrocentesca: la realtà si ricostruisce architettonicamente, riferendo ciascun solido al modello ideale dei corpi regolari.
Molto diverso è invece l’uso che della p. fa A. Mantegna, utilizzando la p., nei diversi tipi di visione, con un fine dichiaratamente illusionistico. Nell’opera di Raffaello e della sua scuola si accentuano le applicazioni della p. architettonica dipinta che, affermatesi nel corso del 16° sec., raggiungeranno le più alte applicazioni pratiche e teoriche nel 17° e 18° sec. (➔ quadraturismo). Attraverso Correggio, che sviluppa lo sfondato illusionistico delle volte affrescate, deriva la grande decorazione barocca che, grazie al sapiente uso della p. illusionistica e, a volte, della quadratura, otterrà effetti fantasiosamente scenografici (G. Lanfranco, Pietro da Cortona, G.B. Gaulli, A. Pozzo).
Ancora nel 19° sec. l’insegnamento della p. è il cardine dell’educazione accademica, ma con l’affermarsi dell’impressionismo si giunge a un progressivo abbandono della costruzione geometrica: prime consapevoli deroghe dell’obiettività prospettica si hanno con P. Cézanne, dove i piani orizzontali si ribaltano verso l’osservatore. Con il cubismo il rifiuto della p. assume una connotazione dichiaratamente polemica. Gli ulteriori sviluppi delle arti figurative sono stati fortemente influenzati dalla rivoluzione cubista, capovolgimento radicale della visione prospettica rinascimentale.
Per p. aerea si intende l’uso degli effetti atmosferici, di sfocatura e di inazzurramento, come mezzi per restituire l’effetto di distanza, sviluppato dalle ricerche di Leonardo e utilizzato in tutte le epoche successive.
Matematica
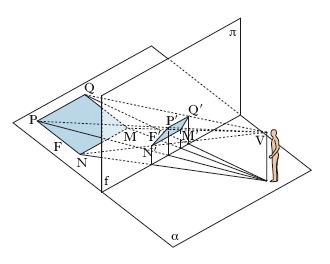
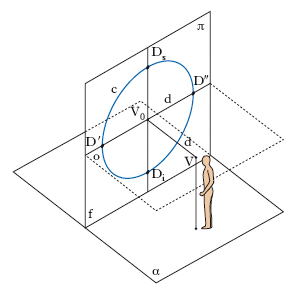
Parte della geometria descrittiva che si propone di elaborare le regole grafiche per costruire di un qualunque oggetto reale un’immagine bidimensionale analoga a quella data dalla visione diretta. La p. lineare costruisce le immagini, quali risulterebbero osservando gli oggetti da un unico centro di vista (o centro di p.) V. Si consideri il quadro π come una superficie piana trasparente interposta tra la figura da rappresentare e il centro di vista V (cioè l’‘occhio’). I raggi visuali uscenti da V e diretti ai punti M, N, P, Q della figura obiettiva F (fig. 1) attraversano il piano π rispettivamente nei punti M′, N′, P′, Q′. La figura M′ N′ P′ Q′ costituisce l’immagine (la p.) F′ sul quadro π della figura obiettiva MNPQ. La p. non è altro perciò che una proiezione centrale dal centro V sul quadro π; a seconda che V si supponga al finito o all’infinito, si avranno rispettivamente la p. centrale (o conica) o la p. parallela (o rapida, o assonometrica). È da notare che, data la figura obiettiva, la sua p. è univocamente determinata, ma non altrettanto può dirsi per il problema inverso, che risulta determinato solo se, oltre alla p. F′della figura F, si conoscono altri elementi. In generale, l’oggetto o gli oggetti da rappresentare si suppongono appoggiati su di un piano orizzontale α detto piano stazione o geometrale, mentre π si suppone verticale (in questo caso la p. si dice p. normale; se il quadro π non è verticale si ha la p. con quadro inclinato). Si chiama fondamentale (o linea di terra) la retta f (fig. 2) intersezione del geometrale con il quadro, orizzonte la retta o intersezione del quadro con il piano orizzontale passante per il centro di vista V. La semiretta per V perpendicolare al quadro si dice raggio visuale principale o retta principale e il suo punto d’intersezione V0 con il quadro si dice punto principale della prospettiva. Si chiama distanza principale la distanza d tra V e V0, circonferenza di distanza la circonferenza c di centro V0 e raggio d giacente su π; i punti esterni a c, i punti di c, i punti interni a c sono punti di fuga delle rette che formano con il quadro, rispettivamente, un angolo minore, uguale, maggiore di 45°. Punti principali di distanza, rispettivamente sinistro D′ e destro D″, inferiore Di e superiore Ds, sono detti i punti d’intersezione della circonferenza di distanza rispettivamente con l’orizzonte e con la perpendicolare all’orizzonte per V0; D′ e D″ sono punti di fuga delle rette del geometrale formanti con la fondamentale un angolo di 45°, mentre V0 è il punto di fuga delle rette del geometrale perpendicolari al quadro e Di, Ds sono punti di fuga delle rette perpendicolari all’orizzonte e formanti un angolo di 45° con il geometrale. Queste osservazioni, insieme con le precedenti figure, chiariscono le fig. 3 e 4, nelle quali è costruita la p. di un quadrato MNPQ del geometrale (fig. 3A) e la p. di un quadrato giacente su un piano di profilo, perpendicolare cioè alla fondamentale (fig. 3B); nelle fig. è dato il ribaltamento M*N*P*Q* sul quadro del quadrato MNPQ. Nella fig. 4 si è ottenuta la p. di una serie di segmenti AB, BC, CD uguali e consecutivi appartenenti a una retta r del geometrale. Si è utilizzato a tale scopo il ribaltamento di r sulla fondamentale e il punto di misura destro M″r della retta r, che è il punto di fuga delle rette AA*, BB*, CC*, DD*.
L’esposizione teorica della p. come parte della geometria, e non più dell’ottica, entro la quale si era sviluppata, si può far risalire a F. Commandino (1558) e al suo discepolo Guidobaldo Dal Monte (1600). Essa, che troverà la sua sistemazione definitiva come capitolo della geometria descrittiva al principio del 19° sec. (G. Monge), rappresenta storicamente il punto di partenza della geometria proiettiva.