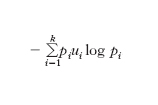informazione

Notizia, dato o elemento che consente di avere conoscenza più o meno esatta di fatti, situazioni, modi di essere. In senso più generale, anche la trasmissione dei dati e l’insieme delle strutture che la consentono.

L’espressione tecnologia delle i. è la traduzione italiana di information technology, utilizzata comunemente per indicare l’insieme di tutte le tecnologie relative allo hardware dei computer, al software, alla creazione di reti e in genere a tutto ciò che riguarda il digitale. È in genere indicata con l’acronimo ICT (information and communications technology), che rivela lo stretto legame esistente fra tecnologia delle i. e trasferimento dei dati.

Biologia

I. genetica L’insieme dei messaggi ereditari che danno luogo alla manifestazione dei vari caratteri dell’organismo. La prima approssimazione alla conoscenza del modo in cui l’i. genetica è registrata nella cellula venne come conseguenza della scoperta delle leggi di Mendel (1900), con la dimostrazione che sono i geni, nel corso dello sviluppo individuale, a determinare la manifestazione di tutti i caratteri. Nel decennio 1910-20, T.H. Morgan e i suoi collaboratori dimostrarono che i geni sono localizzati in un ordine rigorosamente definito e costante nei cromosomi che si trovano nel nucleo della cellula. La scoperta della trasformazione nei batteri (O. Avery e C. McLeod, 1944) e le ricerche di A.D. Hershey e M. Chase (1952) sui batteriofagi dimostrarono che la sostanza che reca e trasmette l’i. genetica è il DNA. L’avvento della biologia molecolare ha reso possibile la conoscenza della struttura degli acidi nucleici, la decifrazione del codice genetico e la scoperta del meccanismo per cui l’i. registrata nel nucleo della molecola filamentosa di DNA viene trasmessa, per mezzo dell’RNA, ai ribosomi situati nel citoplasma, dove vengono costruite le molecole proteiche.

Diritto

Diritto all’informazione

Il diritto all’i. – alcuni studiosi preferiscono utilizzare la locuzione libertà di i. – rileva sotto due o tre diversi aspetti: come libertà di informare e come diritto ad essere informati, oppure (secondo Lavagna) come diritto di informare, cioè di trasmettere notizie agli altri, come diritto di informarsi, cioè di attingere i. da più fonti, e come diritto di essere informati. Mentre è pacifico che il primo aspetto rientri nella più generale libertà di manifestazione del pensiero di cui all’art. 21 Cost., più problematico appare il legame con il testo costituzionale nel caso del secondo e del terzo aspetto. A differenza di altri testi costituzionali (art. 5 Legge fondamentale Germania 1949; art. 20-D Cost. Spagna 1978) e di quanto previsto da dichiarazioni internazionali e/o sovranazionali dei diritti (art. 19 Dichiarazione universale dei diritti dell’uomo 1948; art. 10 CEDU; art. 19 Patto internazionale sui diritti civili e politici 1966; art. 11 Carta dei diritti fondamentali dell’U.E.), la Costituzione italiana non prevede espressamente un diritto all’informazione.

Molti studiosi – è il caso, ad esempio, di C. Mortati – hanno ricondotto il diritto di essere informati (sia come diritto di ricevere i. che come diritto di ricercarle) all’art. 21 Cost., sulla base anche di una costante giurisprudenza costituzionale, che ha considerato questo diritto un «risvolto passivo della libertà di manifestazione del pensiero». D’altra parte, proprio in virtù del collegamento con l’art. 21 Cost. e facendo proprie le tesi espresse dalla stessa Corte costituzionale, alcuni autori (ad esempio, Paladin) hanno parlato di un mero interesse all’i. e non di un vero e proprio diritto azionabile in sede giudiziaria. Altri studiosi – è il caso, invece, di C. Esposito – hanno negato l’automatico collegamento tra diritto all’i. e libertà di manifestazione del pensiero. Alcuni autori, infine, hanno configurato il diritto all’i. come una conseguenza del principio democratico, poiché un regime democratico (Democrazia) necessita sempre di una pubblica opinione vigile e informata (Comunicazione politica): questa esigenza generale di pubblicità, che si specificherebbe ulteriormente nel principio dell’accesso ai documenti delle pubbliche amministrazioni (l. n. 349/1986; l. n. 142/1990; d.lgs. 267/2000; l. n. 15/2005), trova un limite nella tutela del segreto.

Tra le varie forme di segreto, il più importante è sicuramente il c.d. segreto di Stato, recentemente ridisciplinato con la l. n. 124/2007, che ha sostituito la precedente l. n. 801/1977. L’apposizione del segreto di Stato deve avere una giustificazione costituzionale, nel senso che deve essere fondata sulla tutela di interessi costituzionalmente protetti (la l. n. 124/2007 si riferisce appunto alla diffusione di qualunque cosa che possa recare «danno all’integrità della Repubblica, anche in relazione ad accordi internazionali, alla difesa delle istituzioni poste dalla Costituzione a suo fondamento, all’indipendenza dello Stato rispetto agli altri Stati e alle relazioni con essi, alla preparazione e alla difesa militare dello Stato»). In ogni caso, l’apposizione del segreto di Stato non può riguardare «fatti di terrorismo o eversivi dell’ordine costituzionale» (l. n. 124/2007), laddove la l. n. 801/1977, riprendendo le affermazioni della giurisprudenza costituzionale, si riferiva esclusivamente ai «fatti eversivi dell’ordine costituzionale».

Un peculiare aspetto del diritto di i. è il cosiddetto diritto di cronaca (o ius narrandi), cioè il diritto di raccontare ciò che avviene ed eventualmente commentarlo. Oltre che dal segreto, esso è limitato dalla tutela dell’onore (a protezione del quale è stato previsto l’istituto della rettifica), della riservatezza, del buon costume, e, secondo alcuni studiosi, dello stesso ordine pubblico. Un’ulteriore limitazione al diritto di cronaca è contenuta nella cosiddetta par condicio (➔), dal momento che tale normativa, nel prevedere l’obbligo di assicurare parità di condizioni tra le forze politiche in occasione delle elezioni, incide inevitabilmente sulla stessa libertà di informare.

I. di garanzia

Comunicazione con la quale il pubblico ministero, durante le indagini preliminari, avvisa l’indagato e la persona offesa del reato per cui sta procedendo, che sta per compiere un atto cui il difensore ha diritto di assistere (atti garantiti). L’avviso contiene l’indicazione del fatto di reato, del luogo in cui è avvenuto e delle norme che si ritengono violate (art. 369 c.p.); contiene inoltre l’invito alla nomina di un difensore di fiducia e viene inviato per posta, in piego chiuso raccomandato con ricevuta di ritorno. Qualora ne ravvisi la necessità, ovvero l’ufficio postale restituisca il piego per irreperibilità del destinatario, il pubblico ministero può disporre che l’i. di garanzia sia notificata dalla polizia giudiziaria o dall’ufficio giudiziario, organi che curano la notificazione degli atti del pubblico ministero. L’omissione dell’i. di garanzia determina la nullità dell’atto di indagine garantito, perché impedisce l’intervento del difensore, di fiducia o d’ufficio, alle operazioni di esecuzione e di acquisizione dell’atto per cui si procede.

Economia

Riguardo alle teorie economiche dell’i., occorre ricordare che l’i. è stata implicitamente considerata da economisti come A. Smith (1776), A. Cournot (1843) e C. Menger (1871), ma fu solo in seguito, nell’economia dell’impresa, che si fece esplicito riferimento all’i., ritenendo la trasparenza del mercato, cioè la perfetta i., una delle caratteristiche principali della concorrenza perfetta. Ciò nonostante, è prevalentemente a partire dagli anni 1960 che si sono sviluppate, grazie a G.S. Stigler, G. Akerlof, S. Grossman, J. Stiglitz, M. Rotschild, le teorie economiche dell’i., le quali studiano il ruolo dell’i. nella formazione del prezzo e nell’equilibrio dell’economia.

L’i. asimmetrica rappresenta una delle tematiche più ricorrenti nell’ambito di queste teorie. Essa è riferita a una situazione in cui due parti hanno gradi diversi di informazione. Gli agenti economici meno informati utilizzano allora dei segnalatori in grado di fornire i. indirettamente; in tal senso, un prezzo elevato può essere indice, agli occhi del consumatore, di una qualità migliore. Anche la garanzia, che assicura la redistribuzione del rischio dell’acquisto tra acquirente e venditore, segnala la fiducia che quest’ultimo ripone nella qualità dei propri prodotti e pertanto una sua disponibilità a cambiarli o ad aggiustarli qualora fossero difettosi. Infine, la scelta di una determinata polizza assicurativa e del corrispondente premio indica quanto l’assicurato ritenga probabile il verificarsi dell’evento. La non gratuità dell’i. è ritenuta una delle cause principali dell’i. asimmetrica. Il costo dell’i. è costituito dal prezzo pagato per il servizio di i. da colui che è meno informato, oppure dal valore del tempo impiegato per l’ottenimento delle i. stesse. Come è sostenuto dai marginalisti, l’agente economico acquisirà i. fin quando il suo costo marginale non eguaglierà il suo valore marginale.

I mercati nei quali l’i. è ritenuta tra i fattori principali in grado di determinare le dinamiche delle variabili economiche sono numerosi. Nel mercato finanziario, per es., sono necessarie alla compravendita dei titoli i. sulla società, sui suoi concorrenti e sull’andamento del mercato stesso; al fine di arginare gli effetti dell’i. asimmetrica, numerosi ordinamenti giuridici puniscono l’insider trading, cioè l’abuso di i. riservate. Il mercato assicurativo si distingue, invece, in quanto è l’acquirente, ossia l’assicurato, colui che possiede maggiori i.; questi è motivato a mantenere l’asimmetria di i. in quanto la determinazione di premi diversi per stessi tipi di assicurazione dipende fortemente dal grado e dal tipo di i. detenute dall’assicuratore.

Un fenomeno legato alla i. asimmetrica è la cosiddetta selezione avversa. Questa avviene quando la parte meno informata tenta di risolvere il problema informativo attraverso una auto-segnalazione della controparte che finisce però per danneggiare il proponente stesso del contratto. Tipico è il caso del prestito bancario: l’erogante non ha una i. perfetta sulla solvibilità del cliente-contraente. La banca può essere allora tentata di chiedere un tasso di interesse più elevato rispetto al caso in cui il contratto venisse stipulato in condizioni di perfetta i. tra le parti. Attraverso il maggior tasso di interesse, il proponente tenta di selezionare solo i clienti maggiormente determinati a richiedere il prestito perché fortemente convinti della bontà del loro progetto di investimento. In altri termini, essere disposti a pagare un interesse più alto viene interpretato come un segnale di qualità della controparte. In realtà il maggior onere dovuto al più elevato tasso di interesse finisce per selezionare investitori con progetti di investimento maggiormente rischiosi, e quindi disposti a pagare un tasso maggiore. In altri termini, l’aumento del tasso di interesse che avrebbe dovuto portare a una selezione di clienti solvibili finisce per lavorare al contrario, in modo avverso, selezionando clienti caratterizzati da progetti di investimento a maggior rischio e quindi meno solvibili.

Filosofia

L’estetica informazionale è una teoria estetica di carattere scientifico costituitasi in Francia e poi in Germania negli anni 1950 a opera soprattutto di A. Moles e M. Bense. Situandosi in un complesso crocevia disciplinare (teoria dell’i., calcolo statistico-matematico, strutturalismo, psicologia della percezione, sociologia), trattando l’opera d’arte alla stregua di un messaggio trasmesso da un emittente (l’artista o il gruppo creatore) a un ricevente (il fruitore) tramite il canale delle sensazioni visive, tattili, acustiche ecc., e presupponendo la scomponibilità del messaggio stesso in unità elementari (repertorio di segni), l’estetica informazionale afferma che la quantità di novità o l’originalità del messaggio si può calcolare sulla base della minore o maggiore ricorrenza in esso di segni elementari già noti. L’intelligibilità del messaggio, pertanto, risulta inversamente proporzionale alla misura dell’i. (o quantità di novità) in esso contenuta: più un messaggio è comprensibile, meno è interessante, risultando, al limite, banale; maggiore è l’i. che contiene, minore diventa la capacità del destinatario di comprenderlo in una percezione globale. Da ciò l’interesse che, in un secondo momento, l’estetica informazionale ha mostrato per la nozione di ridondanza, grandezza la cui misura indica l’eccesso di segni necessario perché una certa quantità di originalità venga convogliata in un messaggio, senza che esso diventi totalmente incomprensibile.

Telecomunicazioni

Nel linguaggio scientifico, il termine i., dal significato originario di comunicazione, notizia, messaggio, è passato anche a un significato specifico, identificandosi non più con la comunicazione, ma con il contenuto della comunicazione, e divenendo così una grandezza misurabile; dei problemi relativi a questa grandezza si occupa la teoria dell’i. che, come teoria statistica della comunicazione, è nata dalle indagini compiute da numerosi ricercatori fin dai primi decenni del 20° sec. sul modo più economico e fidato di impiegare i mezzi di comunicazione (telefono, telegrafo, televisione). Queste ricerche, che procedono tuttora e assumono spesso un’impronta matematica piuttosto accentuata, ebbero una prima formulazione sintetica e originale nel 1948 da parte di C.E. Shannon, in seguito alla pubblicazione A mathematical theory of communication.

Definizione del termine

Se per i. si intende un contenuto di differenza relativa, di novità e di imprevedibilità di un messaggio intercorrente fra sistemi in relazione, in quanto tale messaggio si può distinguere da tutti gli altri possibili e in quanto a priori esso è probabile ma non certo, l’i. contenuta in un messaggio (suscettibile di quantificazione e di misura) dipende dalla storia passata e dalle capacità espressive e percettive dei sistemi interagenti; essa si ripartisce in ciascuno dei segnali impiegati per rappresentare il messaggio e questi segnali formano il codice tramite il quale l’emittente invia l’i. al destinatario attraverso una conveniente via di comunicazione. In generale per manifestarsi l’i. richiede un supporto materiale, che ne permetta il trasferimento o la conservazione, e un osservatore che la rilevi ed eventualmente la impieghi.

Il contenuto informativo di un messaggio può essere identificato con le differenze, di qualunque tipo, rilevabili tra le varie porzioni del supporto materiale del messaggio, oppure con l’aspetto specifico assunto dal supporto in quanto diverso da tutti gli altri aspetti a priori possibili. Alla rilevazione delle differenze da parte dell’osservatore (livello A o sintattico) può accompagnarsi la comprensione del loro significato (livello B o semantico), cioè la loro collocazione nel quadro della precedente esperienza dell’osservatore. Le differenze rilevate e comprese possono da ultimo essere impiegate dall’osservatore in vista dei propri fini (livello C o pragmatico); in questo caso le differenze presenti nel messaggio inducono differenze nell’osservatore, che così diventa a sua volta supporto d’informazione. Si osservi tuttavia che il momento pragmatico si presenta solo se l’i. ricavata dall’osservazione è utile, cioè se risponde a una domanda esplicita o implicita dell’osservatore.

L’i. consiste dunque in differenze capaci di indurre altre differenze lungo circuiti di comunicazione più o meno complessi, non sempre lineari e sovente dotati di rami di retroazione. Il punto del circuito informazionale, dove (spesso convenzionalmente) si stabilisce che abbiano origine le differenze destinate a propagarsi, si chiama sorgente d’informazione. Il meccanismo fisico o psicologico con cui la sorgente si colloca a un dato istante in un certo stato piuttosto che in un altro può essere anche assai complicato e in molti casi si è costretti a schematizzare l’attività della sorgente mediante una descrizione statistica. Questa descrizione, che è quasi sempre fortemente riduttiva, costituisce insieme il punto di partenza per tutti i risultati ottenuti dalla teoria matematica dell’i. e la sua limitazione fondamentale.

Una sorgente può generare un insieme molto ampio ed eterogeneo di informazioni. L’interesse o la capacità di osservazione di un dato osservatore possono orientarlo verso un sottoinsieme (talora molto esiguo) di tali informazioni. Per quell’osservatore la sorgente è costituita da quel sottoinsieme e la stessa sorgente appare diversa a diversi osservatori. In generale quindi più che di sorgenti è preferibile parlare di coppie, costituite da una sorgente e da un osservatore. Prima di rilevare lo stato assunto in un certo istante dalla sorgente è possibile che l’osservatore possegga un’idea più o meno precisa dell’insieme degli stati possibili e attribuisca a ciascuno stato un certo grado di attendibilità (che si può identificare con una probabilità a priori). L’osservazione dello stato effettivo può talora modificare l’insieme congetturato degli stati possibili e certamente modifica la loro distribuzione di probabilità, poiché lo stato osservato diviene certo e tutti gli altri impossibili.

Misura della quantità d’informazione

Definita l’i. come il complesso delle differenze rilevabili, si pone il problema quantitativo della sua misura. A questo fine possono essere definiti due casi, che corrispondono rispettivamente al livello A e ai livelli B e C, a seconda che degli eventi osservati interessino solo le differenze oppure anche il loro significato e utilità per l’osservatore. Il primo caso corrisponde all’i. selettiva ed è quello formalizzato da Shannon. La quantità d’i. fornita da un’osservazione relativa a un evento A_i si fa dipendere solo dalla sua probabilità prima dell’osservazione, p_i, e dalla sua probabilità dopo l’osservazione, p_i′, e viene espressa mediante la formula I(A_i) = log(p_i′/p_i). Si noti che non sempre un’osservazione relativa all’evento (o un messaggio sull’evento) contiene tutta l’i. necessaria per stabilire che l’evento si è prodotto oppure no; in altre parole non sempre un’osservazione rimuove tutta l’incertezza che presenta a priori il risultato di un’esperienza aleatoria. Quindi la probabilità a posteriori p_i′ non sempre è uguale a 1 o a 0. Si consideri come esempio l’esperienza ‘lancio di un dado’ e siano O₁ un osservatore capace di distinguere solo i due risultati ‘numero pari’ e ‘numero dispari’ e O₂ un osservatore capace di distinguere tutte e sei le facce del dado. Supponiamo che O₂ sia interessato all’evento A₃ = ‘viene 3’, ma che non possa osservare direttamente il risultato del lancio e debba accontentarsi del messaggio, comunicatogli da O₁, ‘è uscito un numero dispari’. Questo messaggio fornisce a O₂ una quantità d’i. su A₃ data da I′(A₃) = log(p₃′/p₃), dove p₃ = 1/6 è la probabilità a priori che esca 3 e p₃′ = 1/3 è la probabilità dello stesso evento dopo il messaggio di O₁. Dunque I′(A₃) =log2. Se il numero uscito fosse proprio 3, un’osservazione diretta di O₂ gli avrebbe fornito la quantità d’i. I(A₃) = log(p₃′/p₃), dove ora p₃′ = 1 e p₃ = 1/6. Dunque I(A₃) = log6 e si può concludere che da ogni osservazione diretta O₁ ricava log2 unità d’i., mentre O₂ ne ricava log6 poiché è capace di distinguere tra eventi più ‘fini’. L’incertezza totale che O₂ deve eliminare per conoscere i risultati che gli interessano è log6 = log2 + log3, mentre i messaggi che riceve da O₁ gliene eliminano solo log2; dopo un messaggio da O₁ l’incertezza residua di O₂ è pari a log3. Quando l’osservazione elimina tutta l’incertezza, la probabilità a posteriori dell’evento osservato A_i è 1. In tal caso la quantità d’i. recata dall’osservazione è I(A_i) = log(1/p_i) e si chiama autoinformazione dell’evento A_i. Se p_i = 1 (evento certo) il presentarsi di A_i non reca alcuna informazione, mentre se p_i ≃ 0 (evento molto improbabile), il presentarsi di A_i fornisce una quantità molto grande d’informazione.

La scelta della funzione logaritmo si adegua quindi a questa naturale richiesta di monotonia (inversa) dell’i. rispetto alla probabilità, ma soddisfa anche una notevole proprietà di additività che appare desiderabile per una misura della quantità d’informazione. Se degli eventi considerati non interessa solo l’aspetto combinatorio o probabilistico, ma anche l’utilità in rapporto ai fini dell’osservatore, si può assegnare una misura dell’i. utile, nella quale, accanto alla probabilità p_i dell’evento A_i interviene anche la sua utilità u_i, che è un numero non negativo assegnato dall’osservatore sulla base di considerazioni soggettive indipendenti dalla probabilità. L’autoinformazione utile dell’evento A_i è allora −u_ilogp_i e l’entropia utile di un’esperienza E che possa dare i risultati A₁, A₂, ..., A_k, dotati di probabilità p₁, p₂, ..., p_k e utilità u₁, u₂, ..., u_k, è espressa dalla formula

La teoria di Shannon

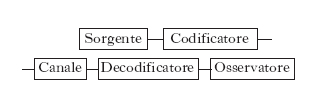
Come si è accennato, costituisce il nucleo più sistematico e formalizzato della teoria dell’i. e il suo oggetto di studio è, in prima approssimazione, il seguente modello semplificato di un sistema di generazione e trasmissione dell’i.:

L’ipotesi fondamentale è che sorgente, canale e osservatore sono assegnati una volta per tutte e che per migliorare le prestazioni del sistema si può agire solo su codificatore e decodificatore: essi debbono essere progettati in modo da fornire all’osservatore, con la precisione da esso desiderata, l’i. generata dalla sorgente compatibilmente con la presenza del rumore sul canale. Il codificatore elabora la successione di simboli o messaggi emessi dalla sorgente trasformandola dapprima in una successione per quanto possibile priva di ridondanza, in cui cioè ogni simbolo contenga al limite la massima quantità d’i. (un bit se la successione è binaria), e poi in una successione in cui ai precedenti simboli non ridondanti siano intercalati, con opportune regole, simboli ridondanti che assicurino una certa protezione contro i disturbi. Il decodificatore compie le operazioni inverse, ricostruendo per l’osservatore una stima (per quanto possibile corretta) della successione generata dalla sorgente (➔ codice). Il risultato fondamentale della teoria di Shannon si può enunciare così: data una sorgente di entropia H e un canale di capacità C alimentato da quella sorgente, se H < C si possono progettare un codificatore e un decodificatore tali che l’osservatore può ricevere tutta l’informazione generata dalla sorgente con una probabilità di errore per simbolo arbitrariamente piccola (se non si pone nessuna limitazione sulle risorse, per es. il tempo di elaborazione). Se invece H > C tale probabilità di errore non può scendere al di sotto di una quantità positiva, qualunque coppia di codificatore e decodificatore si impieghi. La prima parte del teorema, relativa al caso H < C, ha purtroppo solo carattere esistenziale e non costruttivo, cioè non indica come trovare i codici ottimi. Essa ha peraltro fornito una base sicura per tutto l’insieme delle ricerche che vanno sotto il nome di teoria dei codici.

I. e secondo principio della termodinamica

Le espressioni dell’entropia informazionale sono formalmente analoghe a quelle che, sulla base di considerazioni statistiche, si ricavano per l’entropia di un sistema costituito da un gas che possa assumere stati diversi con probabilità note (➔ entropia). Nella meccanica statistica il significato della funzione entropia non è ristretto alla sola termodinamica, poiché essa sta a indicare in generale il grado di indifferenziazione o disordine (in contrapposto a specializzazione od ordine) di un insieme statistico suscettibile di diverse configurazioni: nel caso termodinamico l’insieme statistico è quello delle diverse ‘complessioni’ del gas, mentre in teoria dell’i. è quello dei diversi possibili aspetti del supporto del messaggio. Il secondo principio della termodinamica, anch’esso da riguardare nel suo significato generale, afferma che l’evoluzione spontanea procede sempre in modo da far crescere l’entropia e quindi da far aumentare l’indifferenziazione. L’i. contenuta in un messaggio invece opera sempre in modo da ridurre il disordine, creando entropia negativa. In questo senso, dunque, l’i. si oppone all’evoluzione spontanea dei sistemi fisici verso l’uniformità indifferenziata, mentre per il secondo principio della termodinamica vi è una generale tendenza verso una continua degradazione dell’i., i cui effetti si osservano esplicitamente nell’azione del rumore sull’i. trasmessa in un canale. È dall’azione combinata e dall’equilibrio dinamico che si instaura tra questi due opposti principi che possono nascere e svilupparsi sistemi (come gli organismi) in cui la crescita della complessità e dell’ordine è spiegabile con una prevalenza, almeno temporanea, dell’i. sulla degradazione termodinamica.

Approfondimento:

L’accesso ad internet: un nuovo diritto fondamentale? di Roberta Pisa