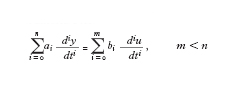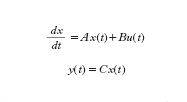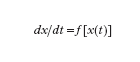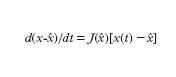complessità
complessità Caratteristica di un sistema (perciò detto complesso), concepito come un aggregato organico e strutturato di parti tra loro interagenti, in base alla quale il comportamento globale del sistema non è immediatamente riconducibile a quello dei singoli costituenti, dipendendo dal modo in cui essi interagiscono.
Biologia
Cellula, organismo pluricellulare, popolazione e comunità sono oggetti biologici graduati secondo un criterio di c. crescente. Negli ultimi anni 1990, si è cominciato a guardare alla complessità c. biologica come attributo non tanto dei sistemi viventi in sé, quanto delle rappresentazioni che la scienza dà dei sistemi viventi. Tra le tante conseguenze collegabili a questo mutamento di ottica se ne indicano qui due sole: l’attribuire la c. ai modelli di rappresentazione, implicati dalla relazione osservatore-osservato, piuttosto che agli oggetti in sé stessi, da una parte rimuove dall’attività di ricerca le eventuali preclusioni di ordine metafisico, rendendo i sistemi viventi conoscibili anche in via di principio, dall’altra pone i modelli biologici come modelli esplicativi spesso e in qualche misura irriducibili a quelli delle scienze fisiche. Rimanendo nel solco della visione tradizionale, che attribuisce la c. ai sistemi viventi piuttosto che alla loro modellizzazione, si può affermare che il carattere intrinsecamente complesso dei sistemi viventi concorre a fondare l’autonomia della biologia. L’organizzazione, l’individualità, la diversità, la relazionalità sono quattro caratteristiche comuni ai sistemi viventi e sono altrettante determinanti della loro complessità.
Organizzazione
Proprietà fondamentale di tutti i viventi è essere sistemi organizzati: possedere un’organizzazione significa presentare un certo insieme di relazioni che assicurano la coerenza interna del sistema. Queste relazioni sono responsabili dell’unitarietà dei sistemi viventi e del loro mantenimento. L’organizzazione dei viventi mostra di avere una natura gerarchica per cui gli organismi unicellulari, quelli pluricellulari, le popolazioni e le biocenosi si presentano come entità caratterizzate da configurazioni strutturali e da dinamiche processuali differenti a ciascun livello e dotate di proprietà né immediatamente deducibili né prevedibili. Oltre che gerarchica tale organizzazione è anche chiusa, grazie all’innesco di circolarità in meccanismi altrimenti lineari di causa ed effetto. La logica circolare (ben esemplificata dal rapporto causale: gameti-zigote-gameti) percorre tutti i livelli della gerarchia, dalla cellula all’ecosistema. I sistemi viventi sono sistemi chiusi rispetto alla loro organizzazione interna ma sono sistemi aperti sull’esterno, con il quale scambiano materia, energia, informazione. Ogni organismo è necessariamente connesso con l’ambiente e tale connessione è talmente obbligata che diventa impossibile anche solo concepire l’esistenza di un organismo isolato o isolabile dal proprio ambiente.
Individualità
I sistemi viventi non sono ripetitivi: l’eterogeneità è la norma. Tanto sul piano strutturale che su quello funzionale, i sistemi viventi sono distinguibili dai sistemi non viventi naturali sulla base della loro individualità. Di norma ogni vivente possiede una propria individualità (una unicità originariamente dovuta alle proprietà stocastiche della sorgente di variazione) che viene codificata nei geni, viene costruita epigeneticamente e viene trasmessa alla progenie. All’interno di ciascun deme, la somma delle individualità si traduce nell’assetto della variazione genetica mediante cui la popolazione nel suo insieme fronteggia le richieste dell’ambiente. L’unicità degli individui diventa essenziale per l’adattamento della popolazione a un ambiente perennemente mutevole. La stragrande maggioranza dei sistemi viventi può essere costituita non solo da entità tra loro intrinsecamente, cioè genotipicamente, diverse ma può anche essere formata da subunità strutturalmente eterogenee e che hanno quindi comportamenti che seguono leggi differenti l’una dall’altra. È il caso del corredo di proteine enzimatiche di una cellula, o quello dei diversi tipi di cellule costitutive del corpo dei Vertebrati. In sostanza la c. biologica è riferita a sistemi di tipo individuale, cioè non ripetitivo, per i quali valgono leggi specifiche. Da ciò deriva un’importante conseguenza di ordine teorico generale: la non universalità delle leggi ricavabili dalle descrizioni dei sistemi biologici ha reso estremamente difficile l’applicabilità dei metodi matematici deterministici ai fenomeni biologici. Un’ulteriore osservazione è che l’individualità dei sistemi biologici ha duplice natura: è concausa di evoluzione e prodotto storico dell’evoluzione.
Diversità
Differenze di vario ordine e grado sottostanno alla complessità. Indipendentemente dagli effetti di scala, la diversità dei sistemi viventi deriva dalla loro individualità e concorre a definirne la complessità. Globalmente, la biodiversità è costituita dall’insieme delle differenze osservabili tra gli esseri viventi. Tali differenze possono essere descritte in termini di quantità, di variazione e di variabilità degli organismi; nonché, semplificando, in rapporto ai geni, alle specie e agli ecosistemi. In particolare, la diversità genetica è rappresentata da tutte le differenze ereditabili esistenti tra gli individui in una popolazione (e tra le diverse popolazioni) e che sono riconoscibili a livello genico. La diversità genetica è riconducibile, in ultimo, alle differenze di sequenza nelle coppie di basi degli acidi nucleici. Negli organismi dotati di sessualità, le novità genetiche comparse per mutazione possono diffondersi nella popolazione mediante ricombinazione, un dispositivo capace di generare un immenso numero di differenze. La struttura e il numero dei cromosomi, come pure la quantità di DNA contenuta in una cellula, sono esempi di diversità genetica. In particolare, la quantità di DNA contenuta in una cellula (dimensione del genoma) permette di confrontare organismi di taxa di livello anche assai superiore a quello di specie. Nei batteri, per es., le dimensioni dei genomi variano ampiamente da 6×105 bp (paia di basi) a più di 107 bp. Il genoma del micoplasma è formato da circa 400 geni, mentre negli altri batteri il numero di geni varia tra 500 e 8000. La maggioranza degli Eucarioti possiede, invece, qualcosa come 50.000 geni e un contenuto di DNA estremamente differente, variabile tra 8,8×106 bp e 6,9×1011 bp. Evolutivamente, la comparsa della sessualità ha provocato un incremento della diversità genetica e della c. dei sistemi viventi. La sua enorme diffusione tassonomica viene interpretata come dispositivo di riparazione del DNA e come meccanismo che permette il differenziamento cellulare, la produzione di varianti genetiche adattabili per via fenotipica ai cambiamenti ambientali, l’incremento della cladogenesi, il decremento dei tassi di estinzione; in sostanza la sessualità sembra essere importante perché può agire ed essere favorita a molti livelli di organizzazione dei sistemi viventi, da quello di gene a quello di popolazione-specie.
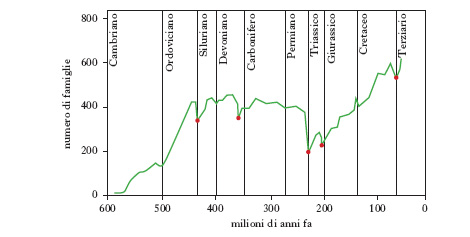
La diversità tassonomica di specie, oltre alla componente spaziale, geografica, ha una componente temporale. La diversità oggi osservabile è il risultato di un processo storico lunghissimo iniziato tra 3900 e 3400 milioni di anni fa con la comparsa della vita sul pianeta. Tale processo di produzione delle differenze tra i viventi ha natura irreversibile. La ricostruzione paleontologica dimostra il fatto che la diversità macrotassonomica (intesa come ricchezza di tipi organizzativi, fig. 1) raggiunse il suo apice nel Cambriano e che la diversità di famiglia e di specie è andata aumentando dal Cambriano al Pleistocene con poche battute d’arresto, in corrispondenza delle fasi, brevi e isolate, di estinzione di massa (v. in fig. 2 la diversità biologica nel tempo per gli animali marini). Le differenze ecologiche, e quindi la c. ecologica degli ecosistemi, sono le più difficili da definire perché di norma le comunità e gli ecosistemi sono entità dai contorni sfumati, gli ecosistemi non sono entità esclusivamente biologiche ma includono anche componenti abiotiche e infine perché esiste un fattore di scala spazio-temporale che influenza pesantemente l’osservazione, la misurazione e l’interpretazione delle differenze sia intra- sia interecosistemiche.
Relazionalità
La possibilità comprovata per certi sistemi non viventi (per es., le celle di Benard o la reazione di Belousov-Žabotinskij: ➔ autoorganizzazione) di passare spontaneamente da condizioni di tipo caotico a stati di tipo ordinato ha indotto molti ricercatori a ritenere che processi analoghi fossero responsabili dell’organizzazione dei sistemi viventi e del suo incremento. L’analogia tra i sistemi complessi di tipo fisico o chimico e quelli biologici è però solo superficiale, perché nei sistemi biologici l’elemento di ordine capace di organizzare le componenti eterogenee del sistema è rappresentato da relazioni che promuovono l’interconnessione tra le parti. Tali relazioni hanno la forma di un segnale. Attraverso segnali le cellule di una coltura batterica o le componenti di un sistema pluricellulare trasferiscono informazione dall’una all’altra, coordinando i processi interni con quanto accade all’esterno di ciascuna di esse. A livello degli organismi pluricellulari, il sistema costituito dal segnale e dal suo recettore non solo assicura l’integrazione tra le varie cellule, per es. durante i processi di sviluppo, ma negli animali può anche consentire l’integrazione sociale degli individui sia attraverso l’azione degli ormoni, sia attraverso quella dei neurotrasmettitori. In tutti i gruppi di organismi si assiste a una diversificazione della coppia segnale-recettore. Tale diversificazione evolutiva produce sia una complicazione del sistema sia una sua compartimentalizzazione, con la localizzazione, in alcune regioni del corpo, delle cellule contenenti i differenti recettori. Inoltre, se da una parte l’evoluzione filogenetica della coppia segnale-recettore ha la funzione di rendere più efficiente e affidabile l’integrazione tra gli individui (con ciò aumentando la diversità interna, intrasistemica, dei sistemi viventi), dall’altra essa serve a mantenere isolati sistemi tra loro incompatibili e in competizione (favorendo così la diversità esterna, intersistemica). I segnali coinvolti nel comportamento e responsabili della produzione delle barriere interspecifiche di isolamento riproduttivo pre-copula esemplificano puntualmente la funzione di mantenimento e incremento della diversità intersistemica e illustrano, a un livello assai elevato di c., quale sia la natura delle ‘forze’ che determinano la dinamica dei sistemi viventi.
Negli animali dotati di un sistema nervoso e di un cervello sufficientemente complesso, il sistema segnale-recettore è ancora all’opera nel consentire l’apprendimento e dunque, ricorsivamente, la generazione di meccanismi di produzione di diversità e di c. più sofisticati. E infine, riferendosi a un altro ambito fenomenologico, è sempre la capacità relazionale dei sistemi viventi a essere chiamata in causa nell’elaborazione epigenetica dell’informazione genomica nei processi di riconoscimento immunitario, nella morfogenesi, nell’ontogenesi del comportamento.
Tendenze evolutive e complessità
L’ordinamento di c. crescente (cellula procariote, cellula eucariote, organismo pluricellulare, popolazione, comunità, ecosistema) di solito si accompagna all’idea che nella storia della vita sul pianeta sia riconoscibile una tendenza verso la crescita della c. dei sistemi viventi. Per quanto suggestiva, questa convinzione si dimostra errata perché se è indiscutibile che le forme organizzative più semplici hanno preceduto di norma quelle più complesse, tuttavia la coesistenza temporale di forme poco complesse accanto a forme molto complesse testimonia non la sostituzione di sistemi meno complessi con sistemi più complessi ma la coesistenza di sistemi a vario grado di complessità. Inoltre, è noto che nel corso dell’evoluzione vi sono stati molti casi in cui i sistemi viventi sono andati incontro a processi di drastica semplificazione di alcune subunità, dunque a una riduzione della loro c. generale. È il caso, per es., della semplificazione anatomica dell’occhio, fino alla sua scomparsa totale e definitiva negli animali ciechi e anoftalmi che vivono negli ambienti cavernicoli. Un’evoluzione regressiva analoga è presentata dai parassiti intestinali, nei quali si assiste, tra l’altro, alla perdita dell’apparato digerente.
C. biologica e storia
Uno degli aspetti più ricchi di conseguenze, sebbene immediatamente non appariscente, dei sistemi viventi è quello di essere sistemi non universalmente necessitati, nel senso che le loro strutture e i loro comportamenti non sono descrivibili con leggi universali bensì da enunciati validi per casistiche spesso assai limitate. Da cosa derivi questa caratteristica è facilmente comprensibile considerando alcuni esempi quantitativi che illustrano un peculiare aspetto dei sistemi viventi: l’enorme discrepanza tra quanto è teoricamente possibile su base combinatoria e quanto invece si è storicamente realizzato. Il fatto, invece, che di tutte le possibili combinazioni genotipiche solo alcune effettivamente si siano realizzate e solo alcune si realizzeranno rappresenta una chiara evidenza della natura relativa e contingente dei sistemi biologici. È questa contingenza a fondare la natura storica dei viventi: la c. osservabile deriva da vincoli strutturali e funzionali preesistenti che a loro volta determinano la dinamica futura dei sistemi. Non tutti i cammini evolutivi sono dunque possibili ma solo quelli compatibili con il regime di vincoli esterni e interni al sistema. I sistemi viventi sono entità storicamente determinate e la biologia assume anch’essa carattere storico ogni volta che si pone problemi che vanno oltre il comportamento delle molecole.
Fisica
Al fine di valutare la c. di un sistema non sembra essenziale tanto il numero delle parti che lo compongono quanto invece il modo, più o meno organico, in cui queste interagiscono. Spesso, a tal proposito, si ricorre alla valutazione di due parametri: K (imprevedibilità del comportamento) e Q (organizzazione del sistema). Il parametro K dà conto della possibilità o meno di prevedere l’evoluzione temporale su intervalli più o meno lunghi, partendo da dati inevitabilmente affetti da qualche incertezza. Per K uguale a zero il comportamento del sistema è perfettamente prevedibile (caso di sistemi statici o di sistemi che evolvono secondo leggi deterministiche semplici); per valori di K molto elevati l’informazione sul comportamento del sistema si perde molto rapidamente e ciò rende di fatto impossibile, se non in termini probabilistici, la previsione dello stato del sistema a un certo istante, pur essendo noto quello a un istante precedente, anche molto prossimo. Un sistema caratterizzato da un valore di K vicino a zero è, per es., il sistema Sole-Terra, nel quale la posizione e la velocità della Terra a un certo istante sono determinabili a partire dai valori (affetti da inevitabili incertezze) che tali grandezze avevano a un istante precedente, anche piuttosto remoto. Un sistema caratterizzato invece da un valore elevato di K è, per es., un gas perfetto in uno stato di equilibrio termodinamico, nel quale minime incertezze sui valori di posizione e di velocità delle singole molecole a un certo istante rendono inattendibili le stime di tali valori dopo un intervallo di tempo anche brevissimo, a causa degli urti fra molecole, che hanno luogo in corrispondenza di certi valori delle suddette grandezze ma non per valori anche pochissimo diversi. Valori intermedi di K possono corrispondere ai cosiddetti fenomeni di caos deterministico. Il parametro Q dà invece conto dell’organizzazione del sistema, cioè della struttura secondo la quale le varie parti componenti si influenzano reciprocamente, consentendo un comportamento caratterizzato da scelte funzionali al conseguimento di obiettivi, anche in presenza di più obiettivi incompatibili. Il valore più elevato di Q, fra i sistemi noti, si ha nel caso del cervello umano. Va notato che né a K né a Q è attribuibile, per un dato sistema, un preciso valore e in tal senso la caratterizzazione della c. mediante questi parametri è qualitativa. Generalmente è però possibile, confrontando due sistemi, precisare se il valore di K (o di Q) di uno di essi sia superiore o inferiore al valore dello stesso parametro per l’altro sistema. All’aumentare del numero delle parti che compongono un sistema, generalmente K aumenta, mentre si può avere un incremento di Q, a parità di un numero di parti componenti, in conseguenza di una modifica della struttura del sistema che lo porti a un’organizzazione meglio articolata; peraltro, valori elevati di Q possono essere conseguiti solo se il numero delle parti componenti non è troppo basso.
Dal punto di vista della fisica, l’obiettivo da raggiungere nello studio dei sistemi complessi consiste nel trovare le leggi fenomenologiche che regolano il comportamento globale di tali sistemi, non facilmente deducibili dall’analisi delle leggi che regolano i singoli costituenti. Un sistema complesso può essere descritto sia a livello dei singoli componenti sia a un livello globale più alto, in cui si rende necessario l’impiego di categorie e concetti del tutto diversi. Così, per es., il comportamento dei singoli neuroni può ritenersi compreso in modo soddisfacente, ma non è chiaro perché 10 miliardi di neuroni, collegati da 100.000 miliardi di sinapsi, formino un cervello che pensa. In certi contesti la comparsa di comportamenti collettivi è un fenomeno ben studiato dalla fisica: la cooperazione di molti atomi e molecole è responsabile delle transizioni di fase (come liquido-solido o liquido-gas). Quando un sistema assume più di una fase può essere descritto dal punto di vista macroscopico specificando in quale fase esso si trovi (solida, liquida o gassosa). Normalmente nei sistemi fisici, a una data temperatura e a una data pressione, il numero delle fasi è piccolo (nell’acqua possono coesistere in equilibrio uno, due o al massimo tre stati di aggregazione), cosicché la descrizione macroscopica è molto semplice. Al contrario, se si esamina un sistema biologico, che può essere considerato come il prototipo di un sistema complesso, la sua descrizione macroscopica è generalmente molto più articolata, varia e ricca (un animale può dormire, mangiare, correre ecc.). Anche la varietà dei dati necessari per la descrizione macroscopica di un sistema può essere presa come indicatore della sua complessità.
A prima vista potrebbe sembrare che tutti i sistemi fisici tradizionali siano semplici e che la c. sia esclusa dal mondo della fisica ma, particolarmente negli ultimi decenni del 20° sec., sono stati trovati molti sistemi caratterizzati da una notevole c., anche dal punto di vista della ricchezza nella descrizione macroscopica: alcuni tipici esempi sono i sistemi amorfi, i vetri di spin, le interfacce e le reti neurali.
Informatica
complessità C. computazionale Disciplina che studia la misura delle difficoltà incontrate nel risolvere le varie classi di problemi che si presentano nelle più diverse applicazioni. Nata attorno al 1970, tale disciplina ha avuto un rilevante sviluppo con l’estendersi dell’uso dei calcolatori e le conseguenti crescenti esigenze di mettere a punto procedure o algoritmi per risolvere i più diversi problemi.
Un aspetto particolarmente interessante della c. computazionale è la valutazione di un dato algoritmo concepito per risolvere una assegnata classe di problemi. L’efficienza di un algoritmo viene valutata in genere considerando il numero di operazioni elementari (somme e confronti) richieste per la soluzione di un dato problema. Da tale numero, assegnato un dato tipo di calcolatore, è possibile risalire al tempo di elaborazione necessario per risolvere il problema. Un secondo parametro di una certa importanza, che viene spesso preso in considerazione, è lo spazio di memoria richiesto dall’algoritmo. Nella definizione di efficienza sorgono però alcuni problemi concettuali. Una classe di problemi comprende molti problemi particolari, spesso un numero infinito. D’altra parte il tempo di calcolo di un algoritmo è definito rispetto a un problema particolare (detto anche istanza) e sarà in generale diverso per istanze diverse anche se appartenenti alla stessa classe. È abbastanza complesso definire l’efficienza di un algoritmo rispetto a una data classe di problemi; in particolare ciò può essere fatto scegliendo una o più istanze, appartenenti alla classe, rispetto alle quali valutare l’efficienza.
Un altro aspetto interessante della c. computazionale è rappresentato dalla possibilità di valutare la c. di una classe di problemi indipendentemente dall’algoritmo usato per risolverli, cioè poter fare affermazioni del tipo: data quella particolare classe di problemi, qualsiasi algoritmo sia possibile costruire in pratica avrà un’efficienza di un tipo assegnato. La tecnica più diffusa per misurare l’efficienza di un algoritmo è basata sulla valutazione asintotica nel caso peggiore. Tale tecnica consiste nel valutare, per ogni fissata dimensione L di un’istanza della classe considerata (dimensione data, per es., dal numero di bit necessari per la memorizzazione), il tempo necessario all’algoritmo per risolvere la più difficile istanza della classe e nello studiare il comportamento asintotico (cioè per L che tende all’infinito) di questo parametro. Da un punto di vista formale, sia R il problema considerato (insieme di tutte le possibili istanze del problema), R(L) (con L intero positivo) l’insieme di tutte le istanze di dimensione L e t(a, p) il tempo di calcolo necessario all’algoritmo a per risolvere l’istanza p ∈ R. Indichiamo con τ(L) il seguente valore:
La tecnica della valutazione asintotica del caso peggiore consiste pertanto nello studiare l’andamento della funzione τ(L) per L che tende all’infinito, in pratica per L sufficientemente grande da non essere più influenzato in modo significativo da eventuali pre-elaborazioni richieste dall’algoritmo indipendenti dalla dimensione del problema. Di fatto, la determinazione di τ(L) è molto complessa e possibile solo in pochissimi casi. Quello che viene valutato è normalmente una funzione g(L) tale che τ(L) ≤ g(L) per L > L′, con L′ abbastanza grande, e, ove possibile, una funzione g′(L) tale che τ(L) ≥ g′ (L) per L > L′. Naturalmente quello che in pratica interessa di più è stabilire l’ordine di crescita di τ(L), cioè trovare una funzione g(L) tale che τ(L) ≤ g(L); infatti tale funzione fornisce un limite superiore al tempo di calcolo e permette di dare garanzie in sede progettuale sul tempo massimo entro il quale si ottiene comunque una risposta. L’andamento del limite inferiore è meno significativo perché, essendo una valutazione di tempo minimo richiesto nel caso peggiore, niente dice sul tempo richiesto per una specifica istanza.
Spesso per ragioni di comodità e di immediatezza nel leggere un risultato, si studia, anziché l’andamento τ(L) rispetto alla dimensione L delle istanze, un andamento τ(k) rispetto a un qualche parametro k strettamente collegato a L (o a più parametri legati a L). Nel tentativo di caratterizzare in modo sintetico l’andamento della funzione τ(L) vi è un elemento che viene considerato con particolare attenzione e che induce una prima classificazione degli algoritmi. Una prima possibilità è che τ(L) sia una funzione polinomiale di L o sia limitata superiormente da una funzione polinomiale in L. Una seconda possibilità è che non esista nessun polinomio in L di grado finito che fornisca un limite superiore a τ(L) per L crescenti; questo è, per es., il caso in cui τ(L) è una funzione esponenziale di L. Questa prima classificazione tra algoritmi polinomiali ed esponenziali, pur se di notevole interesse, lascia aperti vari interrogativi. Infatti disponendo per un problema di un algoritmo esponenziale, ci si può chiedere se con poco sforzo non sia possibile trovare per lo stesso problema un algoritmo polinomiale. Per poter dare una risposta a tale interrogativo è stata introdotta una classificazione dei problemi in classi di complessità che fornisce utili indicazioni sul tipo di algoritmi che ragionevolmente può essere trovato per risolvere il problema in esame.
Limitandoci ai problemi polinomiali, possiamo introdurre le classi P e NP di problemi. Un problema è detto polinomiale (o che appartiene alla classe P dei problemi polinomiali) se esiste un algoritmo che fornisce la risposta in tempo polinomiale rispetto alle dimensioni L del problema. Un problema è detto NP (che appartiene alla classe NP) se una macchina di Turing non deterministica è in grado di risolverlo in tempo polinomiale. Dati ora due problemi R e Q si dice che «R si riduce a Q» (e si indica con R ∝ Q), se esiste un algoritmo polinomiale che associa a ogni istanza di R un’istanza di Q in modo tale che la soluzione dell’istanza di Q fornisce la soluzione della corrispondente istanza di R. Un problema R ∈ NP si dice NP-completo se Q ∝ R per ogni Q ∈ NP. In altre parole i problemi NP-completi sono i problemi più difficili della classe NP. Il problema che ora si pone è quello di stabilire se la classe NP è effettivamente più generale di P o si tratta invece della stessa cosa. Questa domanda è oggi senza risposta, infatti il problema se P ∕= NP oppure no, è uno dei maggiori problemi aperti nel settore algoritmico. La congettura che viene comunemente accettata è che sia P ∕= NP. Se si trovasse un algoritmo in grado di risolvere in tempo polinomiale un problema NP-completo, allora, per la definizione di NP-completezza, si potrebbe usarlo per risolvere velocemente tutti i problemi NP, dimostrando la coincidenza delle due classi P e NP. Da un punto di vista operativo per dimostrare che un problema R è NP-completo basta prendere un problema NP-completo noto e costruire una riduzione da questo problema a R. A causa della transitività della riduzione ciò basta per affermare che anche R è NP-completo.
L’importanza pratica di tutto ciò risiede nella seguente considerazione: se si presenta un problema R per cui viene proposto un algoritmo esponenziale, il tentativo naturale sarebbe quello di cercare un algoritmo migliore di tipo polinomiale; questo tentativo può però essere privo di sbocco, poiché se viene dimostrato che il problema è NP-completo, è estremamente difficile che si possa trovare un algoritmo polinomiale (per quanto detto, equivarrebbe a dimostrare che P = NP). Quindi il suggerimento per il progettista di algoritmi è quello di fare alcuni tentativi per costruire un algoritmo polinomiale e, se questi falliscono, tentare di dimostrare la NP-completezza del problema. Nel caso in cui il problema sia NP-completo e l’algoritmo esponenziale non sia praticabile, sarà necessario ripiegare su tecniche euristiche che, nella migliore delle ipotesi, forniscono soluzioni approssimate. È bene tenere presente che questi concetti hanno sempre una validità relativa; infatti, trattandosi di valutazioni di tipo asintotico possono essere poco significative per le dimensioni reali del problema con cui si ha a che fare. In genere si riescono a risolvere problemi polinomiali per dimensioni anche molto elevate e si riescono a risolvere problemi NP-completi in modo esatto solo in pochi casi di dimensioni non molto elevate.
Matematica
Per quanto riguarda gli aspetti matematici dei metodi utilizzati per lo studio dei sistemi complessi, un primo livello, certamente molto elementare, di c. si manifesta nei sistemi che presentano un anello di retroazione (feedback; ➔ sistema). Per illustrare questo concetto si può far riferimento a semplici sistemi che sollecitati da ‘ingressi’ variano di conseguenza le ‘uscite’ (grandezze che caratterizzano il sistema). In un sistema dinamico il valore delle uscite in ciascun istante dipende dai valori degli ingressi anche in altri istanti. Nel caso dei sistemi dinamici lineari e a parametri costanti nel tempo, detti y(t) l’uscita, u(t) l’ingresso (considerati per semplicità scalari), x(t) il vettore di stato (a n componenti), il comportamento di un sistema può essere descritto, in termini di legami ingresso-uscita, dalle equazioni
dove A è una matrice, B è un vettore colonna e C un vettore riga. Per n=2, cioè quando lo stato del sistema è descritto da due scalari x1(t), x2(t), si ha
ovvero
Queste equazioni mostrano come lo stato del sistema all’istante t e il valore dell’ingresso nello stesso istante influenzino la tendenza a variare dello stato (cioè il valore della derivata rispetto al tempo del vettore di stato) e come l’uscita y(t) dipenda, tramite il vettore C, dal valore assunto nello stesso istante dal vettore di stato. Per semplicità ci si può limitare allo studio del caso in cui u(t)=0 (evoluzione libera), nel quale si ha una sola situazione di equilibrio per i valori di y e delle sue derivate nulli (sono quindi nulle tutte le componenti di x).
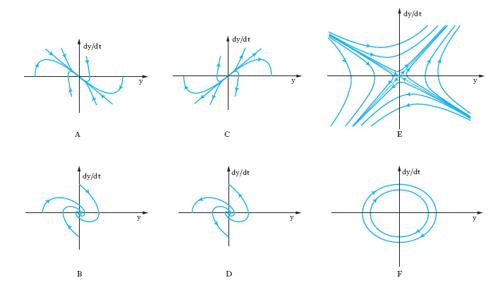
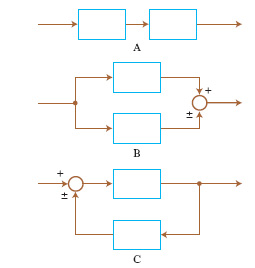
Per un sistema del secondo ordine (n=2), l’evoluzione libera a partire da uno stato di non equilibrio può essere descritta (oltre che con i diagrammi delle componenti di x in funzione del tempo) nel quadro di fase, il piano di coordinate y e dy/dt. Sei andamenti tipici di evoluzione libera nel quadro di fase nell’intorno di punti di equilibrio sono riportati in fig. 3. Se si collegano tra loro due sistemi lineari a un ingresso e a un’uscita in modo da formare un nuovo sistema lineare (anch’esso a un solo ingresso e a una sola uscita), semplicemente sommando o sottraendo grandezze di ingresso e/o di uscita, gli schemi possibili sono quelli riportati in fig. 4. Nei primi due (combinazione in cascata e in parallelo o antiparallelo) l’evoluzione del sistema rimane essenzialmente quella dei due sistemi componenti. Invece nel terzo tipo di collegamento (in cui è presente un anello di retroazione positiva o negativa) l’evoluzione del sistema complessivo risulta diversa da quella dei sottosistemi componenti. Anche se le parti componenti presentano dinamiche molto semplici, addirittura entrambe dello stesso tipo, ciò non di meno il sistema complessivo presenta un’evoluzione diversa da quella delle singole parti e di uno qualunque dei tipi illustrati in fig. 3. In tal senso emerge quindi un comportamento del sistema complessivo nuovo rispetto a quello delle parti componenti. J.W. Forrester attribuisce il comportamento antintuitivo dei sistemi complessi proprio alla presenza di anelli di retroazione. Modelli puramente lineari si sono però mostrati inadeguati nella descrizione della maggior parte dei sistemi complessi ed è stato giocoforza introdurre la non linearità come possibile causa dell’emergere di nuovi tipi di comportamento. Se la prima delle precedenti equazioni (con u(t)=0) viene sostituita con un’equazione del tipo dx/dt=f[x(t)] si ha che, a differenza del caso lineare in cui si aveva un solo punto di equilibrio in x=0 e questo per n=2 poteva essere soltanto dei tipi indicati in fig. 3, si possono avere più punti di equilibrio.
Un altro comportamento nuovo che emerge in presenza di non linearità consiste nell’esistenza di insiemi limite diversi dai punti di equilibrio. Gli insiemi limite più comuni sono cicli e tori (superfici toroidali). I cicli limite si possono avere in sistemi almeno del secondo ordine e corrispondono a traiettorie chiuse (e quindi a oscillazioni persistenti) relative a un’evoluzione temporale periodica ma non necessariamente sinusoidale. Nel caso di cicli limite stabili le traiettorie che partono da punti non appartenenti al ciclo (in un suo conveniente intorno) convergono su di esso, mentre nel caso dei cicli instabili ne divergono. Punti di equilibrio, cicli limite e superfici toroidali costituiscono le forme più semplici e comuni di insieme limite. Se tutte le traiettorie che escono da punti di un loro intorno tendono a essi, tali insiemi limite si dicono attrattori e l’intorno si dice bacino di attrazione; se invece le traiettorie tendono ad allontanarsi dall’insieme limite, pur partendo da punti molto prossimi a esso, l’insieme limite è detto repulsore. Vi sono anche insiemi limite che non sono né attrattori né repulsori. Uno stesso sistema non lineare può presentare più attrattori e repulsori.
Ulteriori aspetti del comportamento del sistema emergono se l’equazione che caratterizza la non linearità può essere scritta nella forma dx(t)/dt=f[x(t), p], dove p è un vettore le cui componenti sono parametri indipendenti dal tempo (o che variano molto lentamente in rapporto ai tempi caratteristici della dinamica del sistema) che influenzano i coefficienti delle equazioni del sistema. In tal caso, l’analisi del sistema può essere condotta valutando, nello spazio dei parametri, gli aspetti complessivi del comportamento del sistema, quali la presenza o meno di determinati insiemi limite e le loro caratteristiche.
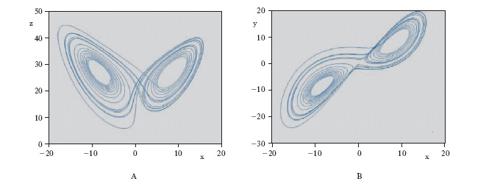
Si parla di stabilità strutturale di una data regione dello spazio dei parametri se al suo interno il comportamento del sistema rimane qualitativamente dello stesso tipo (per es., un ciclo limite rimane un ciclo limite, un nodo stabile rimane un nodo stabile ecc.). Situazioni particolari emergono nei punti di frontiera di tali regioni, detti punti di biforcazione (➔ biforcazioni, teoria delle), perché nel loro intorno si hanno punti dello spazio dei parametri arbitrariamente vicini fra loro cui corrispondono sistemi dinamici con caratteristiche essenzialmente diverse tra loro. Nello studio dei fenomeni di perdita della stabilità strutturale si è fatto largo impiego di nozioni della teoria delle catastrofi. All’aumentare dell’ordine n del sistema e quindi delle dimensioni del suo vettore di stato emergono fenomeni di caratteristiche più complesse in corrispondenza con l’apparire di attrattori strani, cioè di insiemi limite attrattivi sostanzialmente diversi dai punti di equilibrio, dai cicli e dai tori stabili caratterizzabili (secondo taluni autori) sulla base della forte sensibilità alle condizioni iniziali e alla dimensione frattale. Un attrattore strano (uno dei più semplici e più noti è l’ attrattore di Lorenz, schematizzato in fig. 5) è generalmente confinato in una regione limitata dello spazio di stato, mentre il suo bacino di attrazione occupa una regione assai più estesa (talora l’intero spazio). Dai punti del bacino di attrazione esterni alla regione dell’attrattore evolvono traiettorie che si dirigono verso di esso in modo non troppo diverso da quello con il quale tenderebbero a un attrattore di tipo più semplice; quando però la traiettoria entra nella regione dell’attrattore, essa evolve in modo sostanzialmente diverso da quello che caratterizza i cicli e i tori. Più precisamente, due traiettorie passanti per punti molto vicini (per es., tali che la loro distanza sia inferiore all’inevitabile errore di misura) continuano a essere vicine fuori dalla regione dell’attrattore strano ma, una volta giunte in essa, si allontanano ben presto notevolmente l’una dall’altra, tanto che il punto di una di esse, a un dato istante, può trovarsi prossimo alla frontiera della regione che include l’attrattore mentre il punto dell’altra, allo stesso istante, si può trovare al centro della regione o anche in una posizione diametralmente opposta a quella del primo.
Poiché la regione dell’attrattore è limitata, i punti corrispondenti a uno stesso istante sulle due traiettorie dovranno poi inevitabilmente riavvicinarsi, e poi allontanarsi di nuovo, ma senza dar luogo a un comportamento periodico o quasi-periodico. Nel caso di comportamenti di questo tipo si parla generalmente di caos deterministico: infatti il sistema è rigidamente deterministico (in quanto retto da equazioni come quelle considerate, prive di alcun elemento stocastico legato a variazioni di parametri o a sollecitazioni esterne descrivibili in termini probabilistici) e, ciò non di meno, il comportamento del sistema appare caotico (nel senso di imprevedibile) in quanto minime incertezze nella valutazione dello stato presente si traducono ben presto in differenze molto elevate dello stato futuro (pur in assenza di divaricazioni crescenti delle traiettorie, quali si hanno nei sistemi instabili, dato che l’attrattore è racchiuso in una regione limitata).
I principali meccanismi di passaggio al caos per modifiche graduali dei parametri di sistemi non caotici sono, fondamentalmente, una cascata di biforcazioni locali oppure una sola biforcazione, ma di carattere globale. Come si è visto, si manifestano fenomeni sostanzialmente nuovi e, quindi, emergono aspetti di comportamento che autorizzano a parlare di successivi livelli di c.: quando si ricorre a combinazioni in retroazione con le quali gli autovalori del sistema lineare complessivo risultano diversi da quelli delle parti componenti; quando si sostituiscono, a relazioni lineari, relazioni non lineari per effetto delle quali si manifestano insiemi limite, attrattori o repulsori, diversi dai classici punti di equilibrio dei sistemi lineari; quando variazioni di parametri provocano la comparsa di fenomeni di biforcazione alle frontiere delle regioni di stabilità strutturale; infine, quando si manifestano le tipologie più complesse di attrattori che danno luogo al caos deterministico.
Scienze sociali
C. sociale Seguendo N. Luhmann e A.S. McFarland, la c. sociale rappresenta la c. rilevabile all’interno di un sistema sociale, valutata in base al numero delle sue componenti, alla loro varietà, alla loro variabilità nel tempo e all’ampiezza e incidenza delle loro relazioni. Il concetto riveste un’ambiguità intrinseca giacché viene usato per riferirsi, talora partitamente ma a volte in modo congiunto, a molteplici referenti, quali: il grado di interdipendenza oggettivamente osservabile tra membri o componenti strutturali di una società; la varietà e variabilità dei mutamenti di stato di una società; la difficoltà che un attore-osservatore incontra volendo costruirsi un modello efficace, in vista di determinati scopi, di una data società, o per rendere una descrizione attendibile di parti di essa; la difficoltà che un centro di potere incontra nel governare una società. Può quindi accadere che una società sia giudicata complessa da un medesimo o da diversi attori sociali, perché possiede certe proprietà intrinseche di struttura o di funzionamento, oppure perché l’attore avverte dinanzi a essa i propri limiti cognitivi, o quelli del proprio potere; o anche per tutte queste ragioni insieme. Società c. è dunque una denominazione convenzionale (in contrapposizione a società semplici o primitive) delle società in cui lo sviluppo dell’insieme dei diversi settori della cultura (tecnologia, organizzazione politica e sociale, religione ecc.) abbia raggiunto una elevata c. globale; la denominazione si applica in genere alle società industrializzate, dotate di sistemi politici centralizzati, stratificazione sociale e diversificazione interna del lavoro. Si tratta evidentemente di una definizione di comodo, non potendosi stabilire un punto di discrimine universalmente valido tra società semplici e società c.: in taluni campi della cultura, anzi, quali l’organizzazione sociale e cerimoniale, le arti ecc., le società semplici presentano spesso una capacità di elaborazione maggiore delle società complesse.