frattale
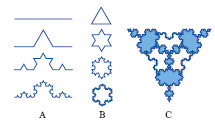
In matematica, termine coniato nel 1975 dal matematico francese B. Mandelbrot per indicare un particolare ente geometrico la cui forma è invariante nel cambiamento della scala delle lunghezze (proprietà di invarianza di scala): successivi ingrandimenti di piccole regioni dell’oggetto mostrano sempre la stessa struttura, spesso assai complessa. La forma del f. non si presenta quindi regolare come, per es., nelle figure elementari della geometria euclidea che a piccole scale perdono la loro struttura, bensì estremamente frastagliata. In fig. sono riportati esempi di procedimenti ricorsivi per la costruzione di un f.: un segmento viene diviso in tre parti uguali e la parte centrale è sostituita da due segmenti di lunghezza pari a quello eliminato; si genera così una figura con quattro segmenti, a ciascuno dei quali si applica lo stesso procedimento ottenendo le figure successive (fig. A) il f. è l’oggetto che si ottiene applicando questo processo all’infinito. Lo stesso processo è applicato contemporaneamente a tre segmenti uguali disposti secondo i lati di un triangolo equilatero (fig. B; curva di von Koch, nota anche come curva a fiocco di neve). Lo stesso procedimento è infine applicato a più segmenti diversamente disposti (fig. C).
Il grado di irregolarità e frammentazione di un f. può essere caratterizzato quantitativamente da un numero, detto dimensione f., non necessariamente intero. I f. hanno importanza nella descrizione delle forme naturali: sono f. le linee costiere, la forma delle nuvole, gli aggregati di particelle in sospensione nei liquidi, i polimeri ecc.; così come f. sono le caratteristiche di alcuni importanti fenomeni fisici, quali la turbolenza sviluppata (➔ turbolenza), il caos deterministico (➔ caos), i processi di cammini casuali ecc.
Il concetto di dimensione ha un ruolo centrale nella caratterizzazione dei frattali. Usualmente si definisce la dimensione di un oggetto come il numero di direzioni indipendenti accessibili a un punto che si muove su di esso. Tale dimensione viene detta dimensione topologica, DT, ed è un numero intero non negativo, inferiore o uguale alla dimensione dello spazio in cui l’oggetto è immerso. Questa dimensione non è però in grado di descrivere le caratteristiche geometriche di un generico oggetto. Per es., una curva regolare (per essere più precisi differenziabile) e la curva di Peano (continua ma non differenziabile, che riempie densamente un quadrato ➔ curva) hanno manifestamente proprietà assai differenti pur avendo la stessa dimensione topologica DT=1. È necessario perciò introdurre un indice che riesca a distinguere tra oggetti con la stessa dimensione topologica. Questo indice è la dimensione di ricoprimento o f., DF, definita considerando il numero di ipercubi di spigolo ε necessari a ricoprire l’oggetto, per ε→0. Tale numero, N(ε), al diminuire di ε aumenta come N(ε)∝ε−DF. Qualche volta DF viene chiamata dimensione di Hausdorff (quest’ultima ha una definizione più complessa e, in alcuni casi, può non coincidere con DF). Si deve sottolineare che DF può essere non intera e che per un oggetto geometrico regolare essa coincide con la dimensione topologica. I f. sono oggetti per i quali DF è maggiore della dimensione topologica: più una forma è frastagliata, tanto maggiore è la differenza tra la dimensione f. e quella topologica. La curva di Peano ha DF=2 e presenta un elevatissimo grado di frastagliamento, in quanto DF è uguale alla dimensione del piano in cui la curva è immersa.
I f. sono modelli delle forme naturali e non solo patologie dell’usuale geometria analitica. Si pensi alle linee costiere, la cui lunghezza aumenta al diminuire della lunghezza di risoluzione, e, dello strumento di misura. Per es., la costa inglese e quella greca, molto frastagliate, hanno DF≃1,3; mentre le piatte coste sudafricane hanno una DF molto prossima all’unità. Anche alcuni importanti fenomeni fisici sono descrivibili in termini di oggetti f.: nell’idealizzazione matematica (processo di Wiener) del moto browniano di una particella, causato dagli urti irregolari con le molecole del fluido in cui la particella è in sospensione, la traiettoria della particella è una curva continua ma non differenziabile in alcun punto, con DF=2. In un fluido incomprimibile tridimensionale, la turbolenza sviluppata presenta caratteristiche f. su scale di lunghezza sufficientemente piccole: l’energia dissipata è in gran misura concentrata su un f. con DF≃2,8.
La dimensione f. è una proprietà puramente geometrica e molte leggi di scala di osservabili fisiche su di un f. non possono essere caratterizzate completamente da quest’unico esponente. È questa la ragione per la quale si deve attribuire al f. una distribuzione di ‘massa’ dipendente dal fenomeno considerato; nella turbolenza, per es., la massa è l’energia dissipata. In generale la distribuzione di massa non è uniforme, ma il f. può essere ancora pensato come l’incastro di una famiglia di f., ognuno di essi con distribuzione uniforme, cui viene dato il nome di multifrattale. Il concetto di multifrattale si è rivelato assai utile nell’analisi di molti fenomeni complessi quali i processi di aggregazione, i sistemi dinamici caotici, i sistemi disordinati, la turbolenza sviluppata.