aberrazione

Astronomia

fig. 1

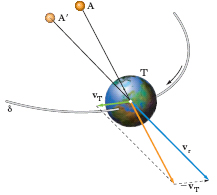
A. astronomica Fenomeno, scoperto da J. Bradley nel 1727, per cui, a causa dei moti della Terra, un astro appare sulla volta celeste in una posizione A’  leggermente diversa da quella A nella quale si vedrebbe se la Terra fosse priva di moto, nella direzione corrispondente al risultante v_r della velocità della luce proveniente dall’astro e dell’opposto della velocità v_T della Terra (fig. 1). L’a. dovuta al moto di rivoluzione annuo della Terra sulla sua orbita δ intorno al Sole è detta a. annua: essa dà luogo sulla volta celeste a un apparente movimento annuo degli astri, i quali nel corso di un anno descrivono su quella una piccola ellisse, il cui semiasse maggiore ha un’ampiezza angolare (identica per tutte le stelle) di 20,48″ ( costante di a.), tanto più schiacciata quanto più la stella è vicina all’eclittica. L’importanza del fenomeno sta nel fatto che dalla misurazione della costante di a. si può risalire, nota che sia la velocità della luce, alla distanza Terra-Sole, cioè all’unità astronomica.

Biologia

A. cromosomiche Alterazioni che insorgono nella struttura dei cromosomi spontaneamente oppure in seguito a trattamenti sperimentali (per es., raggi X, sostanze mutageniche). Sono classificate come duplicazioni, delezioni, traslocazioni, inversioni (➔ mutazione).

Fisica

fig. 2A

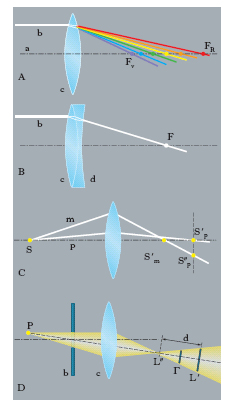
A. ottiche Un sistema ottico, sia esso rifrangente (sistema diottrico) o riflettente (sistema catottrico), presenta a. o è aberrante se le immagini che esso dà non sono geometricamente simili agli oggetti (sistema non ortoscopico) o non sono nitide (sistema non stigmatico) o variano d’aspetto al variare del colore della luce (sistema non acromatico). Le a. di un sistema ottico non derivano da imperfezioni delle superfici rifrangenti o riflettenti, ma dalla geometria del sistema e dai materiali. A. cromatica (o cromatismo) Fenomeno, che si verifica soltanto nei sistemi diottrici, quando l’immagine di una sorgente puntiforme policromatica posta sull’asse del sistema è formata da tante immagini quanti sono i colori di cui è composta la luce. Ciò avviene perché l’indice di rifrazione delle lenti del sistema, e quindi la distanza focale del sistema medesimo, varia con la frequenza cosicché i raggi emergenti convergono in punti dell’asse diversi a seconda della frequenza della luce (fig. 2A: la lente c fa convergere in F_V i raggi violetti e in F_R i raggi rossi del fascio di luce bianca b, parallelo all’asse ottico a). Un modo di ottenere un sistema esente da tale a. (acromatico) è quello di unire due lenti sottili scelte per forma e qualità di vetro in modo opportuno. Accoppiando, per es., un menisco convergente di vetro crown, c (fig. 2B), a un menisco divergente di vetro flint, d, si realizza un sistema (doppietto acromatico) il cui fuoco F è praticamente lo stesso per tutti i colori dello spettro. Con speciali tipi di vetro è possibile realizzare sistemi apocromatici per i quali la distanza focale è effettivamente la stessa per tutte le radiazioni visibili.

A. di sfericità (o sferica, o planatismo) A. di natura geometrica, dipendente cioè dalla forma delle superfici rifrangenti o riflettenti e dalla posizione, rispetto a esse, degli oggetti. Considerando una sorgente puntiforme monocromatica S sull’asse del sistema, se l’apertura angolare del sistema rispetto a S non è sufficientemente piccola, i raggi emergenti non concorrono più in un punto, ma inviluppano una superficie, la caustica, che è in ogni caso, per motivi di simmetria, superficie di rotazione intorno all’asse. Si distinguono un’a. sferica longitudinale, o assiale, a misura della quale si assume il segmento i cui estremi sono il punto S_p′ (fig. 2C), in cui converge il raggio parassiale p, e il punto S_m in cui converge il raggio marginale m, e un’a. sferica trasversale, misurata dal segmento i cui estremi sono l’anzidetto punto S_p′ e il punto S_p″, intersezione del raggio marginale m con il piano per S_p′ perpendicolare all’asse a del sistema. Un sistema esente da questa a., cioè un sistema aplanatico, si realizza unendo una lente convergente e una divergente: le a. di sfericità della prima lente sono annullate (perché di segno opposto) da quelle della seconda lente. Condizioni necessarie e sufficienti per conseguire tale risultato sono la condizione di Herschel (➔) per quanto riguarda l’a. sferica assiale, quella di Abbe (➔) per quanto riguarda l’a. sferica trasversale.

A. analoga alla precedente, ma riguardante punti oggetto non situati sull’asse del sistema. Se la sorgente puntiforme A non è sull’asse e il sistema è, rispetto alla sorgente, di notevole apertura, i raggi emergenti inviluppano ancora una caustica, che però non è più di rivoluzione attorno all’asse ottico. Su uno schermo piano, normale all’asse del sistema, si ottengono figure luminose che ricordano la forma delle comete, da cui deriva il nome.

aberrazione Astigmatismo e curvatura di campo Si riferiscono entrambe a punti oggetto fuori dell’asse e a un sistema di piccola apertura. Illuminando una lente c (fig. 2D) fortemente diaframmata (diaframma circolare b avente il centro sull’asse a) con raggi provenienti da un punto P fuori dell’asse e abbastanza lontano da esso, i raggi emergenti non danno più un’immagine stigmatica (cioè non concorrono più in un punto) e si distribuiscono in modo da appoggiarsi a due lineette stigmatiche, l’una, L′, giacente nel piano per l’asse e per P, detta sagittale; l’altra, L″, normale a questo piano, detta tangenziale. Le due lineette stigmatiche si dicono anche focali di Sturm o immagini astigmatiche del punto P. La loro distanza d misurata lungo il raggio principale (raggio per P e per il centro del diaframma) misura l’a. astigmatica. Tra le lineette viene a formarsi un cerchietto luminoso, detto di minima confusione, che costituisce anch’esso una pseudoimmagine di P. Nella zona in cui si formano le lineette stigmatiche si ha un graduale passaggio della sezione del fascio da ellittica a lineare, poi circolare, ancora lineare e ancora ellittica. Un sistema esente da astigmatismo si dice anastigmatico. Per quanto riguarda la curvatura di campo, essa consiste nel fatto che anche in un sistema anastigmatico a una figura piana ortogonale all’asse corrisponde un’immagine curva. Si chiamano sistemi planeici o planetici o anastigmatici a campo piano i sistemi corretti dalla duplice aberrazione dell’astigmatismo e della curvatura di campo; per sistemi del genere debbono essere soddisfatte le condizioni di Petzval (➔).

fig. 3A

aberrazione Distorsione Realizzato un sistema planeico, non è detto che questo risulti anche ortoscopico (o rettolineare), che cioè le immagini risultino simili agli oggetti; si ha cioè in generale una distorsione delle immagini. In tal caso l’immagine di un reticolato a maglie quadrate (fig. 3A) posto in un piano perpendicolare all’asse si presenta o come nella fig. 3B (distorsione a barilotto) oppure come nella fig. 3C (distorsione a cuscinetto).