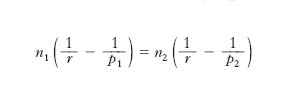parassiale
In ottica si dicono p., rispetto all’asse ottico di un sistema centrato, i raggi luminosi che, sia prima sia dopo la riflessione (o la rifrazione), formano con l’asse un angolo α molto piccolo.
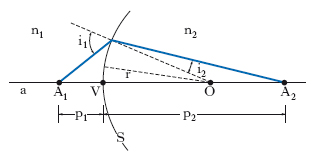
Invariante p. (v. fig.) In un diottro sferico siano n1, n2 gli indici di rifrazione dei due mezzi separati dalla superficie sferica S di centro O e raggio r; assumendo come verso positivo dell’asse ottico a quello che va dal mezzo 1 al mezzo 2, siano in valore e segno p1 e p2 rispettivamente le distanze dal vertice V di un punto A1 sull’asse e del suo coniugato A2 (in tal caso è sempre p1<0); inoltre r sia assunto positivo quando la superficie S volge la convessità verso il mezzo con indice di rifrazione n1. Si ha allora, per un raggio p., l’uguaglianza
,
equivalente alla legge di rifrazione n1seni1=n2seni2, dove i1 e i2 sono gli angoli rispettivamente d’incidenza e di rifrazione. Poiché la quantità nseni è, al variare di i, un invariante ottico, tale è anche, al variare di p, la quantità, che ha il nome di invariante p., n(1/r−1/p).