asintoto
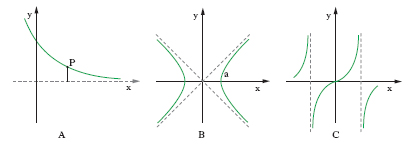
In geometria, retta a cui una curva si avvicina indefinitamente: precisamente una retta a si dice a. di una curva C, quando la distanza da a di un punto che percorra C e tenda ad allontanarsi indefinitamente ha per limite zero (senza tuttavia escludere che la curva e la retta possano avere punti comuni). Per es., un punto P (fig. A) che si muova sulla curva y=e−x si avvicina indefinitamente all’asse x quando la x tende a ∞: cioè l’asse x è a. per la curva y=e−x; altrettanto può dirsi per le curva x2−y2=a2 (fig. B) e y=tan x (fig. C). Per una curva algebrica un a. può anche definirsi come il limite della tangente alla curva quando il punto di contatto tende all’infinito: esso può quindi considerarsi come una retta tangente alla curva in un suo punto improprio (purché tale tangente sia distinta dalla retta impropria). Nella geometria proiettiva, infine, poiché non si fa più distinzione tra punti propri (al finito) e punti impropri (all’infinito), gli a. vengono trattati alla stessa stregua delle altre tangenti: in altri termini, cioè, la nozione di a. scompare.