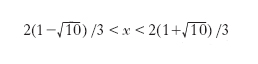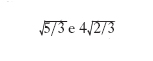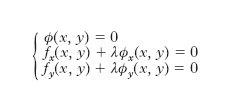massimi e minimi
Espressione con cui si indica l’argomento di molte ricerche matematiche, intese a individuare le massime e le minime grandezze tra un certo numero di grandezze assegnate, oppure i valori massimi e minimi assunti da una funzione o da un funzionale.
Generalità
Si definisce massimo (minimo) di un insieme ordinato A un elemento M (m) di A, tale che M ≥ a (m ≤ a) per ogni a ∈ A, come nel caso di m. di un insieme di numeri reali. Quale es. si pensi all’insieme dei numeri 1−x2 (essendo x un numero reale variabile): esso ammette come massimo il numero 1; invece l’insieme dei numeri 1−1/x2, pur ammettendo 1 come estremo superiore, non è dotato di massimo. Analogamente l’insieme dei numeri 1+x2 ammette come minimo il numero 1; invece l’insieme dei numeri 1+1/x2, pur ammettendo 1 come estremo inferiore, non è dotato di minimo.
M. di una funzione di una variabile reale Quando sia data una funzione f (x), reale di variabile reale, definita in un intervallo (a, b), essa può presentare massimi (minimi) relativi e massimi (minimi) assoluti; precisamente: se per un punto x0 dell’intervallo esiste un intorno contenuto nell’intervallo stesso, nei punti del quale la funzione assuma valori minori (maggiori) o tutt’al più uguali al valore assunto in x0, si dice che la funzione assume in x0 un massimo (minimo) relativo, e il valore di tale massimo (minimo) è f (x0); inoltre x0 si dice punto di massimo (minimo) o massimante (minimante) per la f (x). Per es., la funzione y=[4x2+(4/3)x3−x4]1/2 nell’intervallo
(fig. 1) ammette due massimi relativi nei punti di ascissa x=−1, x=2, ed essi valgono rispettivamente
Per massimo (minimo) assoluto della funzione f (x) nell’intervallo (a, b) si intende, quando esista, il massimo (minimo) dell’insieme dei valori assunti dalla funzione in tutti i punti dell’intervallo; esso coincide con il massimo (minimo) tra i massimi (minimi) relativi. Nell’es. precedente, il massimo assoluto
M.di una funzione di più variabili reali Nel caso delle funzioni di più variabili reali, le definizioni precedenti vanno modificate come segue. Sia f (P)=f(x1, x2, ..., xn) la funzione data, reale di n variabili reali, definita in un insieme A: si dice che essa ammette un massimo (minimo) relativo in un punto P0, appartenente ad A, se esiste un intorno I di P0 tale che nei punti P appartenenti a esso e ad A si abbia f (P) ≤ f (P0) (f (P) ≥ f (P0) ); il valore f (P0) è il massimo (minimo) relativo e P0 si chiama massimante (minimante) relativo. Per massimo (minimo) assoluto si intende, quando esista finito, il massimo (minimo) dei valori assunti dalla funzione in tutto A; esso risulta uguale al massimo (minimo) tra i massimi (minimi) relativi.
Criteri per l’esistenza di massimi e minimi
Ricordiamo anzitutto il classico teorema di Weierstrass: una funzione continua in un insieme chiuso e limitato di uno spazio euclideo a un numero qualunque di dimensioni vi ammette sempre almeno un massimo e almeno un minimo. Più generalmente, il teorema vale anche in relazione a un qualunque insieme compatto di uno spazio topologico. Torniamo ora a considerare funzioni definite in uno spazio euclideo, e fissiamo anzi l’attenzione su una funzione di due sole variabili f (x, y). Se P0(x0, y0) è un punto di massimo (minimo) per la f, allora la f (x0, y) ammette un massimo (minimo) per y=y0 e la f (x, y0) ha un massimo (minimo) per x=x0. Tuttavia non sempre vale il contrario; per es., la funzione f (x, y) della fig. 2 vale 1 nell’origine, è nulla sugli assi x, y e vale 2 fuori degli assi: essa non ha un massimo in O sebbene lo abbiano ciascuna delle funzioni f (x, 0) e f(0, y). Consideriamo, per ultimo, il caso di una funzione di più variabili reali che ammetta tutte le derivate parziali prime e seconde nell’intorno di un punto P0. In queste ipotesi, se in P0 vi è un massimo (minimo) della f (P), in P0 sono nulle tutte le derivate parziali prime e l’hessiano della f (P), calcolato in P0, risulta essere il determinante di una forma quadratica definita negativa (positiva); in particolare, per le funzioni di una variabile accade che la derivata prima è nulla e quella seconda è negativa (positiva); per le funzioni di due variabili accade che le due derivate parziali prime sono nulle, l’hessiano è < 0 (> 0) e le due derivate parziali seconde sono entrambe negative (positive). Per il massimo e il minimo limite di una variabile ordinata ➔ limite.
Ricerca di massimi e minimi
Il problema della ricerca dei m. fu trattato fin dall’epoca greca limitatamente però a questioni di aritmetica (massimo comune divisore, minimo comune multiplo) e di geometria piana (aree di parallelogrammi inscritti in un triangolo e aventi un lato sopra un lato del triangolo; distanza di un punto variabile sopra una conica da un punto fisso del piano; area di una figura piana di dato perimetro: è quest’ultimo il cosiddetto problema degli isoperimetri). Nel tardo Medioevo e nel Rinascimento (N. d'Oresme, Giordano Nemorario, Regiomontano, B. Cavalieri, E. Torricelli) si affrontano problemi di natura più generale, anche se talvolta più semplici (per es.: massimo di xy, o di xy2, o di xyn, nel caso che x+y si mantenga costante) e si cominciano a delineare vari metodi che più tardi, avendo come geniale precursore P. Fermat, si concretano nel metodo differenziale di I. Newton e G.W. Leibniz e sono in seguito perfezionati e resi rigorosi, principalmente a opera della critica del 19° sec. (K. Weierstrass, A.-L. Cauchy ecc.).
Nei tempi più recenti si sono studiati e si studiano metodi atti a trattare il problema in casi sempre più estesi (➔ variazione). Modernamente quando si parla di ricerca dei m. ci si riferisce per lo più ai m. di una grandezza variabile con continuità, quale può essere una funzione di più variabili, indipendenti oppure vincolate tra loro da certe relazioni (per es.: la funzione xy delle variabili reali x, y, legate dalla relazione x+y=c=costante positiva, ammette c2/4 come massimo, e lo raggiunge per x=y=c/2), oppure una funzione di linea o più generalmente un funzionale (per es.: tra i poligoni inscritti in una circonferenza e aventi un dato numero di lati, hanno area massima quelli regolari).
M. per le funzioni
Quando sia data una funzione w=f (x, y, ...), di un qualsivoglia numero di variabili, definita in un insieme A, si distingue anzitutto il caso dei m. liberi dal caso dei m. vincolati; nel primo caso si cercano i m., assoluti o relativi, della w, quando le variabili indipendenti x, y, ... variano liberamente nell’insieme di definizione; nel secondo caso si cercano i m., assoluti o relativi, della w, quando le variabili x, y, ... siano legate da una o più relazioni.
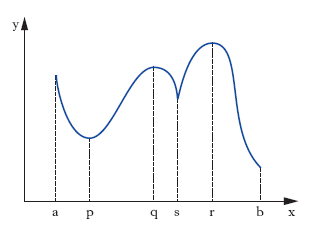
M. liberi per le funzioni di una variabile. - Limitiamoci per semplicità al caso di una funzione y=f (x), definita nell’intervallo chiuso [a, b] dell’asse x. In base ai teoremi sui m., i valori di x nei quali la funzione assume i suoi eventuali m. relativi o assoluti (valori estremanti) sono da ricercarsi tra le seguenti tre categorie di valori: a) i valori di x, interni all’intervallo, nei quali si annulla la derivata prima della funzione (p, q e r in fig. 3: valori estremali); b) gli estremi a e b dell’intervallo; c) i valori di x interni all’intervallo, per i quali non esiste la derivata prima (punto s). Precisamente: se per un valore ξ della categoria I si ha f″ (ξ) > 0, o f″ (ξ) < 0, ξ è un valore rispettivamente minimante o massimante, e quindi f (ξ) è un minimo o un massimo (relativo). Se f′ (ξ)=f″(ξ)=...=fn (ξ)=0 ed fn+1 (ξ)≠0, per n dispari la f (ξ) ammette in ξ un minimo o un massimo secondo che fn+1 (ξ) < 0, o fn+1(ξ) > 0, per n pari invece la f (ξ) ha in ξ un punto di flesso ordinario. Se in ξ la funzione non ammettesse derivata seconda, esso andrebbe studiato come quelli della terza categoria; analogamente dicasi per le derivate successive. Se per l’estremo sinistro a dell’intervallo si ha f′ (a) > 0 [o f′ (a) < 0], la funzione presenta ivi un minimo [o un massimo]; se f′ (a) = 0 e f″ (a) > 0 [o f″ (a) < 0], si ha rispettiva;mente un minimo [o un massimo]; ecc. Se per l’estremo destro b si ha f′ (b) < 0 [o f′ (b) > 0], oppure f′ (b)=0 e f″ (b) > 0 [o f″ (b) < 0], oppure: f′ (b)=f″ (b)=0 e f‴ (b) < 0 [o f‴ (b) > 0] ecc., si ha ivi un minimo o rispettivamente un massimo. Per i punti della terza categoria non esistono regole generali per riconoscere eventuali estremanti: si ricorre allora, per solito, all’esame diretto dei valori assunti dalla funzione in ciascuno di essi.
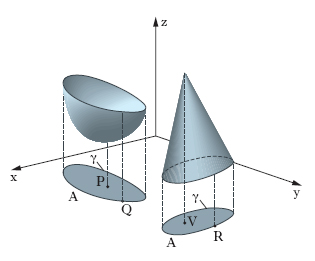
M. liberi per le funzioni di due o più variabili. - Ci limitiamo per semplicità al caso di una funzione w=f (x, y) di due variabili, definita in un dominio limitato A che ha per contorno una linea regolare γ. Le coppie di valori (ξ, η) che corrispondono a m. relativi per la w, cioè, come si dice, i punti estremanti, vanno ricercate tra le seguenti tre categorie di punti: a) punti interni ad A nei quali si annullano le due derivate parziali prime fx (x, y) e fy (x, y) della funzione (punti estremali, P in fig. 4); b) punti di γ (punti Q e R); c) punti interni ad A nei quali non esiste una almeno delle due derivate parziali prime (punto V ). Un punto (ξ, η) della prima categoria è un punto estremante se in esso è positivo il determinante hessiano della funzione, cioè l’espressione fxxfyy−f2xy (se tali derivate non esistessero o se l’hessiano fosse zero, il punto andrebbe esaminato come quelli della terza categoria): esso è precisamente un punto massimante o minimante a seconda che fxx (ξ, η) ha valore negativo o positivo. Se invece l’hessiano è negativo il punto (ξ, η) non è estremante. Per riconoscere la natura dei punti del contorno γ, occorrono considerazioni analoghe a quelle relative ai m. vincolati che permettano di distinguere su γ alcuni punti tra i quali vanno ricercati gli eventuali punti estremanti. Su questi punti così trovati, come pure sui punti della terza categoria, occorrerà, il più delle volte, operare con metodi diretti.
M. vincolati per le funzioni di due variabili. - Consideriamo una funzione w=f (x, y), definita in un dominio A del piano xy, nel cui interno è assegnata una porzione c di curva regolare, di equazione ϕ (x, y)=0; tale espressione rappresenta appunto il vincolo. Prescindiamo dai punti nei quali le funzioni f e ϕ non sono derivabili parzialmente e dagli estremi dell’arco c, punti che, al solito, occorre considerare a parte. Sia P (fig. 5) un punto di c che risulti di massimo (o di minimo) vincolato per la funzione f (x, y). Allora in P la curva c deve risultare tangente a quella curva di livello della funzione f che appunto passa per P. Ciò equivale a dire che in tale punto le derivate prime fx, fy risultano proporzionali alle ϕx, ϕy, oppure che il sistema nelle tre incognite x, y, λ (ove λ è una incognita ausiliaria, detta moltiplicatore):
[1] formula
ha una soluzione che è data dalle coordinate del punto P e da un opportuno valore di λ. Dunque, gli eventuali punti di m. vincolati vanno cercati tra le soluzioni del sistema [1]; tale procedimento è detto metodo dei moltiplicatori di Lagrange.
M. vincolati per le funzioni di più di due variabili.- Sia w=f (x1, x2,..., xn) la funzione data, siano ϕ1 (x1, x2,..., xn)=0, ϕ2 (x1, x2, ..., xn)=0,..., ϕs (x1, x2,..., xn)=0 gli s vincoli (s < n) ai quali si sottopongono le sue variabili indipendenti. Si chiedono i m. della w sulla varietà C definita dalle equazioni vincolari nell’insieme di definizione A della w. Trascurando i punti nei quali si presentano fenomeni di singolarità, il metodo dei moltiplicatori di Lagrange fornisce le seguenti condizioni necessarie perché un punto sia punto di massimo o di minimo vincolato:
esso è un sistema di n+s equazioni nelle n+s incognite x1, x2, ..., xn; λ1, λ2, ..., λs. Le λ1, λ2, ..., λs sono appunto i moltiplicatori. È da notare che in molti casi il metodo dei moltiplicatori, anche se non fornisce con facilità i punti estremanti o gli estremi, dà tuttavia rapidamente le condizioni alle quali devono soddisfare gli enti considerati per realizzare il massimo o il minimo.