suono

La sensazione uditiva e le vibrazioni di un mezzo (per lo più l’aria, ma anche mezzi elastici qualunque) che possono produrre tale sensazione. Per estensione, tutte le vibrazioni propagantisi in un mezzo, anche se non udibili per frequenza o intensità. Le vibrazioni possono essere eccitate nel mezzo o a esso trasmesse dalle vibrazioni di un corpo (sorgente sonora) e a loro volta eccitano l’orecchio (generalmente per azione diretta sul timpano).

Fisica

Cenni storici

Le prime ricerche sistematiche sui s., cioè le prime ricerche di acustica, risalgono, nell’antichità classica, a Pitagora e alla sua scuola, cui particolarmente sono dovuti studi sui s. emessi da tubi sonori e corde vibranti. È di Vitruvio la scoperta di una certa analogia fra il meccanismo di propagazione del s. e il movimento delle onde su uno specchio d’acqua; mentre è attribuibile a Plinio il Vecchio la constatazione che il s. si propaga con velocità molto minore della luce e a Tolomeo l’idea che l’altezza d’un s. dipenda in definitiva da proprietà meccaniche della sorgente sonora.

Uno studio sperimentale sistematico dei fenomeni sonori ha inizio con G. Galilei, cui risalgono idee e ricerche sulla natura del s. e sui suoi caratteri, sulle proprietà delle corde vibranti, sui metodi per la determinazione della velocità del s. nell’aria ecc.; a lui è dovuto in particolare l’aver riconosciuto nell’altezza d’un s. un elemento legato alla frequenza di vibrazione della sorgente sonora e di aver intuito la natura composita del s. delle corde. Quasi contemporanee all’opera di Galilei sono quelle di G. Benedetti, di G.F. Sagredo, che nel 1615 dimostra che il mezzo di trasmissione del s. è l’aria, di M. Mersenne, che effettua una prima determinazione della velocità del s., e di P. Gassendi, cui è dovuta, fra l’altro, l’osservazione dell’indipendenza della velocità dall’altezza del suono. Nel 1663 O. von Guericke dimostra che il s. si propaga non solo nell’aria ma anche nei liquidi e nei solidi; frattanto, mentre si moltiplicano le misurazioni della velocità del s. nell’aria e si precisa l’influenza su di essa di vari fattori (vento, temperatura ecc.), alcuni problemi passano dall’ambito della sperimentazione a quello della ricerca teorica. Sono fra questi i problemi delle corde vibranti studiati da B. Taylor, da G. e D. Bernoulli, da L. Euler e soprattutto da d’Alembert. Nel 1710 J. Sauveur scopre il fenomeno dei battimenti; nel 1714 G. Tartini quello dei cosiddetti s. di combinazione; nel 1762 G.L. Lagrange dà, quasi contemporaneamente a D. Bernoulli, la teoria dei tubi sonori; nel 1786 G. Riccati illustra le leggi che regolano le vibrazioni delle membrane e delle verghe.

Le ricerche del 19° sec. approfondiscono, soprattutto a opera di H. von Helmholtz e lord Rayleigh, lo studio della propagazione ondosa e, in particolare, degli aspetti energetici di questa, mentre l’invenzione del fonografo e del microfono (1877) pone per la prima volta il problema della registrazione e della riproduzione dei s., nonché della loro trasduzione elettrica, problema che costituisce l’oggetto principale dell’elettroacustica. In quest’ultimo settore, crescendo l’importanza delle informazioni sonore nel quadro dei moderni mass media, e nel collegato settore dell’acustica architettonica (➔ acustica), si sono avuti i maggiori sviluppi.

Onde sonore e loro caratteristiche fisiche

Definizione

Il s. consiste in onde elastiche di appropriate caratteristiche, che, eccitate generalmente nell’aria da corpi elastici in vibrazione, si trasmettono agli organi sensibili dell’orecchio per il tramite dell’aria medesima (trasmissione aerea) o, eccezionalmente, attraverso la struttura ossea del cranio (trasmissione ossea). Si tende a considerare come onde sonore (eventualmente come ultrasonore al di sopra dei 20 kHz) tutte le onde elastiche di qualunque tipo ovunque propagantisi; in tal modo onda sonora coincide con onda elastica. Per le onde sonore si distinguono come caratteristiche intensità e frequenza. Relativamente alle onde udibili in aria, per quanto riguarda l’intensità, occorre che essa sia non minore di una soglia di udibilità, al di sotto della quale manca ogni sensazione, e non maggiore di una soglia di dolore, superata la quale la sensazione da acustica diventa dolorosa; per quanto riguarda la frequenza, occorre che essa sia compresa in un determinato intervallo, i cui limiti variano al variare dell’intensità (del resto, l’intervallo di intensità fra le due soglie anzidette varia al variare della frequenza); tale non semplice situazione è ulteriormente complicata dalla circostanza che soglie e limiti di frequenza variano da ascoltatore ad ascoltatore, com’è ben naturale per un fenomeno basato su sensazioni.

Per oggettivizzare quanto più il fenomeno, ci si suole riferire al cosiddetto orecchio normale, un orecchio fittizio (realizzabile con un microfono associato a opportuni filtri acustici ed elettrici) dalle caratteristiche del quale in effetti le caratteristiche dell’orecchio di una persona in buona salute e in età né troppo giovane né troppo avanzata non differiscono molto; il campo normale di udibilità, cioè gli intervalli di intensità e di frequenza di onde elastiche longitudinali nell’aria capaci di dar luogo a sensazioni acustiche nell’orecchio normale, resta poi convenzionalmente definito dall’audiogramma normale (➔ audiometria). Il campo normale di frequenza va da 16 a 20.000 Hz; si hanno infrasuoni al disotto di 16 Hz, ultrasuoni al disopra di 20.000 Hz.

Propagazione del suono

L’emissione di s. da parte di un corpo in vibrazione costituente la sorgente sonora e la loro propagazione sino all’orecchio di un ascoltatore, o, eventualmente, sino al microfono di un dispositivo di registrazione o di amplificazione sonora, avvengono secondo le leggi che governano la generazione e la propagazione di onde elastiche in genere. Per effetto del moto vibratorio della sorgente (per es., una corda o una membrana elastica in vibrazione, o anche una massa d’aria in oscillazione entro un recipiente aperto) si determina nell’aria circostante una successione di strati compressi e rarefatti, che si va allargando tutt’intorno (sono queste le onde longitudinali prima nominate): ciascuna delle particelle d’aria contigua alla sorgente prende a vibrare in sincronismo con questa, spostandosi al di qua e al di là della sua normale posizione d’equilibrio e trasmettendo il moto alle particelle a essa contigue lungo la retta che le congiunge con la sorgente (supposta, per semplicità, puntiforme), cioè lungo una direzione di propagazione, o raggio sonoro, dei s. emessi dalla sorgente.

A caratterizzare la perturbazione, punto per punto e istante per istante, può essere assunto lo spostamento s che la generica particella d’aria subisce; se s è una funzione sinusoidale del tempo t, si parla di s. puro, altrimenti si parla di s. composto (o non puro); in questo caso il s. si può pensare costituito dalla sovrapposizione di s. armonici, cioè di s. puri di opportuna ampiezza e fase iniziale e di frequenza multipla di quella del s. armonico di frequenza più bassa, detto primo armonico o, più correntemente, s. fondamentale; le caratteristiche dei s. armonici costituenti un s. composto si ottengono mettendo in opera i metodi dell’analisi armonica (➔ armonico). Considerando dunque un s. puro, lo spostamento s delle particelle d’aria a distanza d dalla sorgente può essere descritto mediante la relazione:

[1]

formula,

dove a è l’ampiezza d’oscillazione, ω la pulsazione, pari a 2π volte la frequenza f o pari a 2π/T, con T=1/f periodo del s., e v è la velocità di propagazione della perturbazione sonora. Quest’ultima risulta pari a

,

dove ρ è la massa specifica e c il coefficiente di compressibilità dell’aria, o genericamente del mezzo elastico in cui si propagano le onde sonore. Per un fluido si distingue fra compressibilità adiabatica e compressibilità isotermica; la frequenza delle onde sonore (16-20.000 Hz) è sufficientemente grande perché le rapide compressioni e rarefazioni che le onde provocano nel fluido si possano considerare adiabatiche, sicché a c si può lecitamente assegnare il valore adiabatico. Nel caso dell’aria secca a pressione e temperatura normali è lecita anche l’approssimazione dei gas perfetti, per cui è c=(γp0)−1, con γ rapporto fra il calore specifico a pressione p0 costante e quello a volume costante; così, si ha:

[3]

formula.

Sostituendo ai simboli delle varie grandezze gli appropriati valori numerici, si trova v=331 m/s, in ottimo accordo con il valore che l’esperienza dà per l’aria secca a 1 bar e a 0 °C.

Come risulta dalla [3], nell’aria secca, e, in genere, in un mezzo omogeneo, la velocità di propagazione del s. non dipende dalla frequenza del s. medesimo: come si usa dire, nella propagazione non vi è dispersione. Accade però che, in mezzi particolari, s. di frequenza diversa possano propagarsi con velocità diversa; ciò ha rilevanza non tanto per i s. puri, quanto per quelli composti, poiché i diversi s. armonici componenti, che dapprima procedono tutti raggruppati, finiscono con il separarsi più o meno notevolmente: ciò porta a distinguere la velocità dei singoli s. armonici, che viene detta velocità di fase di ognuno di essi, dalla velocità con cui procede il s. composto, detta velocità di gruppo, che è anche la velocità con cui si propaga l’energia associata al s. in questione. In un mezzo non dispersivo, in cui cioè la velocità (di fase) non dipende dalla frequenza, le due velocità ricordate coincidono, e coincidono anche in un mezzo dispersivo se il s. è un s. puro. Naturalmente, l’una e l’altra di queste velocità sono ben diverse dalla velocità con cui le particelle sollecitate dall’onda sonora descrivono il loro moto vibratorio:

La relazione ora scritta rappresenta l’onda di velocità, che ha ampiezza aω ed è sfasata di π/2 rad in anticipo rispetto all’onda di spostamento rappresentata dalla [1]; sia la [4] sia la [1] sono rappresentazioni equivalenti della perturbazione sonora.

Un’altra, ed espressiva, rappresentazione della perturbazione sonora è possibile introducendo la pressione sonora, o ampiezza di pressione, che è la differenza Δp fra la pressione p istantanea e la pressione p0 media del fluido (p0 è la pressione che regna nel fluido in assenza di onde); è:

Così, l’onda di pressione ha ampiezza aω/(cv), è in fase con l’onda di velocità e in quadratura in anticipo con l’onda di spostamento. Δp non va confusa con la pressione del s., che è la pressione esercitata dall’onda sonora contro un ostacolo su cui venga a incidere e che ha carattere continuo nel tempo (pressione di radiazione sonora). Genericamente parlando, si può dire che tale pressione è proporzionale al valore medio dell’energia totale associata all’onda sonora; di questa energia sonora è misura l’intensità (energetica) I, definita appunto come l’energia che, seguendo l’onda, fluisce nell’unità di tempo attraverso una superficie di area unitaria, ortogonale alla direzione di propagazione dell’onda:

dove il pedice eff indica che si tratta di un valore efficace (radice quadrata del valore quadratico medio); nel caso di s. puri, è: I=(ρv)(aω)2/2.

Le relazioni ora scritte ricordano quelle che danno la potenza elettrica in un circuito resistivo, ove si faccia corrispondere la pressione sonora alla forza elettromotrice, lo spostamento (o la portata acustica) alla carica elettrica, la velocità all’intensità di corrente e la quantità ρv, perciò detta resistenza acustica (areica) o anche, più in generale e correttamente, impedenza caratteristica del mezzo, alla resistenza o impedenza elettrica; è questo uno dei fatti su cui si basa l’analogia elettroacustica, che, consentendo di trattare dispositivi sonori mediante il ricorso a modelli elettrici, facilita grandemente la risoluzione di molti problemi di acustica applicata. Di evidente derivazione elettrica in questo quadro analogico è poi l’uso del decibel, anziché del fon, per esprimere intensità o meglio livelli di intensità di sensazioni sonore così come intensità o meglio livelli di intensità energetiche; in quest’ultimo caso, la misura l in decibel (decibel acustici) di un’intensità I o meglio del livello sonoro corrispondente all’intensità I, si ottiene mediante la relazione l=10 Log(I/I0), dove I0 è un’intensità di riferimento, assunta pari a 10−12 W/m2 (corrispondente alla soglia di udibilità in aria alla frequenza di 1000 Hz); alternativamente, a norma delle [6], si ha anche l=20 Log(Δpeff/Δpeff0), dove Δpeff0 è la pressione sonora efficace corrispondente all’intensità I0: per I0=10−12 W/m2, si ha Δpeff0=2∙10−5 Pa.

Come già detto, la propagazione dei s. è governata dalle leggi riguardanti la propagazione delle onde elastiche in genere. Così, in un campo sonoro indefinito, cioè in un mezzo omogeneo illimitato, la propagazione è per raggi rettilinei; lungo uno di tali raggi l’intensità normalmente decresce al crescere della distanza percorsa d, sia perché l’energia sonora si ripartisce su fronti d’onda progressivamente più estesi (nel caso di onde sferiche, tale attenuazione geometrica varia con il quadrato di d) sia perché l’energia dell’onda è assorbita dal mezzo e ivi dissipata in calore (tale attenuazione per assorbimento è regolata dalla legge di Bouguer-Lambert e varia quindi esponenzialmente con d: ➔ assorbimento); variazioni d’intensità, peraltro senza dissipazione di energia, possono essere causate anche da fenomeni di interferenza con altre onde, mentre variazioni apparenti di frequenza possono aversi, per effetto Doppler, se la sorgente sonora è in moto.

Assai più complicata è la situazione se il mezzo non è illimitato e omogeneo, in quanto allora normalmente si verificano fenomeni di riflessione e di rifrazione su e attraverso zone di discontinuità, di diffusione su superfici di discontinuità a piccola scala, di diffrazione su ostacoli, oltre ai già nominati fenomeni di interferenza, i quali tutti concorrono ad alterare la forma dei raggi sonori, che in genere non è più rettilinea indefinita, e l’intensità dei suoni. Questi fenomeni si presentano con le stesse, ben note modalità con cui si manifestano per la luce; in perfetta analogia con quanto si fa nell’ottica, anche per i s. è comodo distinguere tra fenomeni di acustica geometrica e fenomeni di acustica fisica, collocando fra i primi quelli nei quali è irrilevante la natura ondulatoria della perturbazione e che quindi possono essere descritti in termini di soli raggi sonori. Circa i fenomeni di diffrazione, è da osservare che essi sono molto evidenti in acustica; infatti, la lunghezza delle onde sonore, λ=v/f, è, nell’aria, compresa all’incirca fra 2 cm per le frequenze più alte, e 20 m per le frequenze più basse, e ha quindi valori non solo confrontabili ma in moltissimi casi addirittura maggiori delle dimensioni degli ostacoli: è in virtù di questo fatto che, come mostra l’esperienza quotidiana, non è facile ‘ripararsi’ da s. non graditi mediante schermi che ‘facciano ombra’, i quali sono assai spesso aggirati, per diffrazione, dai s. medesimi.

Riguardo all’assorbimento, è da ricordare che nell’aria, e nei fluidi in genere, esso avviene principalmente a causa della resistenza viscosa offerta dal mezzo e del riscaldamento che si ha nelle zone compresse dall’onda. Il coefficiente lineare di assorbimento per viscosità, αv, vale 8π2ηf2/(3ρv3), dove η è la viscosità, mentre quello di assorbimento termico, αt, vale 2π2f2kTβ2/(ρvcp2), dove k è il coefficiente di conducibilità termica, T la temperatura, β il coefficiente di dilatazione termica, cp il calore specifico a pressione costante; per gli aeriformi αt è circa un terzo di αv, mentre è praticamente trascurabile per quasi tutti i liquidi. In realtà, i valori dedotti sperimentalmente per il coefficiente globale di assorbimento sono notevolmente maggiori di quelli dedotti dalle precedenti formule; questo dipende dal fatto che sono da prendere in considerazione anche interazioni a livello molecolare.

Benché, come più volte precisato, per onde sonore debbano propriamente considerarsi quelle propagantisi nell’aria o in altro fluido in cui si possa trovare un ascoltatore, si finisce con il prendere in considerazione anche la propagazione in mezzi elastici qualunque, compresi quelli solidi: ciò sia perché molto spesso il s. emesso da una sorgente può pervenire all’orecchio attraverso una serie di mezzi diversi, sia perché in varie applicazioni tecniche il ricevitore acustico può trovarsi in ambiente diverso dall’atmosfera. Per gli aeriformi, la velocità di propagazione v è praticamente data dalla [3] ed è dell’ordine, in condizioni standard, di qualche centinaio di metri al secondo; per i liquidi, si ha v=(ρc)−1/2 ed è dell’ordine del migliaio di metri al secondo, mentre per i solidi è v=(E/ρ)1/2, con E modulo di Young, ed è dell’ordine di qualche migliaio di metri al secondo. La resistenza acustica interviene in maniera essenziale a determinare la propagazione attraverso la superficie di separazione fra due mezzi diversi; infatti, posto r21=R2/R1, dove R1, R2 sono le resistenze acustiche dei due mezzi a contatto, il coefficiente di riflessione, cioè il rapporto fra l’energia riflessa dalla superficie di separazione e l’energia incidente, per incidenza normale vale (r21−1)2/(r21+1)2: così, se R2≫R1, come accade quando s. propagantisi nell’aria incidono su materiali solidi, o anche su superfici liquide, il coefficiente anzidetto vale praticamente 1, cioè tutta l’energia incidente viene riflessa. Ciò è rigorosamente vero solo se i due mezzi al di qua e al di là della superficie di separazione sono illimitati; se, come spesso accade, il mezzo su cui i s. incidono è limitato, cioè stratiforme, esso si comporta come una membrana spessa e, entrando in vibrazione, trasmette energia sonora ad altri mezzi successivi.

Caratteri distintivi dei suoni

Sono, con tradizionale riferimento alla qualità delle sensazioni acustiche, l’altezza, l’intensità e il timbro (o colore, o metallo).

fig. 1

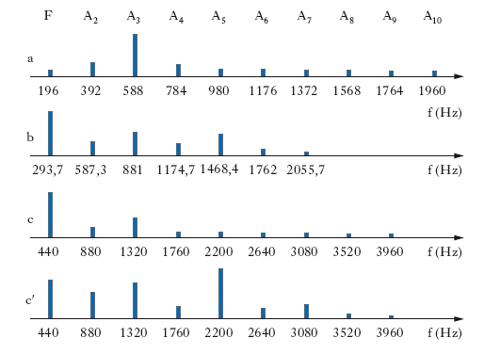
Per quanto riguarda l’altezza, essa è legata alla frequenza delle onde sonore; precisamente, un s. si dice tanto più alto, o acuto, e tanto meno basso, o grave, quanto maggiore è la sua frequenza se si tratta di un s. puro o quanto maggiore è la frequenza del s. fondamentale se si tratta di un s. composto. Relativamente a quest’ultimo caso, è importante il fatto che l’altezza è sempre fisiologicamente determinata dalla frequenza del s. fondamentale, anche se questo ha intensità assai minore di quella di successivi armonici: indicativo al riguardo è l’esempio di fig. 1, dove è riportato lo spettro di alcune note di violino: nel primo caso, a determinare l’altezza corrispondente alla nota musicale di cui si tratta è il debole s. fondamentale a 196 Hz.

Quanto all’intensità, qui si tratta dell’intensità della sensazione sonora, in base alla quale i s. sono distinti, soggettivamente, in forti, o intensi, e deboli. Il collegamento, convenzionale, fra questa grandezza, ovviamente di carattere non fisico, e l’intensità energetica è costituito, come sopra accennato, dall’audiogramma normale: ricorderemo che unità di misura, logaritmica, è il fon. La misurazione di questo carattere, importante, per es., in audiometria, si basa sul fatto che a 1000 Hz la misura in fon uguaglia quella del livello sonoro in decibel; si fanno giungere all’orecchio, alternativamente, il s. in esame e il s. a 1000 Hz di un generatore, variando il livello di quest’ultimo sinché l’orecchio giudica i due s. ugualmente forti: il livello sonoro, in dB, del s. a 1000 Hz misura l’intensità, in fon, dell’altro suono. È così possibile, in particolare, tracciare le curve di uguale intensità di sensazione sonora (isofone) costituenti l’audiogramma dell’orecchio in esame.

Relativamente, infine, al timbro, si tratta di un carattere, difficilmente precisabile in termini generali, che è legato alla composizione armonica dei s. (fig. 1): un s. puro è assolutamente privo di timbro, e perciò in genere non riesce gradevole quanto un s. dal ricco contenuto di armonici. Ciò che distingue una stessa nota musicale emessa da due strumenti diversi è appunto il diverso timbro: metallico, ligneo, sonoro, risonante ecc.

Psicoacustica

La psicoacustica è la disciplina che studia il complesso processo per cui un s. fisico diventa una percezione sonora. Lo studio di questo processo ha un carattere altamente multidisciplinare in quanto coinvolge l’acustica, l’elettromeccanica, la neurologia, la psicologia ecc. Molti risultati di acustica percettiva ottenuti nel campo della caratterizzazione delle capacità di analisi in tempo-frequenza dell’orecchio sono impiegati nelle moderne tecniche di compressione dei segnali sonori. Infatti, i più affermati sistemi di codifica del s. sfruttano i principali fenomeni di psicoacustica al fine di minimizzare e ottimizzare il numero di bit necessario per rappresentare un segnale sonoro. Tra i concetti più utilizzati figurano: a) la soglia di percezione uditiva assoluta, ossia la quantità di energia di un s. puro necessaria affinché un ascoltatore possa percepire il s. in un ambiente senza rumore; spesso il sistema di codifica fissa il punto più basso della curva della soglia in funzione della frequenza (all’incirca intorno ai 4 kHz) uguagliandolo all’energia rappresentata da un aumento o diminuzione di 1 bit del segnale; b) le bande critiche di frequenza, ossia le larghezze di banda per le quali il responso soggettivo cambia in modo sensibile, fenomeno collegato alla selettività che ha l’orecchio alle frequenze sonore, principalmente determinata dalla relazione tra frequenze percepite e posizione lungo la membrana basilare; c) il mascheramento, ossia il fenomeno per cui un s. non viene percepito a causa della presenza contemporanea di un altro s. più intenso: la spiegazione del meccanismo responsabile di questo effetto molto complesso, che dipende da vari parametri (come per es., la durata temporale del segnale) e si manifesta come mascheramento all’interno di una banda critica oppure, anche, di bande critiche vicine, può essere ricercata nell’inibizione, a livello della membrana basilare, causata dal s. forte, della trasmissione dell’oscillazione associata al s. debole. Sulla possibilità di quantificare il fenomeno del mascheramento si basano tutti i codici di compressione moderni, come, per es., il diffusissimo MP3. Infatti una grossa riduzione del numero di bit necessari per la codifica si ottiene allocando dinamicamente un numero di bit variabile in modo tale da perdere le componenti del segnale che si trovino sotto la soglia di mascheramento (e che quindi viene assunta come il livello del rumore di quantizzazione).

Fenomeni non lineari

Alcuni fenomeni (onde d’urto, generazione di armoniche, flusso di materia, cavitazione ecc.) che possono manifestarsi nella propagazione del s. (o più in generale di un’onda elastica) non sono descritti dall’equazione lineare delle onde (∂2ϕ/∂t2=v2∇2ϕ, dove ϕ è una qualsiasi grandezza fisica propria della propagazione, v una costante che rappresenta la velocità di propagazione dell’onda, ∇2 l’operatore laplaciano) che va sostituita da una forma non lineare nell’ambito della cosiddetta acustica non lineare. Il limite tra fenomeni acustici lineari e non lineari ovviamente non è netto: gli effetti di non linearità sono rilevanti quando il rapporto tra l’ampiezza della velocità di oscillazione delle particelle del mezzo e la velocità di propagazione dell’onda (cioè il numero di Mach, o, in modo del tutto equivalente, il rapporto tra la variazione della pressione dovuta all’onda e la pressione del mezzo a riposo o quello tra l’ampiezza della vibrazione e la lunghezza d’onda) non è molto minore dell’unità. Si può facilmente intuire l’origine di alcuni dei fenomeni non lineari, se si pensa, per es., a una corda vibrante tesa tra i due estremi fissi: se la corda descrive oscillazioni ampie, la sua lunghezza media nel tempo è apprezzabilmente maggiore di quando è a riposo, pertanto sarà maggiore la tensione media cui è sottoposta e quindi maggiore la velocità di propagazione dell’onda che la percorre; analogamente in un fluido investito da un’onda elastica sufficientemente intensa la pressione media è apprezzabilmente maggiore di quella che si avrebbe in assenza del suono. Il flusso di materia in fluidi sottoposti a intenso irraggiamento acustico si deve all’insorgere di una forza netta diversa da zero su ogni particella di fluido attribuibile alla media temporale di termini non lineari nell’equazione del moto. Si può inoltre avere cavitazione acustica o sonora (continua o impulsiva), cioè la formazione di cavità piene di vapore all’interno di un liquido prodotte dalle rapide variazioni locali di pressione associate all’onda acustica.

Primo, secondo, terzo, quarto suono; suono zero

Particolari processi di propagazione di onde sonore o, più spesso, ultrasonore hanno luogo in alcune sostanze liquide e in particolare nell’elio liquido. Precisamente, nell’elio liquido a temperatura minore di 2,17 K si parla di primo s. per indicare la propagazione ordinaria di onde acustiche o ultracustiche, che si ha se il fluido è omotermo e avviene in fase per le due componenti normale e superfluida (➔ superfluidità). Quando invece tali componenti non si propagano in fase, si parla di secondo s.; un modo per ottenerlo è disporre nell’elio un filo metallico percorso da corrente alternata e determinante quindi la propagazione di un’onda di temperatura: le due componenti si separano in quanto quella superfluida s’addensa nelle zone a temperatura maggiore. Nel caso che si abbiano onde elastiche superficiali, queste danno luogo al cosiddetto terzo s., mentre si parla di quarto s. con riferimento alla propagazione entro un capillare. S. zero è locuzione introdotta da L.D. Landau per indicare il modo di propagazione che si ha in 23He ad altissima frequenza e per temperature minori di 2,7 mK.

Musica

Il s. costituisce l’elemento sul quale si esercita l’azione di organizzazione strutturale della musica sul piano acustico (campo delle frequenze usato, criteri di determinazione del valore degli intervalli ecc.) e compositivo. A entrambi i piani non è indifferente la concezione del s., che lungi dall’essere determinata da pure considerazioni di ordine tecnico-scientifico, si configura come elemento di una generale visione antropologica. Non è un caso, per es., che la tradizione musicale colta d’Occidente – a differenza della tradizione popolare e di altre civiltà extraeuropee – abbia utilizzato soltanto gruppi di s. con frequenze che stanno tra loro in determinati rapporti, ponendo a livello ideologico una rigida distinzione tra s. (come prodotto di vibrazioni periodiche e regolari) e rumore, distinzione che le concrete esperienze compositive ed esecutive hanno costantemente smentito. In tempi recenti lo sviluppo delle tecniche di registrazione e di analisi connesse con le prassi compositive elettroniche, insieme con l’approfondimento delle tematiche legate alla percezione e alla psicologia dell’ascolto, hanno fatto registrare alcuni mutamenti nella concezione del s. nella musica occidentale. Nello stesso tempo le qualità tradizionalmente considerate come fondamentali del s. (l’altezza, funzione della frequenza, l’intensità, funzione dell’ampiezza; il timbro, risultante dai s. armonici che accompagnano il s. generatore; il modo di attacco, le cui caratteristiche sono legate al transitorio di attacco) si sono rivelate come elementi di un universo estremamente più complesso, le cui caratteristiche si stanno mostrando progressivamente all’analisi di scienziati e musicisti: risultante di questo processo di ricerca è, in campo strettamente musicale, un rivoluzionario ampliamento delle virtualità acustiche e tecniche dello strumento e della voce e una conseguente espansione delle possibilità di organizzazione del s. a livello compositivo.

Tecnica

Per la tecnica di registrazione e riproduzione dei suoni ➔ suono, registrazione e riproduzione del.