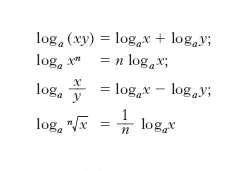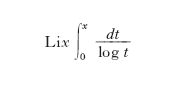logaritmo

Si definisce l. di un numero reale positivo x rispetto alla base a (reale, positiva e diversa da 1) l’esponente y che bisogna attribuire alla base a per ottenere il numero x; il l. di x nella base a si indica con log_ax. La scrittura y=log_ax equivale dunque a a^y=x; perciò il calcolo del l. è in un certo senso l’operazione inversa dell’elevamento a potenza (in altro senso l’operazione inversa dell’elevamento a potenza è l’estrazione di radice). Di conseguenza le proprietà dei l. riflettono quelle delle potenze; esse sono date dai teoremi espressi dalle seguenti formule, ove x, y, sono numeri reali positivi ed n è un intero relativo diverso da zero:

Si ha, inoltre, log_a a=1, log_a1=0. Non esiste il l. del numero 0 e neanche, nel senso della definizione ora data, il l. di un numero negativo. In molte questioni si assume come base a il numero e=2,718..., cioè il cosiddetto numero di Nepero (➔ Napier, John), e si hanno allora i l. naturali, o iperbolici, o neperiani; il log_ex si indica anche con lnx o con logx. D’altra parte, noto il l. di un numero in una base a, si calcola facilmente il l. dello stesso numero in un’altra base b mediante la formula log_bx=log_ba ∙ log_ax.

Calcolo con i logaritmi

L’uso dei l. è risultato molto vantaggioso per il calcolo numerico di espressioni contenenti prodotti, potenze, quozienti e radici, in quanto tali operazioni vengono sostituite rispettivamente da somme, prodotti, differenze, quozienti. L’uso dei l. nel calcolo numerico ha perso però via via interesse con il diffondersi dei calcolatori elettronici, in particolare di quelli da tavolo e tascabili. Usando sistematicamente la base a=10 (l. decimali, indicati brevemente con lg e con Log), si dice caratteristica di un l. il massimo intero, anche negativo, che non lo supera, mantissa la differenza (sempre positiva) tra il l. e la caratteristica. Per es., Log 20=1,30103: caratteristica 1, mantissa 30103. Uno dei vantaggi dei l. decimali nei calcoli consiste nel fatto che spostando la virgola decimale del numero non si altera la mantissa ma solo la caratteristica; il calcolo di quest’ultima è poi in ogni caso immediato (il numero delle cifre intere, diminuito di un’unità, se x ≥1; il numero degli zeri precedenti le cifre significative, ivi compreso quello prima della virgola, preso negativamente, se x < 1; per es., Log 732,41=2,...; Log 0,0014=−3,...). Per determinare la mantissa si usano le cosiddette tavole logaritmiche, tabelle che forniscono la mantissa, con un certo numero di cifre decimali (5 o 7 o più) dei numeri che hanno cinque cifre significative.

L. integrale

Si chiama l. integrale (J. Soldner, 1809) o iperlogaritmo (L. Mascheroni) o logologaritmo (I. Caluso), la funzione

prendendo la parte principale in 0. Essa ha grande importanza nella teoria dei numeri primi, quando gli estremi di integrazione sono 2 e n (numero naturale). Infatti è stato dimostrato che essa è asintotica alla funzione π(n), che fornisce il numero dei numeri primi inferiori a n. Il l. integrale, che s’indica anche con il simbolo lix e il cui grafico è sostanzialmente analogo a quello della funzione l. con asintoto verticale in x=1, è una funzione trascendente, non riducibile alle trascendenti elementari (funzioni trigonometriche ed esponenziali, logaritmo).

L. nel campo complesso

Dato il numero complesso z=x+iy=ρe^iϑ diverso da zero, si chiama l. naturale di z ogni soluzione w dell’equazione esponenziale e^w=z. Si ottiene w=log|z|+i arg z=log ρ+i(ϑ+2kπ) ove |z|=ρ è il modulo e arg z è l’argomento del numero complesso z. L’argomento di w è definito a meno della costante additiva 2kπ, con k intero arbitrario. In altre parole, il l. nel campo complesso è una funzione a infiniti valori, e ciò non sorprende in quanto è la funzione inversa dell’esponenziale, che, sempre nel campo complesso, è una funzione periodica. Spesso, per evitare questa ambiguità, si considera la cosiddetta determinazione principale del l.: essa si indica con Log z e si ottiene scegliendo la determinazione principale, indicata con Arg ϑ, dell’argomento ϑ, cioè quella per cui 0≤ϑ<2π. Si noti però che la funzione Log z è a un solo valore ma presenta discontinuità lungo la semiretta del piano complesso su cui si rappresentano i numeri reali positivi. Nell’insieme aperto ottenuto dal piano con la soppressione di tale semiretta la funzione Log z è continua e anzi olomorfa, con derivata 1/z (➔ serie).

Derivate, funzioni, scale, serie logaritmiche

fig. 1

fig. 2

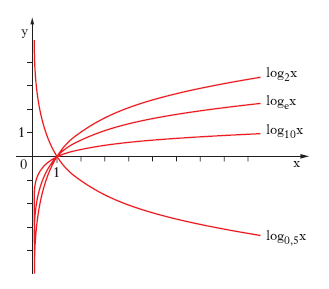
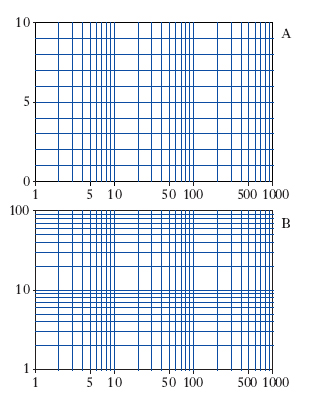
Derivata logaritmica di una funzione f(x) è la derivata del l. di f(x), ed è uguale al rapporto tra la derivata e la funzione: Dlog f(x)=f′(x)/f(x). Funzione logaritmica L. in una prefissata base, pensato in funzione del numero, che è la variabile indipendente y=log_ax. Si ha, per ogni a, log_a 1=0, log_aa=1; inoltre la funzione logaritmica è divergente sia per x=0 sia per x=∞. Precisamente, se a > 1 essa ha limite −∞ quando x tende a zero e +∞ quando x tende a +∞; viceversa, se a < 1. La funzione logaritmica è l’inversa della funzione esponenziale y=a^x. Il grafico della funzione l. è detto curva logaritmica (fig. 1). Scala logaritmica Scala graduata che si ottiene riportando sopra una retta, a partire da un’origine, segmenti (orientati) proporzionali ai l. dei numeri che si segnano all’estremo del relativo segmento. È logaritmica la scala che si usa nel regolo calcolatore. Nell’uso pratico si indicano con il nome di diagrammi a semplice o a doppia scala logaritmica, disegnati su apposita carta, detta rispettivamente carta logaritmica o carta semilogaritmica e carta doppiologaritmica, i diagrammi riferiti a un sistema di assi di riferimento nel quale si usa una scala l. su uno solo o su ambedue gli assi rispettivamente (fig. 2). Serie logaritmica È la serie

è convergente nel campo reale per −1 < x < 1. Si tratta della serie di Maclaurin della funzione y=log (1 + x).