Mascheróni, Lorenzo

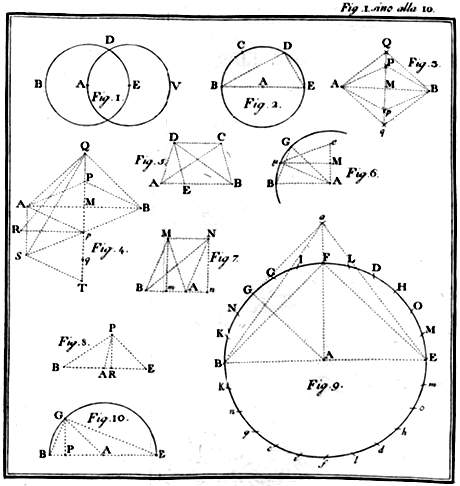
Matematico e poeta (Castagneta, Bergamo, 1750 - Parigi 1800). Vestì l'abito ecclesiastico a 17 anni e dal 1778 insegnò fisica e matematica al seminario di Bergamo. Per l'opera Nuove ricerche sull'equilibrio delle vòlte (1785) fu chiamato nel 1786 a insegnare algebra e geometria all'univ. di Pavia; divenne poi rettore di questa università (1789 e 1793) e dal 1788 al 1791 fu principe dell'Accademia degli Affidati. Ammiratore di Napoleone, fu nel 1797 uno dei deputati al corpo legislativo a Milano; inviato a Parigi, le vittorie degli Austro-Russi gli impedirono il ritorno. Fu tra i 19 firmatarî del memorandum a Napoleone che affermava per la prima volta i diritti dell'Italia. Parecchie le pubblicazioni cui dovette la sua fama di matematico: tra esse le Adnotationes ad calculum integrale Euleri (1790-92) e soprattutto la Geometria del compasso (1797), con dedica in versi a Napoleone, nella quale egli dimostra che ogni problema risolubile graficamente con riga e compasso è anche risolubile, facendo a meno della riga, con il solo compasso. Il nome di M. è anche legato alla costante di Eulero-Mascheroni di cui calcolò le prime 32 cifre decimali. Poeta, scrisse molto in latino e in italiano: ma il suo nome rimane legato soltanto all'elegante poemetto didascalico in versi sciolti, Invito a Lesbia Cidonia (1793), indirizzato alla contessa Paolina Grismondi (in Arcadia Lesbia Cidonia) per una visita all'orto botanico e ai musei scientifici dell'università di Pavia, che M. vede come una risorta Atene, centro di raccolta di artisti, scienziati e letterati.