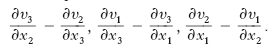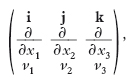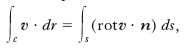rotore

matematica In analisi vettoriale si chiama r. di un campo vettoriale v(r), che abbia rispetto a una assegnata terna di riferimento Ox₁x₂x₃ componenti v₁, v₂, v₃, il vettore che rispetto alla medesima terna ha come componenti

Un metodo comunemente usato per ricordare l’espressione precedente è quello di pensare il r., seppure in maniera impropria, come determinante della matrice

dove i,j,k sono i versori degli assi x₁,x₂,x₃ rispettivamente. Ricorrendo all’operatore vettoriale nabla, ∇, di componenti

si può, più succintamente, scrivere:

Il r. di un vettore v, che si indica col simbolo rot v, trae la sua denominazione dal fatto che la rotazione rigida, variabile in generale da punto a punto, associata alla deformazione di un sistema continuo deformabile, resta individuata dal r. dello spostamento che il punto ha subìto nel passare dallo stato iniziale a quello finale. La divergenza di un r. e il r. di un gradiente sono sempre nulli; vale inoltre l’identità:

essendo ∇² l’operatore laplaciano. Altre proprietà del r. sono espresse dal teorema del r. e dal teorema di Stokes. Si consideri nel campo di definizione di v una superficie chiusa Σ e si indichino con n il versore della normale a Σ orientata verso l’esterno, con V il volume racchiuso da Σ; il teorema del r. si traduce nell’uguaglianza:

Il teorema di Stokes stabilisce invece l’uguaglianza tra la circuitazione di v estesa a una qualunque linea chiusa c del campo, in esso riducibile per deformazione continua a un punto, e il flusso di rotv attraverso una qualunque superficie regolare s avente la linea c per contorno:

dove il verso di percorrenza di c è antiorario rispetto a un osservatore che vede n puntare verso di sé. Se in ogni punto di un campo v (r) è rotv = 0, il campo si dice irrotazionale. Un campo irrotazionale semplicemente connesso è sempre conservativo (ammette un potenziale monodromo); se il campo è molteplicemente connesso, esso deriva ancora da un potenziale, però in generale non monodromo.

Tecnica

Nelle macchine, lo stesso che organo rotante. Il termine è di uso corrente per le macchine elettriche, in contrapposizione al termine statore che ne indica la parte fissa, e assume talvolta qualificazioni particolari: per es., r. avvolto e r. a gabbia si denominano i r. nelle macchine elettriche asincrone a seconda del tipo di avvolgimento.

Parte mobile dei condensatori variabili.

Organo sostentatore di particolari aeromobili, detti aeromobili a r. (elicotteri, convertiplani ecc.), costituito da due o più pale, in genere molto lunghe, con sezione a profilo alare.

Dispositivo propulsore costituito da un sistema a palette, rotante, caratteristico del propulsore cicloidale.

Nelle macchine termiche e idrauliche a canali aperti (turbine, pompe, compressori ecc.), sinonimo di girante o ruota.