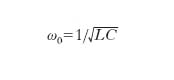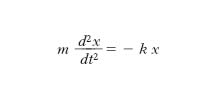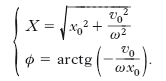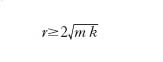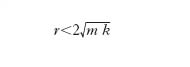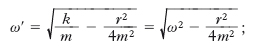oscillatore

In fisica e nella tecnica, dispositivo nel quale, una volta che sia stato convenientemente eccitato, si generano correnti elettriche oscillanti (o. elettrico) ovvero insorgono oscillazioni meccaniche (o. meccanico).

O. elettrici

Un o. elettrico fornisce una tensione e una corrente oscillanti utilizzando la potenza elettrica fornita da un generatore che di solito è un generatore di tensione continua. In questo senso l’o. può essere considerato un convertitore da continua ad alternata.

Gli o. possono essere classificati in vari tipi: in relazione alla forma della corrente oscillante possono essere distinti gli o. sinusoidali da quelli non sinusoidali (per es., generatori di onde quadre); questi ultimi basano l’inversione periodica del verso della corrente su fenomeni di scarica di condensatori su resistenze, per cui vengono anche chiamati o. a rilassamento, dei quali è un tipico esempio il multivibratore astabile. Si distinguono anche gli o. persistenti da quelli non persistenti o smorzati: nel primo caso l’ampiezza massima della tensione oscillante si mantiene costante nel tempo. Con riferimento alla frequenza della tensione prodotta si parla di o. a bassa, a media, ad alta e ad altissima frequenza; di o. a frequenza fissa o a frequenza variabile. Con riferimento alla potenza erogabile dall’o. senza pregiudizio per la persistenza delle oscillazioni, si parla di o. a bassa, a media, ad alta e ad altissima potenza. Con riferimento allo schema circuitale, si parla di o. a resistenza negativa, o. a reazione positiva, o. a rilassamento e o. bloccato.

fig. 1A

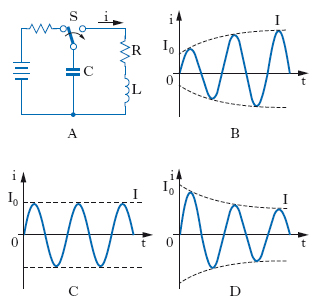
O. a resistenza negativa. - Si consideri il semplice circuito di fig. 1A e si immagini che il deviatore S sia spostato all’istante iniziale, quando il condensatore è carico alla tensione del generatore presente nel circuito: in queste condizioni appaiono oscillazioni libere nel circuito risonante RLC. Per questo circuito si può scrivere la seguente equazione differenziale:

che ammette la soluzione:

nella quale I₀ è il fattore di ampiezza della corrente nel circuito, α = R/2L è il fattore di smorzamento del circuito,

è la frequenza di risonanza e

è la frequenza naturale per le oscillazioni libere nel circuito. In relazione al valore negativo, nullo o positivo di α, le oscillazioni nel circuito possono essere di ampiezza crescente (fig. 1B), costante (fig. 1C) o decrescente (fig. 1D). In un o. sono presenti sempre delle perdite e, in generale, è richiesta una certa potenza da trasferire su un carico opportuno. D’altra parte, la necessità di generare oscillazioni di ampiezza costante richiede che il fattore di smorzamento α del circuito sia zero. Questo può essere ottenuto disponendo nel circuito, in serie al carico, un resistore non lineare che presenti un tratto a pendenza negativa nella sua caratteristica di corrente in funzione della tensione. In queste condizioni si possono instaurare oscillazioni persistenti in quanto, per un opportuno punto della caratteristica del resistore non lineare, si può ottenere che il fattore di smorzamento del circuito sia nullo, nel senso che risulta nulla la somma R delle resistenze in serie al circuito oscillante. Anzi, se il resistore non lineare presenta una resistenza differenziale tale che la somma delle resistenze nel circuito risonante, indicata con R, è minore di zero, le oscillazioni si innescano spontaneamente: in tal caso la loro ampiezza cresce fino a che il punto di lavoro del resistore non lineare non si sposta in un tratto in cui la resistenza differenziale è meno negativa e si realizza quindi il valore zero per la resistenza complessiva del circuito che è, come detto, la condizione per la realizzazione di oscillazioni persistenti di ampiezza costante.

Elementi circuitali che presentano tratti a pendenza negativa nella loro caratteristica di corrente in funzione della tensione sono tipicamente: archi elettrici (in aria libera o in tubi a scarica), tubi termoelettronici, diodi tunnel e transistori. Nei tratti a pendenza negativa all’aumentare della tensione la corrente diminuisce, contrariamente a quanto accade quando la resistenza è positiva, fatto che determina un incremento di potenza nel circuito, potenza che è in generale fornita da un opportuno generatore che polarizza la resistenza non lineare.

fig. 2

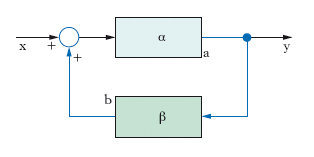
O. a reazione positiva. - Negli o. a reazione positiva, l’apporto di potenza necessario per il mantenimento delle oscillazioni è ottenuto attraverso un amplificatore reazionato (fig. 2): parte del segnale di uscita y dell’amplificatore a, che è reso di solito selettivo mediante l’introduzione sul carico di un circuito oscillante, viene riportata all’ingresso dell’amplificatore medesimo con la stessa fase del segnale x presente all’ingresso stesso. Dato che l’amplificatore è di solito invertente, per realizzare questa concordanza di fase, la rete di reazione b deve effettuare uno sfasamento di π. La condizione per l’innesco spontaneo delle oscillazioni nel circuito è αβ≥1 (condizione di Barkhausen), nella quale α è il guadagno dell’amplificatore e β è la frazione del segnale di uscita che è riportata all’ingresso. In generale le oscillazioni, una volta innescate, raggiungono rapidamente un’ampiezza che si mantiene poi costante. L’aumento dell’ampiezza è infatti limitato dalla caratteristica non lineare dell’amplificatore, il cui guadagno diminuisce all’aumentare dell’ampiezza delle oscillazioni, per cui si ottiene che, in condizioni di stabilità dell’ampiezza delle oscillazioni, αβ=1. Allo scopo di ottenere alto rendimento e alta potenza in uscita si fa normalmente funzionare l’amplificatore in classe C: il gruppo LC che rappresenta il carico dell’o. filtra la forma d’onda distorta generata dall’amplificatore e la riporta quindi a una famiglia di armoniche sinusoidali, nella quale la fondamentale ha ampiezza di gran lunga preponderante sulle armoniche superiori.

fig. 3

fig. 4

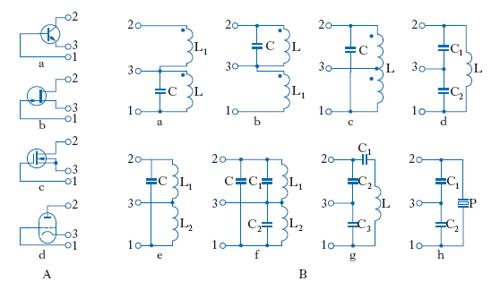
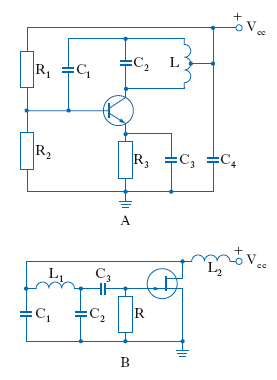
Gli o. a reazione positiva basati su circuiti LC sono di vari tipi, ma una schematizzazione può essere fatta tenendo presente che in tutti questi o. è presente un amplificatore. Questo amplificatore può essere (fig. 3) un transistore bipolare a, un transistore a effetto di campo JFET b o MOSFET c. Ai tre terminali dell’amplificatore si connette una delle diverse reti di reazione, mostrate nella fig. 3A: o. con accoppiamento a trasformatore a, b; o. ad autotrasformatore c; o. a partitore capacitivo (o. Colpitts) d; o. a partitore induttivo (o. Hartley) e, basato sullo stesso principio; per frequenze più elevate è richiesta una maggiore complessità circuitale per realizzare la partizione, come nel caso dei circuiti f e g, mentre, per maggiore stabilità di frequenza si ricorre a un risonatore piezoelettrico h. Esempi di oscillatori LC a reazione positiva sono dati in fig. 4.

fig. 5

fig. 6

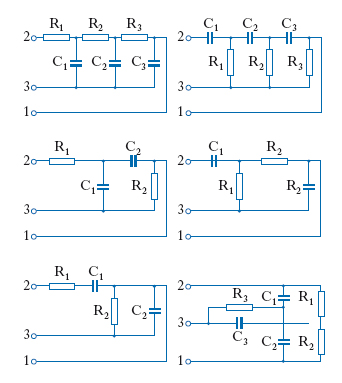
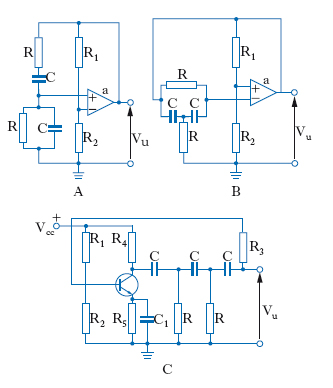
L’o. a resistenza e capacità è un o. a reazione positiva che ha come carico un circuito RC e come rete di reazione ancora un circuito RC. Quando l’amplificatore lavora in classe C, si può avere un notevole contenuto di armoniche, proprio perché i circuiti RC effettuano una minore azione di filtraggio rispetto ai circuiti LC. Esempi di reti di reazione per o. RC sono dati nella fig. 5. Anche in questo caso la rete di reazione deve realizzare uno sfasamento di π (o di 2π, se l’amplificatore non è invertente) per riportare il segnale di reazione in fase con il segnale presente all’ingresso. Esempi di o. RC a reazione positiva sono riportati nella fig. 6.

L’o. bloccato (o a bloccaggio) è costituito da un o. a reazione positiva il cui amplificatore è governato dalla tensione di carica di un condensatore. Quando il condensatore è scarico, l’amplificatore dà un segnale di uscita che però carica il condensatore e porta di nuovo all’interdizione dell’amplificatore. Quindi il condensatore si scarica su un’opportuna resistenza e il ciclo si ripete. Essendo presenti un circuito oscillante e una reazione positiva, durante i periodi di funzionamento dell’amplificatore viene prodotta un’oscillazione alla frequenza di accordo del circuito oscillante. Il tempo di ripetizione del ciclo è invece controllato dal prodotto RC del gruppo resistenza-condensatore di controllo.

Stabilità in frequenza. - Il problema della stabilità in frequenza è di fondamentale importanza per gli o. persistenti. Infatti, nella tecnica delle telecomunicazioni (specialmente in radiotecnica) e genericamente in elettronica nei circuiti di clock, si fa uso di o. persistenti come o. di riferimento. Realizzare un o. che fornisca un’oscillazione a una data frequenza costante nel tempo non è facile: variazioni di temperatura, deformazioni meccaniche di certi componenti, variazioni delle tensioni di alimentazione, variazioni del carico, sono alcune delle cause che inducono spostamenti della frequenza dell’oscillatore. È quindi necessario ricorrere a particolari accorgimenti costruttivi che mirino a ottenere circuiti oscillanti LC o circuiti di sfasamento RC particolarmente stabili. Nel caso di circuiti oscillanti LC si ottiene una maggiore stabilità se è molto grande il fattore di merito del circuito, se cioè si hanno basse perdite resistive. Per gli o. a frequenza più alta, i circuiti LC sono sostituiti da linee o cavità risonanti. Per gli o. a frequenza fissa, si ricorre a risonatori di tipo meccanico: diapason o barrette di acciaio per le basse frequenze, cristalli piezoelettrici che risuonano in fondamentale o in armonica per le frequenze più alte. In questo caso è necessario un opportuno trasduttore che converta l’energia elettrica in energia meccanica e viceversa. Si sfruttano a tale scopo l’accoppiamento elettromagnetico (per basse frequenze), l’effetto magnetostrittivo (per medie e basse frequenze) e l’effetto piezoelettrico (per alte frequenze). Il fattore di merito di questi o. meccanici è particolarmente elevato, mentre il coefficiente di temperatura può essere mantenuto molto basso utilizzando materiali con caratteristiche particolari. Per eliminare instabilità di frequenza dovute a variazioni del carico, si usa interporre un separatore che presenti all’o. un’impedenza costante.

Un tipo particolare di o. elettrico è l’o. ECO (electron-coupled oscillator «o. ad accoppiamento elettronico»), costituito da un tubo termoelettronico multigriglia in cui l’accoppiamento fra entrata e uscita è affidato alla corrente elettronica nel tubo.

O. meccanici

fig. 7

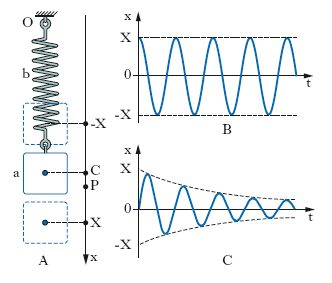
Un o. meccanico è un dispositivo in cui possono destarsi ed eventualmente mantenersi oscillazioni meccaniche (lineari o angolari, oppure di pressione ecc.). Un dispositivo di questo tipo è, per es., quello costituito da una massa a (fig. 7) appesa, tramite una molla b, a un punto fisso O; la massa, tirata (o spinta) verticalmente e poi abbandonata a sé stessa, prende a oscillare intorno alla posizione di quiete; in queste oscillazioni si ha una continua e reciproca trasformazione di energia cinetica della massa in energia potenziale elastica della molla, salvo la parte di energia che a ogni oscillazione viene dissipata in calore a causa della resistenza dell’aria e di attriti interni nella molla. Si ha una perfetta analogia formale con un circuito oscillante elettrico: l’induttanza di questo corrisponde alla massa, la capacità corrisponde alla cedevolezza della molla, la resistenza elettrica corrisponde alla resistenza meccanica. L’o. della fig. 7A può essere schematizzato come un punto materiale P, di massa m, libero di muoversi lungo una traiettoria rettilinea e soggetto, se spostato dalla sua posizione di equilibrio C, a una forza costantemente rivolta verso C (centro del moto) e di intensità proporzionale, secondo una costante positiva k, alla distanza di P da C (forza di richiamo elastica: nel caso specifico, quella esplicata dalla molla b sulla massa a). In un sistema di ascisse rettilinee x, con origine in C, se si assumono nulle le resistenze al moto di P, il moto è descritto dall’equazione differenziale

[1] formula,

essendo t il tempo; integrando, si ottiene: x=X cos (ωt−ϕ) dove X, ampiezza del moto, è la massima elongazione di P da C, ω la pulsazione e ϕ la fase iniziale. Delle tre grandezze che caratterizzano il moto, la pulsazione ha il valore

[2] formula,

cui corrisponde il periodo T = 2π/ω, dipendente dunque dalle caratteristiche meccaniche del sistema, mentre l’ampiezza e la fase iniziale dipendono dalle condizioni iniziali, cioè dalla posizione x₀ e dalla velocità v₀ che competono a P nell’istante iniziale t = 0; si ha precisamente:

[3] formula.

In questo caso P, che esegue un moto oscillatorio permanente, costituisce un o. armonico non smorzato. In particolare se è v₀ = 0, per x si ha l’andamento temporale illustrato nella fig. 7B. In pratica, però, occorre tenere conto delle inevitabili resistenze al moto, e ciò viene fatto introducendo nella [1] un termine rappresentante una forza resistente, diretta in verso contrario al moto. Nella maggior parte dei casi tale forza può assumersi proporzionale secondo una costante positiva r, alla velocità dx/dt di P; la [1] assume allora la forma:

,

ovvero, tenendo presente la [2]

[4] formula.

La soluzione della [4] è del tipo

,

dove d₁ e d₂ sono le radici dell’equazione algebrica d²+(r/m)d+ω²=0, e c₁, c₂ sono costanti da determinare in base alle condizioni iniziali. Se è soddisfatta la condizione r²≥4m²ω², cioè se

,

d₁ e d₂ sono radici reali (eventualmente coincidenti) e il moto è aperiodico: P tende asintoticamente a portarsi dalla posizione iniziale verso il centro C; se invece è

,

d₁ e d₂ sono radici complesse coniugate e la soluzione assume la forma:

[5] formula,

essendo

[6] formula;

X e ϕ, ampiezza iniziale e fase iniziale, sono determinabili a partire dalle condizioni iniziali. P è animato da un moto periodico la cui ampiezza Xexp[–(r/2m)t] diminuisce esponenzialmente nel tempo, cioè è animato da un moto oscillatorio smorzato, pseudo-periodico: esso costituisce un o. smorzato. La pulsazione è leggermente minore di quella che, a parità di altre condizioni, si avrebbe in assenza di forza resistente; peraltro essendo r², in genere, molto minore di 4m², si può, con buona approssimazione, assumere ω′=ω. Così facendo, per la determinazione di X e ϕ si possono usare le [3]; in particolare, se v₀=0 si ha x=Xexp[−(r/2m)t]cos(ωt): il diagramma di tale funzione è riportato nella fig. 7C. O. il cui comportamento è descritto dalle relazioni precedentemente ricordate sono non solo quelli rettilinei a massa e molla, ma anche i pendoli, che possono essere riguardati come o. curvilinei, e anche o. rotativi, costituiti da un volano collegato con una molla a spirale (per es., i bilancieri degli orologi). Molto più complesso è, invece, il caso di o. costituiti da corde, lamine, membrane elastiche o da masse elastiche (per es., la massa d’aria racchiusa in un tubo), in cui si destano oscillazioni che in genere non sono armoniche e vanno piuttosto riguardate come conseguenti alla propagazione di onde elastiche.

Se nell’o. meccanico sopra descritto la forza di richiamo non è una funzione lineare della distanza di P da C, l’o. si dice anarmonico, e il suo moto è una funzione del tempo piuttosto complicata, periodica ma con periodo dipendente dall’ampiezza. L’o. è poi, in generale, anarmonico quando su di esso agiscano forze resistenti dipendenti dalla velocità. In ogni caso, per ottenere un regime oscillatorio permanente, occorre compensare l’effetto delle resistenze passive, fornendo via via al dispositivo l’energia dissipata per tale causa. Ciò può farsi in vari modi. Per es., o. persistenti sono ottenuti, come negli orologi, applicando a un bilanciere o a un pendolo un meccanismo di scappamento, il quale, comandato dall’o. medesimo e azionato da un motore (a molla o di altro tipo), imprime al sistema oscillante impulsi che mantengono costante l’ampiezza delle oscillazioni; oppure, come si fa negli o. a diapason, si ricorre a dispositivi elettromagnetici o elettronici.