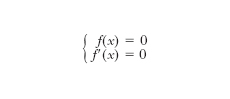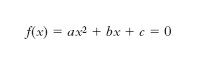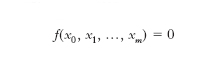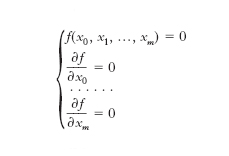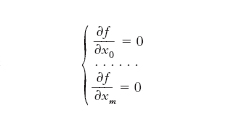discriminante
In matematica, d. di un’equazione algebrica f(x)=0 di grado n, è una funzione razionale intera dei coefficienti dell’equazione, il cui annullarsi è condizione necessaria e sufficiente perché l’equazione stessa abbia una radice almeno doppia. Giacché una radice almeno doppia della f(x)=0 è radice anche dell’equazione f′(x)=0 (dove f′ è la derivata prima di f), e viceversa ogni radice comune alle due equazioni f(x)=0 e f′(x)=0 è almeno doppia per la prima, il d. di f(x)=0 non è altro, a meno di un fattore numerico, che il risultante (➔) del sistema
[1] formula.
Nel caso dell’equazione di 2° grado
,
il d. ha l’espressione D=b2 - 4 a c, e il suo annullarsi è appunto condizione necessaria e sufficiente perché le due radici dell’equazione coincidano in una radice doppia. Inoltre, quando a, b, c sono reali, se D >0 le due radici sono reali e distinte, se D 〈0 sono complesse coniugate. D. dell’equazione algebrica omogenea
[2] formula
è, analogamente, una funzione razionale intera dei coefficienti dell’equazione il cui annullarsi denota che nello spazio a m dimensioni l’ipersuperficie [2] possiede almeno un punto doppio. Il d. è perciò dato, a meno di un fattore numerico, dal risultante del sistema, analogo al sistema [1]:
o anche, per il teorema di Eulero sulle funzioni omogenee, dal risultante del sistema: