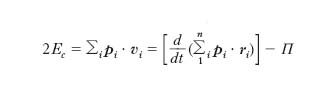viriale

In fisica, termine, introdotto da R.J.E. Clausius, per indicare la quantità

Π = Σⁿ_1ir_i ∙ F_i, dove r_i è il raggio vettore

del generico punto di un sistema materiale e F_i la forza agente su di esso. Teorema del v. Se E_c è l’energia cinetica di un sistema, p_i la quantità di moto, v_i la velocità dell’i-esimo punto materiale, si ha

facendo la media temporale di questa uguaglianza su un intervallo di tempo tendente a infinito, se i punti del sistema si muovono in una regione finita dello spazio con velocità finite (di modo che la media del termine contenuto nella parentesi quadra tenda a zero) si ha (teorema del v.) 2E̅_c=−Π̅, dove la sopralineatura indica la media temporale. Se le forze agenti sui punti del sistema sono conservative e l’energia potenziale E_p è una funzione omogenea di grado k di tutti i raggi vettori, si ottiene infine la relazione 2Ē_c=kĒ_p, che, introducendo l’energia meccanica totale E=Ē=E_c+E_p, può essere scritta nella forma Ē_p=2E/(k+2), o anche Ē_c=kE/(k+2). Applicando questo risultato al caso di forze elastiche (k=2) si ha: Ē_c=Ē_p; per interazioni di tipo newtoniano e coulombiano (k=−1) si ha 2Ē_c=−Ē_p e quindi E=−Ē_c (il moto si svolge in una regione finita solo se l’energia meccanica totale è negativa).