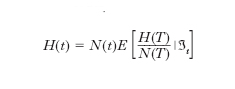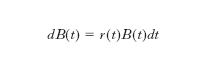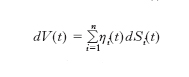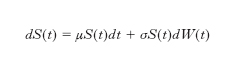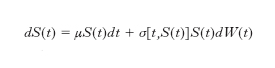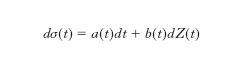finanziaria, matematica

Teoria matematica della capitalizzazione e attualizzazione; ha come fondamento il fatto che nell’economia mercantile il capitale produce un interesse.

Cenni generali

Per mezzo di funzioni di capitalizzazione e attualizzazione vengono formalizzati criteri di valutazione nell’impiego di capitali e in operazioni f. (acquisto di fabbricati, di titoli, assicurazioni, prestiti ecc.). Dal punto di vista matematico, la capitalizzazione, cioè il processo di trasformazione dell’interesse prodotto in capitale, si realizza attraverso tre possibili leggi: a) la capitalizzazione semplice, che avviene quando gli interessi via via maturati dal capitale non sono trasformati in capitale (non divengono fruttiferi); b) la capitalizzazione composta, che si ha quando gli interessi sono aggiunti al capitale divenendo fruttiferi, a intervalli di tempo costanti (il più frequentemente, ogni anno); c) la capitalizzazione continua, che si ha quando gli interessi si capitalizzano appena prodotti, sono cioè aggiunti al capitale, per così dire, a intervalli di tempo infinitesimi.

Definito come interesse il reddito prodotto dal capitale, si chiama tasso o saggio d’interesse (teorico) l’interesse prodotto dal capitale unitario nell’unità di tempo, che è per solito l’anno (nella pratica si usa il tasso percentuale, pari a 100 volte il tasso teorico, pari cioè all’interesse prodotto da 100 unità capitale – per es., 100 euro – nell’unità di tempo), mediante la regola della capitalizzazione semplice o composta. I due problemi tipici che si pongono nella matematica f. sono allora i seguenti: a) Dato il capitale (iniziale), il tasso d’interesse, il tempo t per il quale il capitale è stato impiegato, determinare il montante dopo il tempo t, cioè l’ammontare del capitale aumentato degli interessi maturati nel tempo t. La risposta dipende naturalmente dalla legge di capitalizzazione adottata (➔ interesse). b) Dato il montante (come somma S dovuta tra t anni) e il tasso d’interesse, determinare il capitale C, cioè il valore attuale della somma S. Anche in questo caso, la risposta dipende dal tipo di legge di capitalizzazione; intervengono i concetti di sconto e tasso di sconto, legati a quelli di interesse e tasso d’interesse (lo sconto, S-C, è l’interesse prodotto in t anni dal valore attuale C della somma S dovuta tra t anni).

Gli studi su rendita, annualità e ammortamento, che costituiscono altrettanti capitoli della matematica f., sono sempre legati ai concetti fondamentali ora accennati di capitale, interesse, montante, tempo, tasso d’interesse ecc., e alle loro relazioni analitiche nelle varie leggi di capitalizzazione.

I prodotti derivati

Nella seconda metà del 20° sec., la matematica f. ha cominciato a far uso di strumenti matematici sempre più complessi a tal punto da evolvere in una vera e propria nuova branca chiamata finanza matematica, che si occupa principalmente della definizione e valutazione di prodotti finanziari complessi: i titoli derivati. I prodotti derivati sono titoli finanziari il cui rendimento è aleatorio e dipendente dall’evoluzione di alcuni titoli base (attività) sottostanti. Esempi fondamentali sono rappresentati dai contratti forward e dalle opzioni europee. I forward sono contratti per cui a una prefissata data futura T un certo titolo finanziario, di valore S(T) al tempo T, viene scambiato (comprato o venduto) a un prezzo prefissato K, determinando per il compratore un risultato economico a scadenza (guadagno o perdita) pari a S(T)−K, e per il venditore un saldo uguale e contrario. Le opzioni europee sono contratti simili, che conferiscono il diritto ma non l’obbligo di comprare o vendere il titolo sottostante al prezzo K alla data T. Nel caso di un’opzione di tipo call, il diritto è a comprare, con risultato economico a scadenza pari a max(S(T)−K,0), dove max(a,b) indica il massimo tra i due numeri reali a e b. Per un’opzione di tipo put, il diritto è a vendere, con risultato economico a scadenza pari a max(K-S(T),0).

La valutazione dei prodotti derivati si basa su teorie di finanza matematica sviluppate all’inizio degli anni 1970, anche se alcuni concetti fondamentali furono introdotti già all’inizio del 20° secolo.

L’assenza di arbitraggio. -Il principio fondamentale su cui si fonda la teoria è costituito dall’assenza di arbitraggio, cioè dall’impossibilità di realizzare un guadagno quasi certo nel futuro a partire da un investimento iniziale nullo. In termini matematici, si dimostra che l’assenza di arbitraggio risulta equivalente, sotto opportune ipotesi, all’esistenza di un numerario (unità di conto, cioè titolo finanziario di valore strettamente positivo, che non paga dividendi o altri flussi, e che viene utilizzato per normalizzare il valore degli altri titoli dell’economia di riferimento) e di una misura di probabilità associata, rispetto alla quale qualunque titolo scambiabile nell’economia ha un valore che diviso per quello del numerario risulta una martingala (processo stocastico integrabile i cui valori futuri sono in media uguali al valore corrente del processo stesso). In formule, indicando con N(t) il valore del numerario al generico tempo t, il prezzo H(t) al tempo t di un derivato che paga H(T) al tempo T risulta dato da:

dove ℑ_t rappresenta la sigma-algebra generata dalle variabili finanziarie in questione fino al tempo t, ovvero l’informazione sui dati di mercato disponibile a tale data, ed E denota il valore atteso rispetto alla misura di riferimento. Storicamente, il primo e più importante numerario a essere considerato, fu il deposito bancario con ribilanciamento continuo, il cui valore B(t) soddisfa l’equazione differenziale ordinaria

dove r(t) è il tasso di interesse istantaneo, che in generale è stocastico, ma che in molte applicazioni viene ipotizzato deterministico. La misura di prezzatura associata a B viene chiamata ‘misura neutrale al rischio’, perché, per sua stessa definizione, ogni attività di mercato ha, relativamente a essa, un rendimento istantaneo medio uguale a r(t) (nel caso di assenza di dividendi o altri flussi).

La replica dinamica. - L’altro concetto fondamentale su cui si fonda la teoria della valutazione dei derivati è costituito dalla replica dinamica. Per replica dinamica si intende la possibilità di individuare un portafoglio di attività f. che costituiscono l’economia di riferimento, le cui componenti vengono ribilanciate in tempo continuo in modo auto-finanziante (le variazioni di valore del portafoglio sono solo dovute alla variazione dei prezzi di mercato) e così da replicare perfettamente il risultato economico a scadenza del derivato. Indicando con S_i il prezzo dell’attività i-esima, i=1...n, con n numero delle attività di mercato, la strategia che consiste nel detenere η_i(t) unità di S_i al tempo t, il cui valore è indicato con V(t), risulta auto-finanziante se e solo se

e replicante il risultato economico a scadenza H(T) se e solo se V(T)=H(T) q.c. I differenziali che compaiono nella formula precedente sono differenziali stocastici, dal momento che sia V che ogni S_i sono processi stocastici a tempo continuo. Il più tipico processo stocastico utilizzato in finanza matematica è il moto browniano geometrico, definito dalla seguente equazione differenziale stocastica

dove μ è il tasso (costante) di rendimento istantaneo medio, σ è il coefficiente (costante) di volatilità del processo e W è un moto browniano standard (processo continuo a incrementi indipendenti e normalmente distribuiti). Il moto browniano geometrico è il processo stocastico ipotizzato da F. Black, M. Scholes e R. Merton (➔ Black-Scholes, formula di). Con lo sviluppo dei mercati finanziari, e delle opzioni in particolare, si è resa necessaria l’introduzione di modelli più sofisticati in grado di recuperare, in modo coerente e simultaneo, i prezzi delle opzioni europee quotate in un dato mercato. A tal fine, nella letteratura finanziaria, sono state proposte varie estensioni del moto browniano geometrico di Black e Scholes e Merton. La prima consiste nel rimpiazzare il coefficiente costante σ con una funzione deterministica σ[t,S(t)], trasformazione del tempo e del livello dell’attività stessa, producendo la dinamica

che viene definita a volatilità locale. La seconda estensione, che trova ampie applicazioni in pratica, è costituita dai modelli a volatilità stocastica, in cui si ipotizza che il coefficiente di volatilità segua una propria equazione differenziale stocastica:

con a e b processi stocastici adattati e Z moto browniano, correlato (istantaneamente) con W. Ulteriori alternative si basano sull’introduzione di salti, modellati per esempio con un processo di Poisson, o sulla sostituzione dei moti browniani nelle dinamiche precedenti con più complessi e generali processi di Levy.

Differenze tra modelli di tasso d’interesse. - Ai fini della valutazione di prodotti derivati, dinamiche a volatilità locale o stocastica vengono tipicamente utilizzate per modellare l’evoluzione dei titoli sottostanti nei mercati dell’azionario e dei tassi di cambio. Nel mercato dei tassi di interesse, la situazione è complicata dal fatto che il sottostante sia, in generale, l’intera curva dei tassi di interesse, cosicché le attività da modellare non risultano identificabili in modo univoco. In letteratura, pertanto, sono stati proposti approcci differenti a seconda dei tassi di interesse che si è scelto di modellare. Tradizionalmente, i primi modelli di tasso di interesse, introdotti negli anni 1970 e 1980, si basarono sul tasso istantaneo r(t), la cui evoluzione venne postulata direttamente nella misura neutrale al rischio. Successivamente, alla fine degli anni 1980, fu sviluppata una modellistica di tasso forward istantaneo, basata sull’evoluzione dell’intera curva dei tassi di interesse, e che risulta particolarmente idonea a definire un’intelaiatura generale da cui far discendere opportune specificazioni. Dalla fine degli anni 1990, supportata dai risultati teorici sul cambio di numerario, si è diffusa una modellistica di tasso forward a composizione semplice, che permette di modellare direttamente variabili di mercato, consentendo inoltre una calibrazione automatica ai caplet (opzioni call su tassi LIBOR ➔) quotati dal mercato stesso. Relativamente al mercato del credito, la modellistica per la valutazione dei derivati si è sviluppata solo a partire dalla fine degli anni 1990, per prodotti dipendenti da una sola o più attività soggette a rischio di fallimento. I modelli utilizzati si dividono prettamente in due categorie. La prima è costituita dai modelli strutturali, in cui vengono modellati i valori delle attività in modo analogo a quello di un mercato azionario e in cui il fallimento viene identificato col superamento, dall’alto, di una data barriera di prezzo. La seconda categoria è rappresentata dai modelli a intensità (o a forma ridotta) in cui viene modellato il tempo di fallimento come l’istante di primo salto di un processo di Poisson. Nel caso di più attività sottostanti, la dipendenza tra opportune trasformazioni dei tempi di fallimento associati a esse, viene tipicamente modellata con delle funzioni di copula.