Errore

Diritto

1. Diritto civile

Nel diritto civile l’e. costituisce una ipotesi di anormalità nella esplicazione dell’autonomia privata e nei relativi regolamenti d’interessi, i quali conseguentemente si presentano viziati o da una deficiente consapevolezza dell’oggettivo significato del negozio posto in essere o da una inconsapevolmente falsa rappresentazione della realtà reagente sul processo di formazione della volontà. Nel primo caso l’e., detto ostativo o nella dichiarazione (art. 1433 c.c.), consiste nel verificarsi di una differenza tra il significato che la parte attribuisce alla propria manifestazione di volontà (dichiarazione o comportamento) e il significato oggettivo della medesima, e produce un difetto di consapevolezza e di volontà in ordine alla manifestazione effettuata dal suo autore. L’e. ostativo può dipendere da cause interne al dichiarante (distrazione, ignoranza del vero significato delle espressioni adottate) o esterne al medesimo quando il dichiarante si avvalga dell’opera di terzi nell’esprimere o recapitare la dichiarazione e questi terzi alterino il significato della volontà del dichiarante.

Le conseguenze giuridiche dell’e. ostativo sono le stesse che si producono a seguito dell’e. di vizio, che si ha quando l’autore di un negozio si determina al medesimo sulla base di un erroneo giudizio circa la concreta situazione di fatto; così la volontà si forma e si manifesta in una direzione diversa da quella che sarebbe stata seguita se l’interessato avesse avuto una cognizione corretta della realtà e una previsione adeguata dei fini da perseguire in quella situazione (art. 1428-1429, 1431 c.c.).

Si distingue normalmente l’e. di fatto dall’e. di diritto, vertendo il primo sopra un elemento della situazione di fatto, oggetto di rappresentazione e valutazione da parte dell’interessato, e comprendente il contenuto, i presupposti e le condizioni del previsto regolamento d’interessi, il secondo sopra un elemento normativo influente sulla fattispecie considerata; l’e. di diritto e espressamente considerato dall’art. 1429 c.c. nel senso di una limitazione della sua rilevanza alla sola ipotesi in cui sia stato ragione unica o principale del negozio. La transazione non può essere invece annullata per e. di diritto relativo alle questioni che sono state oggetto di controversia tra le parti (art. 1969 c.c.). L’e. di calcolo rappresenta una specie particolare e non ha di regola rilevanza ai fini di una valutazione critica del negozio, ma da luogo a semplice rettificazione, a meno che non si concreti in un e. di quantità e sia stato determinante l’intento dell’autore dell’atto (art. 1430 c.c.). Il trattamento normativo degli effetti dell’e. differisce a seconda del negozio che ne risulta viziato.

Nel matrimonio l’e. può provocare l’annullamento del vincolo qualora sia tale da escludere il consenso, ipotesi, questa, che si verifica soltanto quando l’e. cada sull’identità fisica dell’altra persona (art. 122 c.c.) o si tratti di e. essenziale su qualità personali dell’altro coniuge. L’e. sulle qualità personali e essenziale qualora, tenute presenti le condizioni dell’altro coniuge, si accerti che lo stesso non avrebbe prestato il suo consenso se le avesse esattamente conosciute e purché l’e. riguardi: a) l’esistenza di una malattia fisica o psichica o di una anomalia o deviazione sessuale, tali da impedire lo svolgimento della vita coniugale; b) l’esistenza di una condanna per delitto non colposo alla reclusione non inferiore a cinque anni, salvo il caso di intervenuta riabilitazione prima della celebrazione del matrimonio o sempre che l’azione di annullamento sia proposta prima che la sentenza sia divenuta irrevocabile; c) la dichiarazione di delinquenza abituale o professionale; d) la circostanza che l’altro coniuge sia stato condannato per delitti concernenti la prostituzione a pena non inferiore a due anni; e) lo stato di gravidanza causato da persona diversa dal soggetto caduto in e., purché ci sia stato disconoscimento ai sensi dell’art. 233 c.c., se la gravidanza e stata portata a termine.

Nelle successioni mortis causa l’e. non ha effetto in tema di accettazione dell’eredità (art. 483 c.c.), mentre può determinare l’annullamento dell’atto in tema di testamento: a quest’ultimo proposito l’art. 624 c.c., oltre a prevedere l’impugnabilità del testamento quando sia effetto di e., estende l’invalidazione alla disposizione testamentaria viziata da e. sul motivo (di fatto e di diritto) in quanto risultante dal testamento e purché unica ragione della disposizione di ultima volontà.

Nei contratti l’e. e causa di annullamento quando cada su elementi essenziali del negozio e sia riconoscibile da parte dell’altro contraente (art. 1428 c.c.): l’e. e pertanto essenziale se abbia determinato una falsa rappresentazione circa la natura o l’oggetto del contratto, circa l’identità dell’oggetto della prestazione ovvero una qualità che debba ritenersi determinante il consenso secondo il comune apprezzamento e le circostanze, circa l’identità o le qualità dell’altro contraente purché determinante il consenso (art. 1429 c.c.); l’e. e poi riconoscibile quando una persona di normale diligenza avrebbe potuto rilevarne la presenza nel corso della conclusione del contratto, avendo riguardo al contenuto, alle circostanze e alla qualità dei contraenti (art. 1431 c.c.). Il contratto viziato può essere annullato a domanda della parte incorsa in e., entro 5 anni dal momento in cui l’e. sia stato scoperto (art. 1442, 2° co., c.c.) e purché l’altra parte, prima che dall’atto possa derivare un pregiudizio, non offra di darvi esecuzione in modo conforme a quella che sarebbe stata la volontà contrattuale senza l’influenza causale dell’e. (art. 1432 c.c.).

2. E. giudiziario

Introdotto per la prima volta nel c.p.p. con riguardo alla riparazione per l’ingiusta custodia cautelare, l’e. giudiziario e il fatto determinante l’ingiusta detenzione e si riconosce al condannato prosciolto in sede di revisione se non ha contribuito a causarlo con dolo o colpa grave. In tal caso egli ha diritto, a norma dell’art. 643 c.p.p., a una riparazione commisurata alla durata dell’eventuale espiazione della pena o internamento e alle conseguenze personali e familiari derivanti dalla condanna. Oltre che per l’aspetto negativo dell’assenza di qualunque contributo causale alla realizzazione dell’e. giudiziario, il titolo su cui si fonda il diritto alla riparazione si caratterizza per l’aspetto positivo della sentenza di assoluzione con la quale deve concludersi il giudizio di revisione. La riparazione si attua mediante il pagamento di una somma di denaro ovvero, tenuto conto delle condizioni dell’avente diritto e della natura del danno, mediante la costituzione di una rendita vitalizia. L’avente diritto può inoltre essere accolto, su sua domanda, in un istituto a spese dello Stato. In caso di morte del condannato, anche prima del procedimento di revisione, il diritto alla riparazione spetta al coniuge, ai discendenti e ascendenti, ai fratelli e sorelle, agli affini entro il primo grado e alle persone legate con vincolo di adozione a quella deceduta. La somma e ripartita equitativamente e non può essere maggiore di quella che sarebbe stata liquidata al prosciolto. La domanda di riparazione e proposta, a pena di inammissibilità, entro due anni dal passaggio in giudicato della sentenza di revisione e su di essa decide la corte di appello in camera di consiglio ex art. 127 c.p.p. L’ordinanza che decide sulla domanda e comunicata al pubblico ministero e notificata a tutti gli interessati, i quali possono ricorrere per cassazione. Se nel giudizio di revisione si dimostra che la condanna e stata pronunciata in conseguenza di falsità in atti o in giudizio o di un altro fatto di reato, qualora lo Stato abbia corrisposto la riparazione, esercita il diritto al risarcimento dei danni contro il responsabile fino alla concorrenza della somma pagata.

Filosofia

In quanto appartenente alla sfera del giudizio (➔) e cioè alla sfera degli atteggiamenti valutativi, si può chiamare e. in generale ogni giudizio o valutazione che contravvenga al criterio ammesso come valido nel campo a cui il giudizio si riferisce, o ai limiti di applicabilità del criterio stesso. Nella storia della filosofia sono significative al riguardo le dottrine di Platone e Aristotele che fissarono i termini delle successive teorizzazioni. Platone sviluppo una teoria secondo la quale l’e. e una combinazione di forme (generi e specie) effettuata in deroga alle leggi della dialettica. Anche per Aristotele l’e. si dà solo là dove elementi diversi vanno combinati e quindi può verificarsi quando l’intelletto, che deve effettuare detta sintesi, non opera rispettando la struttura sostanziale dell’essere. In tal modo l’e. viene ascritto alla sfera delle affermazioni accidentali ed e quindi fuori della scienza.

Dopo Aristotele, al problema dell’e. si diedero in sostanza due soluzioni fondamentali. Secondo la prima, l’e. non esiste perché e una ‘non conoscenza’ e un ‘non essere’, o comunque qualcosa di negativo e accidentale destinato a scomparire; la seconda soluzione fa scaturire l’e. dall’intervento di una forza estranea che viene a disturbare il regolare funzionamento dell’intelletto nella formulazione del giudizio. Tale forza e indicata ora nella volontà, ora nella sensibilità. La filosofia contemporanea riconduce il problema dell’e. alla tesi del fallibilismo, che nega la possibilità di ottenere una conoscenza certa.

Fisica

1. E. di osservazione o di misurazione

Eseguendo più volte, con un certo strumento, e nelle stesse condizioni, la misurazione di una grandezza fisica X, si osserva sperimentalmente che i valori rilevati xi della grandezza stessa sono fra loro diversi; nasce quindi il problema di risalire al valore vero x* della grandezza misurata: ciò non è però possibile e si può arrivare tutt’al più a una stima x0 (detta valore più probabile) della grandezza misurata; occorre allora determinare l’attendibilità di x0, cioè occorre determinare la precisione della misurazione (ovvero dello strumento utilizzato); la precisione e inversamente proporzionale all’e. ε, definito in modo che, con una prefissata probabilità, sia: x0G ε . x* . x0+ ε (ovvero: x* = x0 ± ε); questa relazione mostra come il valore della grandezza e compreso (con la prefissata probabilità) nell’intervallo di ampiezza 2ε (di cui x0 e il valore centrale) che prende nome di incertezza della misurazione o dello strumento. Nel caso in cui la suddetta probabilità è uno, l’e. e detto e. massimo.

Nelle considerazioni che seguono si suppone che lo strumento utilizzato non perturbi la grandezza in esame, cioè che non vngano commessi e. di inserzione, e che la grandezza da misurare sia costante nel tempo e che pertanto non vengano commessi e. di rapidita. Ciò premesso, si definisce e. di una misura (o e. assoluto) la differenza algebrica fra il valore misurato e il valore vero (incognito) di una grandezza: εi = xi G x*; si definisce inoltre e. relativo il rapporto fra l’e. assoluto e il valore della grandezza; si osservi che mentre l’e. assoluto ha le stesse dimensioni della grandezza da misurare, l’e. relativo e adimensionato e si esprime generalmente in percentuale.

L’e. di una misura può essere di due tipi: e. sistematico ed e. accidentale (o casuale). L’e. sistematico può essere provocato da uso non corretto dello strumento da parte di chi effettua la misura (e. personale), dall’uso di uno strumento con scala graduata non correttamente (e. di taratura, in particolare e. di linearità), e si presenta sempre con lo stesso segno e con la stessa entità in tutte le misure; l’e. sistematico e un e. di cui si possono determinare le cause, rimuovendone pertanto gli effetti; si definisce accuratezza o giustezza la caratteristica di una misurazione o di uno strumento di essere affetti da piccoli e. sistematici; in altre parole l’e. sistematico fornisce l’entità dell’inaccuratezza (o ingiustezza) di una misurazione. L’e. accidentale deriva invece da tante cause che, pur se note, non sono quantificabili: per es., fluttuazioni di temperatura, di campo magnetico ecc. (e. dovuto a grandezze di influenza), giochi nelle parti mobili dello strumento (e. di mobilità) ecc.. L’e. accidentale e causa del fatto che le singole misure xi sono diverse tra loro; si definisce fedeltà (o anche ripetibilità o stabilità a seconda che ci si riferisca a prove di breve o lunga durata) la caratteristica di una misurazione o di uno strumento di essere affetti da piccoli e. accidentali. In altre parole l’e. accidentale fornisce l’entità dell’infedeltà di una misurazione; gli e. accidentali fluttuano nelle singole misure, assumendo con frequenze statisticamente eguali valori positivi o negativi. Va osservato che talvolta e. sistematici sono trattati come e. casuali, attribuendo a essi il massimo valore su tutto il campo di misura, come avviene, per es., per l’e. di linearità. Caratteristica risultante dall’accuratezza e dalla fedeltà e la precisione della misurazione o dello strumento; si può anche affermare che l’e. fornisce l’entità dell’imprecisione di una misurazione.

Quanto detto per una misurazione effettuata mediante uno strumento può essere ripetuto per un metodo di misurazione di una grandezza per il quale si appronta un’opportuna catena di misurazione. Eseguite n misure di grandezza X, se ne calcoli la media x̄= Ln i=1 xi/n. La media x̄ differisce dal valore vero x* a causa degli e. sistematici: infatti, se gli e. casuali assumono con frequenze statisticamente eguali valori positivi e negativi, non influenzano il valore della media; l’inaccuratezza di una misurazione o di un metodo di misurazione può essere determinata, per es., per confronto con un campione della grandezza. Se si eliminano, o, come avviene generalmente, si rendono trascurabili gli e. sistematici, e ragionevole assumere la media x̄ come valore più probabile di X; x̄ rende infatti minima la somma dei quadrati degli e. dando luogo a una compensazione degli e. (per il metodo dei minimi quadrati ➔ minimo) ; in tali condizioni si può valutare l’incertezza di una misurazione, o di un metodo di misurazione, con un’indagine a priori delle possibili cause di e. (lo strumento o il metodo sono in tal caso scatole aperte e se ne esamina dettagliatamente il funzionamento) oppure con un’indagine a posteriori consistente in un’elaborazione statistica di una serie di misure (lo strumento e in tal caso una scatola chiusa di cui si valuta la risposta). Il primo tipo di indagine interessa soprattutto il costruttore di uno strumento, o il metrologo che mette a punto un nuovo metodo di misurazione, i quali vogliono determinare la precisione dello strumento o del metodo; il secondo tipo di indagine interessa soprattutto l’utilizzatore di uno strumento, che vuole determinare l’attendibilità di una misura; tale tipo di indagine si basa sulla teoria degli e. di Gauss. Nel caso in cui la teoria degli e. di Gauss non sia applicabile, l’e. (e. massimo) può essere stimato calcolando la semidifferenza tra il massimo e il minimo valore ottenuti nella serie di misure.

2. Metodo d’indagine a priori

Si considerano separatamente tutti gli e. possibili che si possono commettere in una misura. Tali sono: l’e. di lettura, dovuto, in strumenti analogici, al limitato potere risolutivo dell’occhio, all’osservazione non corretta della posizione dell’indice (e. di parallasse), alle difficolta di interpolazione fra due tacche della graduazione; in strumenti digitali all’indeterminazione dell’ultima cifra (e. di troncamento); in entrambi i tipi di strumenti al rumore di fondo; l’e. di mobilità, dovuto ai giochi fra le parti mobili dello strumento; l’e. di isteresi, dovuto a fenomeni di isteresi meccanica in parti dello strumento che si deformano sotto carico (si pensi, per es., a un dinamometro a molla); l’e. provocato dalle grandezze di influenza, dovuto a fluttuazioni di temperatura, campo magnetico ecc., che, come accennato in precedenza, modificano in maniera casuale, imprevedibile, il funzionamento dello strumento; l’e. di zero (o di deriva) tipico di strumenti (o trasduttori), alcune caratteristiche dei quali variano nel tempo; l’e. di taratura, dovuto a imperfezioni della graduazione, al linearizzare leggi, scale ecc. che non sono lineari; l’e. provocato dalle grandezze di riferimento, dovuto all’uso di campioni imprecisi nel tarare lo strumento.

L’e. che si compie utilizzando lo strumento affetto dai suddetti e. possibili può essere assunto pari alla radice quadrata della somma dei quadrati degli e. possibili, per un criterio statistico in base al quale e estremamente improbabile che tutti gli e. possibili (accidentali) si presentino contemporaneamente e con il loro valore massimo. Ove non sia applicabile il criterio statistico di cui sopra, l’e. (e. massimo) può essere stimato calcolando la somma dei moduli dei singoli e. (massimi) possibili. Facendo il rapporto tra l’e. e il valore della grandezza misurata, si trova l’e. relativo che, nel caso in cui la grandezza sia pari alla portata massima dello strumento, ne definisce la classe di precisione (➔); l’incertezza della misura e pari, come detto, a 2ε e, come l’e., può essere rapportata al valore della grandezza ed espressa percentualmente.

3. Teoria degli e. di Gauss

fig.

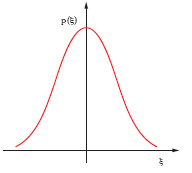
Mediante la teoria degli e. si può valutare a posteriori, statisticamente, l’e. di una misura: si calcoli la media delle misure effettuate e, detto ξi = xi G x̄ lo scarto della singola misura, si costruisca un istogramma con, in ascisse, gli scarti e, in ordinate, il numero di misure ni affette da scarto compreso in un intervallo di ampiezza Δξ; usando le frequenze νi = ni/n con cui si presentano gli scarti, resta immutata la forma dell’istogramma; se n e molto grande, al limite infinito, l’istogramma può essere approssimato con una curva continua (v. fig.) del tipo: y=(h/.‾‾‾ π)eGh2ξ2 (gaussiana; Gauss, Karl Friedrich), simmetrica rispetto all’asse delle ordinate, massima per ξ = 0, tendente a zero al tendere dello scarto a ±., sottendente un’area unitaria, e con h detto modulo di precisione; y fornisce una densità di frequenza in quanto, per ottenere la frequenza con cui uno scarto e compreso in un intervallo di ampiezza Δξ, occorre moltiplicarne il valore per Δξ; dalla densità di frequenza di uno scarto si passa allora alla densità di probabilità p(ξ) dello scarto stesso; pertanto la curva, detta curva di distribuzione degli scarti, fornisce in realtà la probabilità che uno scarto sia compreso fra ξ e ξ + Δ ξ o, in termini infinitesimi, fra ξ e ξ +d ξ; tale probabilità è pari a [1]

integrando in un intervallo finito [ξ1, ξ2], si ricava la probabilità che lo scarto di una misura sia compreso nell’intervallo stesso.

Passando ora all’errore εi, esso differisce dallo scarto corrispondente di una quantità costante Gε che, com’e immediato verificare, coincide con la media degli e. ed e pari alla differenza fra valor medio x̄ e valore vero x*, differenza quest’ultima dovuta agli e. sistematici. Se gli e. sistematici, in accordo con quanto detto precedentemente, sono trascurabili, Gε risulta molto piccolo, per cui, a meno di Gε, la curva di distribuzione degli e. coincide con quella di distribuzione degli scarti; pertanto la curva in figura (densità di probabilità p(ε) degli scarti) fornisce anche la probabilità p(ε) dε che l’e. di una misura sia compreso in un intervallo infinitesimo dε, probabilità che è pari a [2]

integrando in un intervallo finito [ε1, ε2], si ricava la probabilità che l’e. di una misura sia compreso nell’intervallo stesso. Quanto sopra e l’enunciato della legge degli e. o di Gauss. La p(ε) permette di legare il modulo di precisione h all’e. quadratico medio definito come [3] μ=.‾‾‾‾‾‾ Ln i=1 εi 2‾‾‾/‾n‾ ; si può dimostrare che [4] h=(μ/.‾‾‾ 2)G1 e pertanto e giustificato definire h modulo di precisione; infatti più piccolo e μ, cioè l’e. da cui mediamente (a parte il segno) e affetta una serie di misure, più è elevata la precisione con cui le misure stesse sono state eseguite. Si dimostra che per [5] p(ε) = ± μ la curva di distribuzione degli e. ha punti di flesso; si dimostra inoltre che la probabilità che un e. sia compreso tra Gμ e +μ e del 68,2%, ovvero che (confondendo valore medio e valor vero) e del 68,2% la probabilità che il valore di una misura xi sia compreso tra [6] x̄Gμ e x̄ + μ; analogamente si dimostra che la probabilità che ha un errore di essere compreso tra G2μ e +2μ e del 95,4%, tra G3μ e +3m e del 99,73%, e identiche sono le probabilità che il valore di una misura xi sia compreso rispettivamente tra x̄G2μ e x̄+2μ e tra x̄G3μ e x̄+3μ.

Oltre all’e. quadratico medio sono talora presi in esame: l’e. medio, definito come media dei moduli degli e., θ = Ln i=1 ∣εi∣/n; l’e. probabile, r, definito come l’e. tale che la probabilità di commettere un e. in modulo a esso superiore e 1/2. Se per la distribuzione degli e. vale la legge di Gauss, e: θ =.‾2‾/‾π‾ .μ=0,7979μ; r = 0,6745 μ. Il calcolo di μ, non essendo noti gli e. εi ma gli scarti ξi, può essere effettuato a partire da questi ultimi, attribuendo alla media degli e. Gε il valore μ/.‾n‾ cioè il valore dell’e. quadratico medio della media, più avanti definito; si dimostra che in tal caso μ=.‾‾‾‾‾‾ Ln i=1 ξi 2‾‾‾/‾(‾‾n‾‾G‾‾1‾‾) da cui la denominazione data all’e. quadratico medio di scarto tipo o deviazione standard. Si osservi come μ differisce dallo scarto quadratico medio, pari a .‾‾‾‾‾‾ Ln i=1 ξi ‾2‾‾/‾n‾ , per il fattore .‾n‾/‾(‾n‾‾G‾‾1‾); le due quantità coincidono per n molto elevato (in pratica > 30). Essendosi assunto x̄ come valore più probabile, e lecito chiedersi come valutare l’e. da cui e affetto x̄ supponendo di effettuare, sempre con le stesse modalità, m serie di n misure si avranno m medie x̄k di media x==Lm k=1 x̄k/m; al limite, per m molto grande, x= tende a x*; l’e. quadratico medio delle m medie, che pertanto e definito e. quadratico medio della media o e. standard, e pari, per il principio di propagazione degli e., a: σ = μ / .‾n‾ =.‾‾‾‾‾‾ Ln i=1 ξi 2‾‾‾/‾[‾‾n‾‾(‾‾n‾‾G‾‾‾1‾‾)‾] e per determinarlo basta una sola serie di n misure. L’e. standard può servire a determinare l’incertezza della misura effettuata: infatti la probabilità che la misura di X, cioè il suo valore vero x*, sia compreso tra x̄ Gσ e x̄ +σ e del 68,2%, la probabilità che x* sia compreso tra x̄ G2σ e x̄ +2σ e del 95,4%, tra x̄ G3σ e x̄ +3σ e del 99,73%; l’incertezza e quindi pari a 2σ con il 68,2% di probabilità, nel qual caso si scrive: x*= x̄±σ; si può assumere l’e. massimo pari a 3σ perché la probabilità è in tal caso uguale al 99,73% (quindi in pratica uno).

Nel caso in cui una stessa grandezza venga misurata con modalità e in condizioni diverse, per es. da osservatori diversi o con strumenti diversi, in modo da avere più serie di misure, a ciascuna di queste corrisponde in genere un differente e. quadratico medio, e quindi un differente modulo di precisione. In tal caso si assume la media pesata dei singoli valori medi come valore più probabile x0 della grandezza; i pesi delle singole medie devono essere inversamente proporzionali ai quadrati dei relativi e. quadratici medi, e quindi come pesi possono essere assunti i quadrati dei singoli moduli di precisione. Analoghe modifiche subisce l’espressione che fornisce l’e. standard.

4. Propagazione degli errori

Si supponga di determinare il valore di una grandezza Z dipendente da altre grandezze indipendenti Xj secondo la Z = Z(X1, X2, ..., Xj, ..., Xs), misurando separatamente le grandezze indipendenti: e questo, per es., il caso in cui si determina la velocita media di un corpo misurando separatamente lo spazio percorso e il tempo impiegato a percorrerlo; indipendentemente dal metodo con cui sono stati determinati gli e. delle Xj, nell’ipotesi che le singole misure delle varie grandezze siano distribuite secondo una gaussiana attorno al rispettivo valor medio x̄j (valore più probabile), l’e. quadratico medio μZ di Z e dato da [1] μZ = .GLGsG(GGG.GGZGGGG)GGG 2μ2X j j=1 .Xj che e appunto la legge di propagazione degli errori; nella [1] le derivate parziali (.Z/.Xj) sono calcolate in corrispondenza ai valori medi x̄j (e quindi al valore medio di Z) e μXj sono gli e. quadratici medi delle diverse grandezze. Se, per es., Z e la somma delle varie Xj, dalla [1] segue che l’e. quadratico medio e dato dalla radice quadrata della somma dei quadrati dei singoli e. quadratici medi. Se Z e data dal prodotto delle Xj, facendo riferimento all’e. relativo, quest’ultimo e pari alla radice quadrata della somma dei quadrati dei singoli e. relativi. Analogamente l’e. relativo di una radice n-esima e 1/n volte l’e. relativo del radicando. Applicando la [1] alla k-esima media xk=Ln i=1 xki/n, si trova l’e. standard: ogni misura e infatti affetta dallo stesso e. quadratico medio; si ribadisce come l’e. standard può essere determinato mediante una sola serie di n misure.

Quando non siano note le leggi di distribuzione delle singole misure, facendo riferimento agli e. massimi εX delle singole grandezze, la legge di propagazione degli e. si modifica nella [2] εZ = Ls ∣G.GZGG∣εXj j=1 .Xj ove εZ e l’e. massimo di Z. Utilizzando la [2] l’e. massimo di una somma e dato dalla somma degli e. massimi; analoghe modifiche (rispetto all’applicazione della [1]) subiscono gli e. massimi di un prodotto, di un quoziente, ecc. informatica Ogni tipo di malfunzionamento, durante l’esecuzione di un programma, di una procedura ecc., che non permette di ottenere il corretto raggiungimento del risultato aspettato.

I possibili e. vengono generalmente raggruppati in quattro categorie, che differiscono nelle cause e quindi nei metodi per la loro eliminazione: e. hardware, originati dal malfunzionamento di un qualche componente nella circuiteria del calcolatore o delle sue periferiche; per es., si può interrompere il circuito che memorizza il valore di un qualche bit e quindi l’informazione in essa contenuta può diventare erronea; e. software, generati da un’istruzione errata all’interno di qualche programma, non necessariamente in quello che ha prodotto i risultati sbagliati; e. di algoritmo, che si manifestano quando la procedura utilizzata per risolvere il problema e inadeguata in particolari circostanze; per es., la formula x=(Gb±.‾(‾b‾2‾‾G‾‾4‾‾a‾c‾)/2a, per trovare le soluzioni dell’equazione ax2+bx+c =0, e inadeguata quando a = 0 oppure b2G4ac < 0; e. di dati, prodotti dall’immissione di valori sbagliati, generalmente per un errore materiale dell’operatore, più raramente perché è stato ricevuto un carattere differente da quello trasmesso. Gli e. di dati vengono eliminati, o per lo meno ridotti, utilizzando per la trasmissione opportuni codici correttori di e. e controllando, per quanto possibile, la validità dei dati prima di farli utilizzare dal programma.

L’eliminazione degli e. software e di algoritmo fa parte della messa a punto (debug) del programma. La difficolta consiste nell’individuare i vari casi nei quali il programma fallisce e nel localizzare la o le istruzioni inadeguate; sara allora possibile modificarle in modo da trattare correttamente anche questi casi. Una volta eliminata una causa di errore software, la correzione e permanente e non soggetta a successiva usura; questo permette di affermare che la probabilità di esistenza di un e. in un programma e tanto minore quanto maggiore e il suo utilizzo. L’eliminazione degli errori hardware si ottiene localizzando e sostituendo il componente difettoso. Il problema della localizzazione del guasto può non essere banale, soprattutto quando questo si manifesti saltuariamente. I moderni calcolatori sono progettati in modo da tenere costantemente sotto controllo le proprie prestazioni e la corretta esecuzione di ogni operazione. Al manifestarsi di un e., l’elaborazione viene interrotta e il calcolatore cerca di identificare il tipo di e. e di individuare le possibili cause del guasto facilitando così i conseguenti interventi di manutenzione. Burst di e. Nella tecnica della trasmissione dati, gruppo di bit in cui la distanza tra due bit erronei consecutivi e minore di un prefissato l, intero positivo (lunghezza del burst); di conseguenza due bit erronei consecutivi apparterranno a burst differenti se risultano separati da almeno l bit esatti consecutivi. Codici rivelatori e correttori di e. Famiglie di codici (binari) nei quali l’introduzione di un’opportuna informazione ridondante permette di identificare la presenza di uno o più bit errati (codici rivelatori di e.) o addirittura di localizzare la posizione di eventuali bit erronei (codici correttori di e.). Il più semplice codice rivelatore di e. e realizzato aggiungendo, a ogni parola, un solo bit (bit di parità), il cui valore viene scelto in modo tale da rendere pari (codice a parità pari) o dispari (codice a parità dispari) il numero complessivo di bit con valore uno, nella parola codice risultante; è così possibile verificare la presenza di un bit erroneo semplicemente controllando che la parola presenti la stessa parità del codice cui appartiene. Questo codice e efficace solo quando sia praticamente trascurabile la probabilità di due errori simultanei nella stessa parola.

Per introdurre sistematicamente un maggior numero di bit di controllo, che permettono di rivelare la presenza di più errori nella stessa parola, si può ricorrere al metodo del controllo ciclico della ridondanza (cyclic redundancy check). In questo metodo gli n bit del messaggio da controllare vengono interpretati come i coefficienti di un polinomio di grado nG1: M(x)= LnG1 i=0 mixi; gli r bit di controllo (r < n) si introducono definendo un polinomio di grado r (detto appunto polinomio di controllo o polinomio generatore): G(x)= Lr i=0 gixi e realizzando, quindi, la codifica: W(x)=M(x).G(x). Per controllare la correttezza messaggio, si calcola W(x)/G(x)=Q(x)+R(x); se il resto della divisione, R(x), risulta eguale a zero, allora si interpreta il quoziente Q(x) come una copia fedele del messaggio M(x), se invece R(x)S 0, allora si riconosce la presenza di almeno un errore. Un polinomio generatore, particolarmente utilizzato nei sistemi di trasmissione dati sincroni, e G(x)=x16+x15+x2+1; il polinomio G(x)=x+1 si riduce al semplice controllo di parità. I codici correttori di e. sono costruiti, in generale, inserendo bit di parità che controllino determinate, e opportunamente scelte, posizioni dei bit della parola codice.