aerodinamica

Parte della meccanica che studia le leggi del moto dell’aria (o di un aeriforme qualsiasi) e dei corpi in essa immersi, con particolare riferimento ai problemi connessi al volo.

Generalità

L’aria, a seconda delle velocità in gioco, può comportarsi come un fluido incompressibile oppure compressibile: si parla, pertanto, di a. incompressibile e a. compressibile. Quest’ultima si suole qualificare, a seconda del valore della velocità, come a. subsonica, transonica, supersonica, ipersonica.

Il problema fondamentale dell’a. è quello della determinazione delle azioni dinamiche che l’aria esercita su un corpo in essa in moto. Tali azioni si valutano attraverso i cosiddetti ‘sforzi specifici’, o forze agenti sull’unità di superficie del corpo. In condizioni di quiete lo sforzo specifico è una pressione, un’azione cioè normale alla superficie su cui si esercita; altrettanto avviene in condizioni di moto in un fluido non viscoso. Se viceversa il fluido è viscoso, lo sforzo specifico avrà, oltre al componente normale, un componente tangenziale, proporzionale al coefficiente di viscosità del fluido e dipendente dall’orientamento dell’elemento di superficie che si considera e dalla velocità di deformazione del fluido. La determinazione degli sforzi specifici nei singoli punti d’una massa fluida in moto si deduce dall’integrazione di un sistema di equazioni differenziali che, sotto assegnate condizioni iniziali e al contorno, reggono il moto del fluido: il problema matematico generalmente è assai complesso ma si semplifica notevolmente trascurando la viscosità del fluido. Tuttavia ignorare la viscosità non è lecito, poiché essa, se pur minima, muta le condizioni di regolarità del moto del fluido, generando singolarità, essenzialmente di vortici formanti delle scie. A questi è dovuta la possibilità del volo, attraverso la nascita di resistenza e portanza, grazie alle quali un velivolo può sollevarsi da terra e tenersi in volo. La compressibilità dell’aria può essere trascurata per velocità subsoniche, cioè inferiori a quella del suono, mentre in regime transonico e ipersonico provoca radicali modificazioni delle azioni dinamiche che si esercitano su un profilo investito dalla corrente, generando in particolare onde d’urto.

A. incompressibile

fig. 1

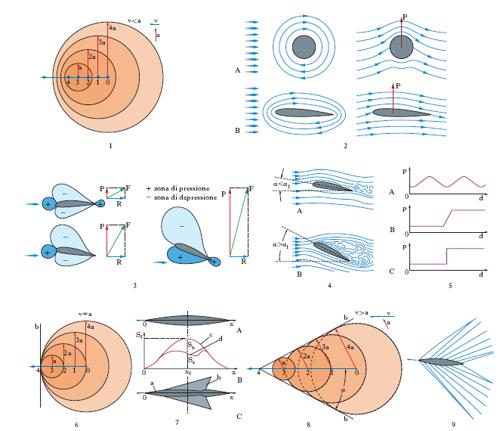
Alle basse velocità (non superiori a 120-150 m/s in aria), le variazioni della densità ρ del fluido per la presenza in esso di un corpo sono così piccole da poter considerare il fluido, anche se gassoso, come incompressibile. Se in un punto P di un fluido si produce una variazione della pressione p, e P è in quiete, tale perturbazione si propaga per onde sferiche con la velocità del suono a = √‾‾γp‾‾/ρ, ove γ è il rapporto fra i calori specifici del fluido, rispettivamente a pressione e a volume costante. Se invece P è dotato di velocità v 〈 a le onde che partono dalle posizioni successivamente occupate da P si possono addensare (fig. 1) come nell’effetto Doppler, influenzando la zona davanti al punto. Se la velocità del fluido nei singoli punti dello spazio, ovvero il campo delle velocità, non dipende dal tempo, pur potendo variare da punto a punto, si dice che il moto del fluido è stazionario e in tal caso le linee di corrente, cioè le traiettorie delle singole particelle del fluido, si identificano con le linee di flusso, cioè con le linee che hanno in ogni punto come direzione tangente quella della velocità del fluido. Fra le varie grandezze definibili nel campo cinetico, è importante la circuitazione C del vettore velocità v lungo una linea chiusa s: C risulta diversa da zero soltanto se il circuito è concatenato con vortici, se esso abbraccia cioè porzioni di fluido nel quale è rot v ≠0, ossia porzioni in cui vi sono particelle animate da velocità angolare non nulla. Se il moto è invece irrotazionale con rot v = 0 e il fluido è incompressibile con div v = 0, allora il campo di velocità si può far derivare da un potenziale Φ soddisfacente all’equazione di Laplace

δ²Φ δ²Φ δ²Φ

[1] Δ₂Φ = -- + -- + -- = 0.

δx² δy² δz²

Se in un fluido che occupi una regione indefinita è immerso un solido, il campo cinetico ha per contorno unicamente la superficie σ del solido. Il problema di determinare il potenziale Φ è risolubile quando su σ sia assegnato il valore di Φ (problema di Dirichlet) o il valore della sua derivata normale (problema di Neumann). In pratica, tuttavia, il problema si presenta spesso, per così dire, invertito, nel senso che, data una funzione Φ che soddisfa alla [1], si cerca quale è il corpo capace di determinare nel fluido un campo di velocità che ammetta Φ come potenziale. Così, per es., se la funzione Φ che soddisfa alla [1] rappresenta il potenziale di una corrente traslatoria uniforme in presenza di una singolarità costituita da un dipolo, si trova che il corpo è un cilindro di asse normale alla velocità v secondo x della corrente. Sulla superficie del cilindro con asse lungo z si determina in tal caso una distribuzione di velocità (e quindi di pressione) simmetrica rispetto ai piani xz e yz: in tali condizioni il corpo non riceve né dà alcuna spinta. In realtà, non essendo il fluido perfetto, i filetti fluidi si staccano a un certo punto dalla superficie del corpo, creando una scia: ne deriva una diversa distribuzione di pressioni, la cui risultante è la resistenza. Se cade l’ipotesi che la corrente sia puramente traslatoria e si ammette la presenza di vortici, il campo cinetico si modifica e con esso la forma del corpo, o almeno la distribuzione delle pressioni su di esso. Così, per es., se ferme restando le condizioni precedentemente accennate si ammette altresì la presenza di un vortice rettilineo e indefinito, il corpo è ancora un cilindro, ma la distribuzione delle pressioni su di esso, simmetrica rispetto al piano xz, non lo è più rispetto a yz: nasce, com’è provato dall’effetto Magnus, una portanza. Effetti di portanza nascono anche se, in luogo di un vortice rettilineo e indefinito, si ipotizza una serie di vortici distribuiti lungo l’asse x; il potenziale risultante è tale che la soluzione è quella di un corpo affusolato nel senso dell’asse x, cioè nel verso di avanzamento della corrente: corpi di questo genere furono studiati per i dirigibili. Sin dai primordi dell’aeronautica, peraltro, seguendo gli esempi forniti dalla natura, la portanza è stata ottenuta non mediante corpi estesi, ma superfici, prima piane (donde il nome di aeroplano) poi curve: le ali. Poiché intorno alla sezione di un’ala (profilo alare) si instaura un flusso circolatorio, essa è rappresentabile mediante un vortice. Così, sotto quest’aspetto, si stabilisce un’equivalenza tra un cilindro nelle condizioni sopra indicate e un profilo alare: la sovrapposizione dei due campi di velocità, traslatorio e di rotazione intorno al cilindro (fig. 2A), traslatorio e di circolazione intorno all’ala (fig. 2B), dà luogo alla portanza P. I profili alari sono disegnati in modo che vi sia una differenza di velocità, rispetto all’ala, tra gli strati d’aria che scorrono rispettivamente lungo la superficie superiore e inferiore del profilo; la velocità è maggiore lungo la parte superiore del profilo e quindi, in accordo con il teorema di Bernoulli, la pressione esercitata dall’aria sulla superficie superiore dell’ala è minore rispetto a quella esercitata sulla superficie inferiore: la differenza di pressione contribuisce alla portanza, ma non ne è l’unica causa. L’ala infatti è disegnata e disposta così che l’aria che scorre lungo di essa sia deviata verso il basso generando sull’ala, per la terza legge di Newton, una spinta verso l’alto. Le linee di corrente dorsali e ventrali non si richiudono, ma formano la scia, che cresce al crescere dell’angolo d’incidenza (o incidenza) α del profilo. La fig. 3 riporta, per tre diversi angoli d’incidenza, la distribuzione delle pressioni che si riscontrano in un profilo alare e la risultante F delle forze dovute alle pressioni stesse, di componenti P (portanza) e R (resistenza). Superato un determinato valore dell’angolo d’incidenza, detto critico (α₁ compreso tra 12° e 18° a seconda del profilo), i filetti non riescono più a seguire il dorso alare, come accade per valori minori di α₁ (fig. 4A), e così si determina una forte scia e una brusca caduta della depressione dorsale e quindi della portanza (distacco di vena o stallo: fig. 4B).

A. compressibile
Subsonica e transonica

Nel campo di velocità compreso tra ca. 0,4 e 1,2 M (ove M è il cosiddetto numero di Mach legato alla velocità del suono nel fluido dalla relazione M = v/a), l’equazione del potenziale è un’equazione a derivate parziali del secondo ordine non lineare, come la [1], in quanto i coefficienti contengono le incognite. La si può linearizzare con il metodo delle perturbazioni, ammettendo cioè che le velocità incrementali provocate dal corpo nella corrente siano molto piccole rispetto a v e ad a. L’equazione si semplifica così nella

δ²Φ δ²Φ δ²Φ

(1-M²) -- + -- + -- = 0

δx² δy² δz²

che però non è valida nel campo transonico né in quello ipersonico. A partire da un certo numero di Mach critico, si verifica la cosiddetta crisi di compressibilità, con la corrispondente comparsa di un’onda d’urto sul dorso del profilo: in corrispondenza della zona di massima depressione si forma una piccola regione a velocità supersonica, mentre su tutti gli altri punti del corpo la velocità resta subsonica. Aumentando la velocità v, la zona supersonica si estende e l’onda si sposta a valle, fino al formarsi di un’altra onda, che prima tende a spostarsi a monte, sino a interferire con la prima, poi se ne separa; e infine nasce un’onda ventrale a valle. Dietro la prima delle onde d’urto la corrente si stacca dal corpo, ciò che dà origine a una forte resistenza, che si aggiunge a quella, detta resistenza d’onda, connessa con la dissipazione d’energia dovuta all’aumento di entropia che si verifica nel fluido. Infig. 5 è schematicamente mostrato l’andamento della pressione p in funzione della distanza d percorsa da un’onda acustica (A), da un’onda d’urto reale (B) e quello che risulta dalla teoria (C). L’andamento della temperatura e della densità è analogo. Quando la velocità v raggiunge nella zona indisturbata un valore pari ad a (M=1), si crea la situazione schematicamente mostrata nella fig. 6 (b è il fronte d’urto normale). L’insorgere della crisi di compressibilità può ritardarsi usando profili in cui lo spessore massimo sia spostato verso il bordo di uscita o che abbiano una parte dorsale molto pianeggiante; inoltre conviene che il bordo dell’ala formi un certo angolo ϕ col piano normale alla velocità (ala a freccia), così che soltanto la componente v cos ϕ influisca sulla distribuzione di pressione (mentre la componente v sen ϕ dà luogo unicamente ad azioni lungo l’apertura alare): l’esperienza dimostra che in tal mo;do il numero di Mach critico aumenta con √‾‾‾‾‾‾sec ϕ (anziché con sec ϕ). Ciò che si verifica per le ali si verifica, seppure in misura assai più ridotta, per i corpi affusolati. Particolare menzione però occorre fare degli insiemi di ali e corpi affusolati, negli aeroplani per es., per l’importanza che assume l’interferenza reciproca in regime transonico. Vale in tal caso la regola delle aree: la resistenza d’onda in corrente transonica o debolmente supersonica è uguale a quella di un corpo di rivoluzione di uguale lunghezza lungo l’asse, che presenti la stessa legge di variazione dell’area delle sezioni trasversali dell’insieme. In pratica, trovata la forma di minima resistenza del fuso di rivoluzione (fig. 7A), si diminuisce, in ogni piano normale alla velocità di volo v (per es. quello corrispondente a x₁ in fig. 7B), l’area S_f della sezione del fuso di una quantità uguale all’area S_b della sezione, con il medesimo piano, dell’ala b o della coda, sino ad avere l’area S_a della corrispondente sezione della fusoliera a. In tal modo la fusoliera presenta, in corrispondenza della parte interessata dall’ala e dalla coda, un caratteristico restringimento (fusoliera a vita di vespa; fig. 7C): in tale zona si ha un campo d’espansione che attenua l’onda d’urto.

Supersonica

È quella relativa a numeri di Mach tra ca. 1,2 e 5. La situazione che si determina per il generico punto P è illustrata nella fig. 8: P si muove davanti a onde che risultano comprese entro un cono di semiapertura μ = arcsen a/v, sulla cui superficie si vanno a trovare le perturbazioni nascenti dal deflusso della corrente sulla superficie del corpo in P (b nella fig. 8). Se la parete presenta vari spigoli salienti, in corrispondenza di ciascuno di essi si formeranno varie onde d’urto sempre meno o sempre più inclinate, secondo che nei vari punti la superficie sia concava o convessa. Se la corrente investe un corpo acuminato, l’onda d’urto si accosta al corpo; se investe un corpo arrotondato, l’onda d’urto resta staccata, lasciando dietro a essa una zona subsonica. Quando due onde d’urto sono prodotte da due deviazioni successive di una stessa parete, esse convergono fondendosi e dando luogo a un’unica onda più violenta; quando un’onda d’urto interferisce con linee d’espansione, si ha un indebolimento di essa e un incurvamento (fig. 9). Studiando la corrente supersonica attorno a diversi modelli, si trova, in particolare, che una parte della resistenza d’onda dipende dalla forma del profilo, l’altra (resistenza d’onda indotta) dal quadrato dell’incidenza. Le esperienze forniscono resistenza un po’ maggiore e inclinazione della retta della portanza un po’ minore di quelle teoriche, per la presenza rispettivamente della resistenza di attrito e dell’effetto dello strato limite (strato di fluido in cui la velocità è variabile da 0 a v). Se il bordo d’attacco dell’ala è inclinato di un certo angolo ϕ, vale quanto già detto nel caso transonico. Se ϕ 〈 90° − μ, cioè se è M_n >1, con M_n il numero di Mach normale, l’ala è a bordo d’attacco supersonico (bordo davanti al cono di Mach); se ϕ > 90° − μ, cioè se M_n 〈 1, l’ala è a bordo d’attacco subsonico, e si applicano le formule dell’a. subsonica.

Ipersonica

Il limite tra l’a. supersonica e quella ipersonica è piuttosto convenzionale, poiché, a seconda della forma del corpo, caratteri ipersonici della corrente possono aversi per numeri di Mach, M, anche non molto elevati; comunque si ammette in genere che si abbiano velocità ipersoniche per M > 5. A numeri di Mach ipersonici nascono nuovi fenomeni fisici e chimici dovuti alle alte temperature che si hanno dietro le onde d’urto e nello strato limite. La necessità di ridurre al minimo gli effetti del riscaldamento aerodinamico (o cinetico) del veicolo esige l’adozione di forme tozze sia per le ali sia per la fusoliera; ne seguono, alle velocità ipersoniche, campi di velocità, attorno al veicolo, di tipo transonico, con conseguenti serie complicazioni di calcolo. Inoltre, in campo altamente supersonico e in campo ipersonico, comincia a essere sempre più sensibile, a causa della temperatura, l’effetto dei moti vibratori delle molecole, di ampiezza crescente con il crescere della temperatura: l’energia comunicata al gas viene assorbita in parte da questo grado di libertà elastico, in parte da elettroni che si eccitano. Al crescere della temperatura, per effetto degli urti reciproci, le molecole cominciano a dissociarsi; la dissociazione è favorita anche dalle basse pressioni e varia quindi, per un dato veicolo, con la quota e con la velocità. Al crescere ulteriore della temperatura comincia a prodursi la ionizzazione per urto termico sia delle molecole sia degli atomi; gli elettroni liberati acquistano velocità elevatissime; cresce via via la concentrazione degli ioni positivi e degli elettroni, e il gas tende a trasformarsi in plasma. I fenomeni cui si è ora accennato avvengono con assorbimento di energia. Le particelle del gas rallentano urtando quelle meno veloci, già frenate a causa della presenza del solido: la loro energia cinetica si trasforma in energia termica, nei gradi di libertà di rotazione e di vibrazione, e per la dissociazione e la ionizzazione. Naturalmente è necessario un certo tempo (sia pure molto piccolo) perché la trasformazione possa avvenire, cioè perché le particelle, urtandosi tra loro, possano perdere lo stato fisico-chimico primitivo per acquistare il nuovo; questo tempo è legato al cammino libero medio. Nelle onde d’urto, per es., il cambiamento delle caratteristiche fisiche del gas avviene lungo lo spessore finito dell’onda, spessore che è dell’ordine di diversi cammini liberi medi. Si intuisce che alle quote elevate, cioè con cammino libero medio sufficientemente grande e alte velocità, i ritardi o i tempi di rilassamento siano lunghi rispetto alle condizioni di equilibrio. A valle di onde d’urto intense l’equilibrio è raggiunto quasi istantaneamente; al contrario, lungo una parete piana impermeabile al calore il rilassamento è molto più lento e lo stato di non equilibrio iniziale può persistere a lungo (deflusso congelato). Metodi approssimati sono stati ideati, con riferimento a corpi tozzi, per il tracciamento della linea sonica entro lo strato d’urto al variare del numero di Mach della corrente; la linea sonica separa la regione centrale subsonica dalla restante supersonica; per corpi con superficie a curvatura costante la posizione della linea sonica varierebbe poco con M e con le caratteristiche del gas. Alle velocità ipersoniche la rilevante decelerazione della corrente provocata dalle onde d’urto e dalla viscosità fa aumentare molto la temperatura del fluido; necessariamente, a parità di numero di Reynolds, lo spessore dello strato limite cresce, si esaltano i fenomeni di vibrazione, dissociazione e ionizzazione, di diffusione di atomi e ioni di varia specie, e anche i fenomeni di ricombinazione. L’aumento dello spessore dello strato limite equivale, sostanzialmente, ai fini del deflusso, a una variazione della forma del solido e provoca la comparsa di altre onde d’urto; interferenze si hanno inoltre tra vorticità dello strato limite e vorticità dello strato d’urto dovute alla forte curvatura dell’onda d’urto. Agli effetti viscosi è strettamente connessa la trasmissione del calore dal fluido al solido per convezione forzata. Alla trasmissione per convezione bisogna aggiungere la trasmissione per irraggiamento, che però nell’atmosfera terrestre è piccola rispetto a quella per convezione forzata.