idrodinamica
Parte dell’idraulica che studia i problemi di moto dei liquidi.
Leggi dell’i. per un liquido non viscoso
Si assume come ipotesi fondamentale che il liquido considerato sia privo di viscosità, cioè esente da attrito interno; tale ipotesi si traduce nel fatto che nel generico punto P della massa liquida, lo sforzo (➔) specifico su un qualunque elemento dσ di superficie per P è normale a dσ ed è sempre una pressione. Questa, o per via teorica (osservazione di Cauchy) o per via sperimentale (principio di Pascal), si dimostra indipendente dall’orientamento dell’elemento (potendo però variare da punto a punto) di modo che qualunque sia dσ, il risultante di tutte le azioni molecolari che le particelle di liquido poste da una parte (faccia negativa) di dσ esercitano sulle particelle contigue poste dall’altra (faccia positiva) si può porre nella forma pndσ, essendo p > 0 e n essendo il versore della normale a dσ orientata dalla sua faccia negativa verso la sua faccia positiva. In modo analogo si può definire la pressione che un liquido esercita sulla parete del recipiente che lo contiene, assumendo in questo caso per dσ un elemento della parete medesima.
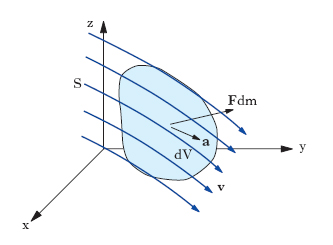
L’i. può essere sviluppata secondo il punto di vista euleriano o secondo il punto di vista lagrangiano; il punto di vista euleriano, che è generalmente, per le applicazioni tecniche, il più conveniente, consiste nel considerare la vicenda del moto punto per punto del campo S in cui esso si svolge (e non particella per particella della massa liquida, come si fa quando si riguardano le cose dal punto di vista lagrangiano). Da questo punto di vista il problema dinamico si potrà considerare risolto quando, note le forze agenti sulla massa e al contorno, si riesca a determinare in funzione del posto, cioè in funzione delle coordinate x, y, z, e in funzione del tempo, la velocità v, la pressione p, la densità ρ. Si supponga che un elemento liquido infinitesimo, di volume dV e massa dm = ρdV (fig. 1), sia soggetto a una forza Fdm (F è la forza agente sull’unità di massa); applicando i principi della dinamica si stabilisce innanzitutto la cosiddetta equazione vettoriale indefinita, valida cioè punto per punto, che, per un qualunque fluido non viscoso, si può porre nella forma
[1] ρa = ρF − grad p.
Alla [1] va associata un’altra equazione, scalare, indefinita: la cosiddetta equazione di continuità, che traduce in forma matematica il principio fisico della conservazione della massa e che, sempre in forma euleriana, si può scrivere
∂ρ
[2] div (ρv) + −−−− = 0.
∂t
Le equazioni scalari che si hanno a disposizione sono in totale 4 (3 corrispondenti all’equazione vettoriale [1] e la [2]), mentre le incognite, pure scalari, sono 5 (le 3 componenti della velocità, p e ρ); una quinta equazione è fornita da una relazione, equazione caratteristica o di stato, suggerita da considerazioni di natura termodinamica, caratteristica della sostanza in esame, che lega fra loro, in generale, pressione, densità e temperatura. L’aggiunta di una quinta equazione sembra introdurre una nuova incognita, la temperatura: in realtà in molti casi di notevole interesse (liquidi omogenei, gas perfetto in condizioni isotermiche o adiabatiche ecc.) l’equazione di stato si riduce a una relazione fra pressione e densità soltanto, cioè è del tipo
[3] ρ = f(p)
permettendo di introdurre la funzione, della sola pressione,
dp
[4] P = ∫−−−,
ρ
e di scrivere quindi la [1] nella forma
[5] a = F − grad P.
La grandezza P definita dalla [4] ha le dimensioni del rapporto fra un’energia e una massa e viene spesso indicata col nome di energia idrodinamica interna. In particolare per un fluido incompressibile (in particolare per un liquido omogeneo, quale si può generalmente considerare l’acqua) la [3] e la [4] si riducono rispettivamente a
[6] ρ = cost = ρ0,
p
[7] P = −−−,
ρ0
essendo ρ0 il valore della densità in un prefissato stato di riferimento del sistema; simultaneamente, in dipendenza della sola ipotesi di incompressibilità, l’equazione di continuità si riduce a
[8] div v = 0.
Se, come si verifica in casi di notevole importanza, le forze di massa sono conservative, con potenziale U, la [5] si può porre nella forma
[9] a = grad (U − P).
L’integrazione del sistema delle 5 equazioni differenziali indicate nelle 5 funzioni incognite richiede che siano altresì fissate le condizioni iniziali (valori che all’istante iniziale t0 competono a tutte e 5 le funzioni incognite in tutti i punti del campo) e le condizioni al contorno (stato di quiete o di moto in cui si trovano le pareti o i fluidi con i quali il liquido considerato è a contatto). Ove l’integrazione non risulti effettuabile per via analitica, si può ricorrere a metodi di calcolo numerico.
Una prima semplificazione del problema, dovuta a Lagrange, si ha se si può ammettere che esista una funzione ϕ (x, y, z, t) tale che le componenti u, v, w della velocità siano le derivate parziali di ϕ rispetto a x, y, z:
∂ϕ ∂ϕ ∂ϕ
[10] u = −−−−, v = −−−−, w = −−−−,
∂x ∂y ∂z
cioè se il campo v delle velocità deriva da un potenziale ϕ, nel qual caso si parla di moto irrotazionale (gli spostamenti delle particelle risultano esenti da rotazione). In un liquido non viscoso, ammesso che ρ dipenda solo da p, all’esistenza di un potenziale di velocità segue necessariamente quella di un potenziale U delle forze di massa, in modo che l’equazione fondamentale va assunta nella forma [9]. D’altra parte, se esiste un potenziale ϕ della velocità, le componenti dell’accelerazione vengono a coincidere con le derivate parziali della funzione
∂ϕ v2
−−−− + −−−−,
∂t 2
cioè si ha
∂ϕ v2
[11] a = grad (−−−− + −−−−),
∂t 2
e l’equazione vettoriale [9] si riduce in definitiva alla unica equazione scalare
∂ϕ v2
[12] −−−− + −−−− − U + P = C,
∂t 2
dove C è una funzione arbitraria dipendente soltanto dal tempo, che non è possibile precisare se non caso per caso in base alla natura del problema che si tratta. Resta così fra l’altro stabilito che, per i moti irrotazionali, le 5 equazioni, con altrettante incognite, del caso generale, si riducono a 2 (la [12] e l’equazione di continuità) nelle incognite P e ϕ. L’equazione di continuità a sua volta, nell’ipotesi di irrotazionalità del moto, per un fluido incompressibile, per il quale in generale si presenta nella forma [8], si trasforma nella
∂2ϕ ∂2ϕ ∂2ϕ
[13] ∇2ϕ = −−−− + −−−− + −−−− = 0,
∂x2 ∂y2 ∂z2
ciò che vale anche a mettere in evidenza il carattere di funzione armonica che ha in tali casi il potenziale di velocità.
Altre semplificazioni, indipendentemente dall’ipotesi di irrotazionalità, si hanno allorché, essendo il fluido non viscoso e soggetto a sollecitazione conservativa, si possa considerare raggiunto un regime stazionario, cioè condizioni di moto in cui le diverse grandezze in gioco, pur potendo ancora eventualmente variare da posto a posto, risultino indipendenti dal tempo. In tal caso, che si presenta in notevoli problemi di interesse tecnico, le traiettorie delle singole particelle, linee di corrente, coincidono con le cosiddette linee di flusso, cioè con le linee del campo del vettore velocità; l’equazione di continuità si riduce a
[14] div (ρv) = 0,
e la [9] si può interpretare, analogamente, come l’equazione del moto di un punto in un campo di forza stazionario il cui potenziale unitario è U−P, onde vale l’integrale delle forze vive che si traduce nella
v2
[15] −−−− − U + P = costante,
2
la costante potendo in generale variare da una linea di flusso all’altra. Il risultato, che può considerarsi come uno dei teoremi fondamentali dell’idraulica, dovuto a D. Bernoulli, si può esprimere dicendo che lungo ogni linea di flusso si mantiene costante, riferita all’unità di massa, la somma dell’energia cinetica v2/2, dell’energia potenziale −U e dell’energia interna P. Se poi si aggiunge a quella della stazionarietà del moto l’ipotesi che esso sia anche irrotazionale, come subito si ricava dalla [12], la relazione [15] sussiste con un unico valore della costante in tutto il campo sede del moto e viene talora indicata come integrale di Lagrange. Per i liquidi omogenei, P=p/ρ e si ha
v2 p
[15′] −−−− − U + −−−− = costante.
2 ρg
Se, in particolare, le forze di massa si riducono al peso, ciò che, assunta come asse z la verticale ascendente, implica U=−gz, la [15′] si riduce a
v2 p
[16] −−−− + z + −−−− = costante.
2g ρg
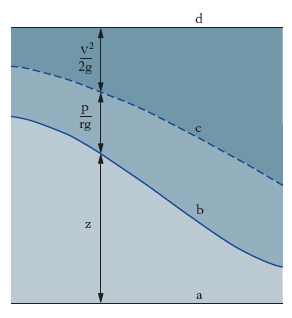
Il termine v2/(2g), che ha come gli altri due le dimensioni di una lunghezza, dà l’altezza dalla quale deve cadere, nel vuoto, un grave inizialmente in riposo per acquistare la velocità v, e ha perciò il nome di altezza o quota cinetica, ovvero anche di altezza d’arresto (in quanto dà l’altezza alla quale giungerebbe un grave lanciato, nel vuoto, verticalmente verso l’alto con velocità v); il secondo termine è la effettiva quota verticale del posto P che si considera e si chiama altezza effettiva o geometrica; il terzo, detto altezza piezometrica, rappresenta l’altezza, sopra il punto P, di una colonna liquida capace di produrre col suo peso la pressione p. Così, la [16], esprimibile graficamente come in fig. 2, si può enunciare dicendo che in ogni punto di un liquido omogeneo, pesante, animato da un moto irrotazionale, stazionario, la somma delle tre quote (geometrica, d’arresto e piezometrica) ha sempre lo stesso valore.
Come immediata conseguenza della [16] si può stabilire il teorema di Torricelli: la velocità con cui le particelle di un liquido pesante effluiscono, in condizioni di moto irrotazionale, da un piccolo orifizio praticato nella parete di un recipiente dove il liquido sia mantenuto a livello costante (di modo che il regime di efflusso risulti stazionario) è quella stessa che corrisponderebbe alla caduta libera di un grave dal livello della superficie libera del liquido, cioè è uguale a √‾‾‾‾2gh, essendo h il battente o carico (differenza di livello fra orifizio e pelo libero).
Linee idrodinamiche
Su una superficie topografica, sono le traiettorie di punti materiali che, partendo dalla quiete, si muovono sotto la sola azione della gravità, e secondo le quali defluirebbe quindi l’acqua se potesse scorrere sulla superficie senza attrito. Generalmente non coincidono con le linee di massima pendenza della superficie: si ha tale coincidenza soltanto quando le linee di massima pendenza sono contenute in piani verticali. In pratica però i due sistemi di linee non differiscono molto nel loro andamento generale.