topografia
Geografia
La disciplina che studia le relazioni che si possono stabilire, sulla base di modelli teorici, tra l’insieme finito di coordinate di punti e quello di grandezze misurabili; affronta poi le problematiche connesse alla realizzazione dei modelli stessi. Le applicazioni topografiche, per la massima parte, sono quindi finalizzate ad attribuire valori numerici a coordinate di punti sottoposti a osservazione.
Rilievo e tracciamento
Le fondamentali operazioni topografiche sono il rilievo e il tracciamento. Con il rilievo di una zona della superficie terrestre, si inseriscono punti della zona stessa in un prefissato sistema di coordinate e cioè si attribuiscono a tali punti coordinate riferite a quel dato sistema. Nella fase iniziale, di ricognizione, si scelgono punti che, al meglio, schematizzino la morfologia locale, tenute presenti le finalità del rilievo; si passa poi a ‘collegare’ i punti mediante operazioni di misure topografiche secondo schemi geometrici che la t. propone; si elaborano infine i dati, ottenendo i valori incogniti delle coordinate dai quali si trae, nel caso in considerazione, la ‘carta’ della zona (➔ carta).
Nel tracciamento si parte, invece, da coordinate note di punti dalle quali si deducono valori numerici per le grandezze misurabili, per es., distanze, angoli ecc. che si prevede intervengano nella fase esecutiva. Anche questa operazione viene condotta con finalità diverse, tra le quali il riporto sul terreno di punti di opere progettate e in fase di realizzazione. Si parte dalla scelta di punti dell’opera, significativi nei riguardi del tracciamento e dei quali si suppongono note le coordinate di progetto: si tratta di ‘riportare’ sul terreno i punti stessi, cioè di trovare nella zona interessata dal lavoro, i punti corrispondenti a quelli di progetto considerati; la t. interviene con schemi operativi idonei, definiti dagli elementi misurabili in precedenza calcolati.
Particolare menzione meritano, tra le applicazioni della t., le misure di deformazione che hanno lo scopo di determinare, in grandezza, direzione e verso, deformazioni elastiche o permanenti subite da determinati sistemi sotto l’azione di forze interne e/o esterne. Tale applicazione va a interessare operazioni di collaudi di strutture, studi di movimenti franosi e, in generale, i fenomeni di movimento che possano prevedersi lenti relativamente ai tempi di osservazione; si scelgono opportuni punti dell’‘oggetto’ che vengono rilevati topograficamente in un momento iniziale; mantenendo il più possibile le modalità del rilievo, si osservano in epoca successiva gli stessi punti; il confronto delle coordinate calcolate alle diverse epoche consente di stimare i parametri della deformazione. Il campo d’intervento della t. nelle più comuni applicazioni dell’ingegneria civile è dunque ampio: in fase di progetto, la t. è in grado di dare informazioni sulla stabilità e sulla morfologia della zona interessata; in fase esecutiva assicura il fedele riporto sul terreno di particolarità progettuali; nelle fasi di collaudo e monitoraggio concorre, infine, a valutare la rispondenza dell’opera rispetto ai dati teorici di calcolo e la sua stabilità nel tempo.
Gli strumenti classici impiegati per i rilievi t. sono di tipo e d’impiego assai vario. Vi rientrano sia gli strumenti atti ad alcune operazioni elementari di rilievo, quali il filo a piombo, la fettuccia e la rotella metrica, la diottra, la livella, gli squadri, sia strumenti ottici ed elettronici di caratteristiche diverse: distanziometri, livelli teodoliti, aventi spesso elevatissimo grado di precisione.
Determinazione planimetrica e altimetrica
I problemi topografici sono riconducibili, per la massima parte, a problemi di determinazione della posizione di punti nello spazio. Il modello funzionale, conseguentemente, dovrebbe risultare un modello tridimensionale, tendenza sollecitata soprattutto dal ricorso ormai generalizzato a rilievi con utilizzo di satelliti artificiali. Non va per questo abbandonata la concezione classica del problema che introduce superfici di riferimento e scinde il problema del posizionamento dei punti in due operazioni, almeno concettualmente, distinte e consistenti, la prima, nella determinazione bidimensionale planimetrica sulla superficie adottata, la seconda, nella determinazione unidimensionale altimetrica con riferimento alla stessa o ad altra superficie.
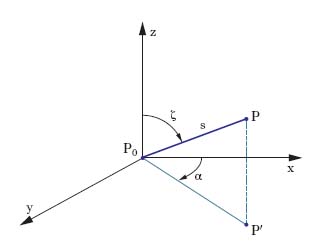
La t., secondo la concezione classica, opera in campi relativamente molto ristretti e come superficie di riferimento adotta il piano tangente alla superficie di livello in un punto centrale P0 della zona considerata, e in esso il riferimento (P0, x, y) con scelta opportuna degli assi orientati x, y. L’asse z, normale al piano, è diretto verso lo zenit di P0. In questo sistema locale un punto viene fissato mediante l’angolo azimutale α, il segmento spaziale s e l’angolo zenitale ζ (fig. 1); nel caso di determinazione separata planimetrica e altimetrica, a definire il punto sono l’angolo azimutale, α, il segmento nel piano, P0P′, e l’altezza di P sul piano per z. Tale modello si può accettare in un intorno di P0 limitato e legato alla morfologia del terreno e alla finalità del lavoro: ma via via che ci si allontana da P0 la curvatura terrestre fa sentire i suoi effetti e il modello adottato non è più rispondente.
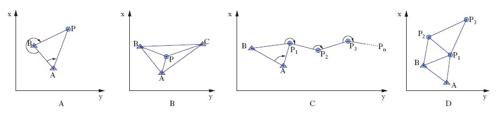
Nel modello piano, quindi, i dati sono elaborati secondo algoritmi della geometria piana euclidea e della trigonometria piana. Le relazioni tra grandezze misurabili e coordinate vengono dalla considerazione di schemi geometrici molto semplici, i quali possono essere finalizzati alla determinazione di punti singoli, punti in successione, punti distribuiti. Le grandezze misurabili sono distanze, angoli azimutali (orizzontali) e verticali; tali grandezze definiscono schemi geometrici piani che vengono introdotti come isodeterminati, contenenti cioè un numero di elementi misurabili strettamente necessario. L’inserimento nel sistema di coordinate viene effettuato imponendo condizioni che si traducono essenzialmente nell’appoggio a punti noti o ‘fissi’. Tra le metodologie di rilievo di punti singoli le principali sono quella per coordinate polari e quella per intersezione. La prima è largamente seguita, specialmente per rilievi di dettaglio: dati due punti d’appoggio A e B noti, si fa stazione in uno di essi e con orientamento all’altro, si misura la direzione al punto ‘nuovo’ P e la sua distanza (spaziale) dalla stazione (fig. 2A); la misura dell’angolo zenitale consente la riduzione all’orizzonte di stazione della distanza e, se richiesta, la determinazione del dislivello punto stazione-punto nuovo. La seconda prevede, nel caso di intersezione semplice in avanti, la misura degli angoli di base del triangolo formato da due punti noti, in cui si fa stazione, e dal terzo nuovo punto P; nell’intersezione inversa, nota anche come problema di Snellius o di Pothenot, si misurano, con vertice nel punto nuovo, P, gli angoli compresi fra le direzioni con tre punti fissi A, B, C; nell’intersezione lineare si misurano i lati del triangolo definito dai due punti fissi e dal punto nuovo (fig. 2B). Per determinare punti in successione, si rilevano percorsi poligonali che formano una spezzata che collega punti fissi e nuovi: in corrispondenza dei vertici si misurano i lati e gli angoli tra le direzioni in essi concorrenti. Due punti noti A e B consentono l’inserimento del rilievo nel sistema che i punti stessi definiscono (fig. 2C). Per punti distribuiti si formano reti (➔ triangolazione) collegando i punti stessi in figure triangolari (fig. 2D). Si distinguono reti triangolate, trilaterate e miste in base al tipo di misure previste.
Le determinazioni altimetriche sono volte ad attribuire valore numerico alla terza coordinata, comunemente intesa come quota del punto. È necessario osservare che la definizione di quota non è unica: per es., si parla di quota ellissoidica per indicare la distanza spaziale tra il punto P della superficie terrestre e il piede della perpendicolare per P all’ellissoide; di quota ortometrica per indicare la lunghezza dell’arco di linea di forza del campo della gravità compreso tra P e l’intersezione della linea con il geoide (➔); di quota dinamica, se la si collega alla differenza di potenziale tra P e un punto qualsiasi del geoide.
Principali procedimenti di misura
Le misure topografiche definiscono dislivelli il cui significato fisico e geometrico è legato alla metodologia adottata nella misura. I due procedimenti di misura principalmente seguiti sono la livellazione geometrica e la livellazione trigonometrica (➔ livellazione). La livellazione geometrica prevede metodologie operative e strumentazioni strettamente legate alle precisioni che si vogliono conseguire; per es., nel caso della ‘livellazione del mezzo’ si suddivide la linea da livellare in tratti di lunghezza non superiore a 100 m: agli estremi di ciascun tratto sono poste, verticali, due stadie e in posizione equidistante da esse un livello. Il dislivello parziale è dato dalla differenza tra i valori letti sulla stadia nel punto iniziale (battuta indietro) e sulla stadia nel punto finale (battuta avanti); il dislivello tra gli estremi della linea è dato dalla somma dei dislivelli parziali. Nel caso di apprezzabili variazioni gravimetriche, vanno apportate le opportune correzioni al fine di dedurne quote come sopra definite. Con la livellazione trigonometrica si vogliono determinare dislivelli ellissoidici; si ipotizza un modello semplice dell’atmosfera in base al quale descrivere i fenomeni collegati alla propagazione di raggi luminosi o, più in generale, di onde elettromagnetiche. Si può così considerare uno schema operativo semplice, che prevede la misura della distanza tra i punti da livellare e dell’angolo zenitale in uno di essi (livellazione da un estremo) o della distanza e degli angoli zenitali misurati contemporaneamente in entrambi i punti (livellazione reciproca dagli estremi).
Si distingue solitamente una livellazione a lungo raggio da quella a breve raggio: in quest’ultima non si prendono in considerazione le correzioni per la sfericità della terra e per gli effetti della rifrazione atmosferica, come nel caso della maggior parte dei rilievi a scopi ingegneristici. La portata massima della livellazione da un estremo non supera i 10 km. Schemi di rilievo isodeterminati trovano scarsa utilizzazione nelle applicazioni topografiche. Al contrario, gli schemi iperdeterminati, che prevedono misure in soprannumero, consentono la compensazione, cioè la geometrizzazione della figura che i dati di misura, affetti da errori, non riescono a definire; offrono, inoltre, la possibilità di valutare l’attendibilità e l’accettabilità dei risultati, secondo criteri statistico-probabilistici, ed entro certi limiti portano a un incremento della precisione. Esempi di iperdeterminazioni si hanno in poligonali rilevate con appoggi intermedi e/o a entrambi gli estremi; in reti con collegamenti tra vertici non solo in numero sovrabbondante ma anche con misure di tipo diverso ecc.
Procedimenti di misure satellitari
I procedimenti di misure satellitari spesso integrano quelle terrestri come, per es., il sistema di posizionamento GPS (➔). I concetti di base introdotti, per es. quelli relativi a poligonali o reti, restano validi ma i vertici vanno ora riguardati come insiemi di punti non direttamente collegati, bensì inseriti nel sistema satellitare. Dal punto di vista operativo si è quindi svincolati da condizioni di intervisibilità e i problemi nuovi di carattere strettamente topografico si riconducono alle trasformazioni da operare per passare da un sistema a un altro, per es. dal sistema satellitare a quello locale. Per conseguire precisioni prossime a quelle del rilevamento terrestre, i dati GPS provengono da misure differenziali, cioè riferite a un’altra stazione con acquisizione simultanea dei dati. Tra i diversi metodi di rilevamento GPS, quello statico-rapido risulta molto rispondente alle esigenze del rilievo di zone comprese entro 15 km, sostituendo bene le operazioni terrestri di poligonazione e triangolazione locale e operando bene nel campo del rilievo di dettaglio, nelle operazioni di agrimensura ecc.; la stazione di riferimento è in un punto centrale della zona e uno o più ricevitori mobili si trovano in punti di dettaglio. Gli apparati GPS che utilizzano l’apposita rete di satelliti sono costituiti essenzialmente da un’antenna per la ricezione delle onde trasmesse dai satelliti, da un hardware comprendente un orologio di precisione, un sintonizzatore, un gruppo di decodifica, un microprocessore di elaborazione, e da un software per la gestione dei processi di acquisizione e memorizzazione.
Medicina
La proiezione, sul corrispondente piano superficiale, di un organo profondo, per es., la proiezione del cuore e dei grossi vasi sulla regione precordiale. In particolare, t. cranio-cerebrale, ramo dell’anatomia chirurgica che studia i rapporti esistenti tra la scatola cranica e le sottostanti strutture encefaliche. L’anatomia topografica è il ramo dell’anatomia che studia gli organi sinteticamente, in base alla sede che occupano e ai reciproci rapporti.