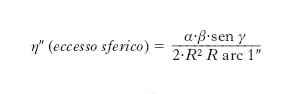triangolazione

triangolazione In geodesia e topografia, metodo di rilievo per la determinazione delle coordinate planimetriche di punti del terreno.

Metodo generale

Nel 1617 il geodeta olandese W. Snellius ideò il metodo della t. per misurare la lunghezza di un arco di meridiano e le coordinate dei punti posizionati sulla superficie terrestre; il procedimento, applicato ovunque, è stato generalizzato in campo geodetico e topografico fino ai giorni nostri.

La t. si basa sul concetto geometrico che 3 punti del terreno, A, B, C, possono essere considerati i vertici di un triangolo di posizione da determinare. In tutta l’estensione territoriale la molteplicità di triangoli contigui, aventi in comune lati e punti di vertice, dà luogo alla rete di triangolazione. In ogni triangolo, da ciascun vertice, viene misurato l’angolo compreso tra le direzioni agli altri 2, utilizzando strumenti ottico-geometrici di precisione, detti teodoliti. I 3 angoli planimetrici α, β, γ (detti angoli azimutali) nei 3 vertici A, B, C devono soddisfare la condizione geometrica di chiusura angolare del triangolo, ossia la sommatoria dei tre angoli interni deve essere pari a un angolo piatto π. Per ridurre l’entità dei lievi (in genere pochi secondi d’arco) ma inevitabili errori di misurazione degli angoli, ciascun angolo α, β, γ viene misurato più volte applicando il metodo operativo della reiterazione; la media delle letture così ottenute è, naturalmente, il valore più probabile dell’angolo al vertice considerato. La differenza tra la sommatoria dei tre angoli α, β, γ e il valore della condizione π costituisce l’errore di chiusura angolare ±ε del triangolo, ossia: α+β+γ=π±ε. Per assicurare il rigore geometrico della figura triangolare, l’errore ε è ripartito fra i 3 angoli vertice (operazione di compensazione), attribuendo a ciascuno di essi il valore 1/3ε con il segno della correzione, naturalmente opposto a quello dell’errore di chiusura. Per rendere altresì geometrica tutta la rete di t., si procede anche a un complesso calcolo di compensazione con il quale, oltre che agli angoli, vengono attribuiti anche i più opportuni valori alle lunghezze dei lati della maglia affetti da errori, seppur lievi, di determinazione. Diversamente i triangoli non chiuderebbero. Infatti le lunghezze dei lati dei triangoli vengono calcolate partendo da una iniziale base geodetica misurata, di sviluppo contenuto, in genere, entro 5-10 km, utilizzando barre o fili di acciaio invar di lunghezza determinata con elevatissima precisione in apposito laboratorio. In tal modo si può assicurare di non commettere errori superiori a ±1 mm per kilometro di lunghezza della base (precisione di ordine geodetico). Con operazioni di sviluppo, utilizzando una piccola rete di t. locale, si determina il primo lato della maglia e poi tutti i rimanenti lati, risolvendo ogni triangolo in sequenza nell’ambito di un blocco della rete. Le maglie triangolari delle reti fondamentali che ricoprono interi Stati hanno lati di lunghezza media intorno ai 30-50 km (talvolta nei collegamenti con le isole si va ben oltre); i limiti risiedono, soprattutto, nella intervisibilità e nella osservabilità strumentale reciproca tra i vertici con cui avviene il collegamento, tenuto anche conto degli effetti negativi della curvatura terrestre.

Reti di triangolazione

La configurazione geometrica ottimale della rete è quella che ha triangoli di forma equilatera; pertanto, per quanto possibile, all’impianto della rete si scelgono sul terreno punti di vertici (detti trigonometrici) topograficamente caratteristici, distribuiti in modo pressoché uniforme, compatibilmente con le caratteristiche morfologiche del terreno, assicurando il collegamento di ogni vertice con gli altri punti trigonometrici a giro d’orizzonte. Per questo motivo si scelgono quali vertici trigonometrici punti dominanti, come vette di montagne, cime di colline, oppure sommità di campanili o di edifici. Questi vertici vengono materializzati con centrini a terra cementati, oppure scegliendo particolari caratteristici dei manufatti ben collimabili da lontano, come croci di campanili, merli di torri, comignoli sui tetti ecc., che vengono descritti in apposite monografie per la consultazione e l’individuazione in campagna.

I triangoli con lati di lunghezza di 30-50 km sono quelli che nella geodesia classica vengono denominati triangoli di I ordine (e i vertici sono i punti trigonometrici di I ordine) e costituiscono la rete fondamentale; poiché sono di dimensioni molto grandi, per necessità di pratica utilizzazione geodetico-topografica le reti di I ordine vengono infittite con triangoli interni collegati ai precedenti e con lati che, pertanto, sono via via più corti (reti di II, III, IV ordine) sino a ottenere lati di triangoli di 4-5 km di lunghezza. La moderna tecnologia consente altresì di misurare direttamente le lunghezze dei lati dei triangoli con strumentazioni elettrottiche denominate geodimetri, che utilizzano fasci di luce a sorgente laser o a infrarossi, o di lampade a vapori di mercurio, che vengono emessi e modulati dall’emittente secondo frequenze prestabilite; la stazione master è posta su un vertice, mentre superfici riflettenti (prismi o specchi appositi) costituiscono la stazione secondaria ubicata sull’altro vertice estremo del lato. Infatti la misura avviene mediante il confronto strumentale dello sfasamento che si manifesta nelle unità elettrottiche durante il percorso del fascio di luce nel tragitto di andata e di ritorno tra la stazione master e la stazione riflettente. Introducendo nel calcolo i dati meteorologici del momento (temperatura dell’aria e pressione atmosferica), si ottengono unità elettrottiche di misura, di elevata precisione, che possono assicurare determinazioni della distanza con incertezze di ±D∙10–6 (ossia incertezze di ±1 mm per kilometro della distanza D misurata). Si può quindi parlare di operazioni di trilaterazione se si fanno misure dirette in ogni lato del triangolo mediante i distanziometri di cui sopra.

In realtà la superficie su cui si compiono queste operazioni è la superficie geoidica, ossia quella del livello medio del mare che è una superficie equipotenziale; essa si presenta con profilo a curvatura irregolare perché, essendo il geoide di origine gravimetrica, questa superficie varia localmente da zona a zona a causa della diversità di densità e di distribuzione delle masse della crosta terrestre. Per avvalersi di una superficie di base a curvatura regolare simile a quella terrestre, esprimibile mediante relazioni matematiche, i geodeti hanno adottato l’ellissoide, solido generato dalla rotazione di un’ellisse biassiale attorno al proprio asse minore posto in coincidenza con l’asse di rotazione terrestre e con valori parametrici tali da rendere minimi gli scostamenti tra la superficie ellissoidica e quella geoidica. Determinate mediante stazioni astronomiche le coordinate geoidiche di un certo numero di punti materiali prescelti, esse vengono considerate come coordinate geografiche sull’ellissoide terrestre, stabilendo così le corrispondenze di posizione e metriche tra le due superfici suddette. È da dire altresì che l’ellissoide deve essere orientato e che le superfici vengono tra loro ‘bloccate’ per evitare scorrimenti relativi fissando un punto di contatto tra esse (detto punto di emanazione); in questo punto si esegue la stazione astronomica fondamentale e si misura l’azimut a un punto trigonometrico lontano, opportunamente ubicato, per orientare l’ellissoide relativamente a una vasta area geografica.

v. fig.

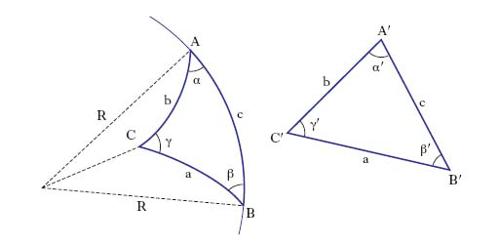
Per quanto attiene alla superficie di riferimento su cui si eseguono le t., considerata ellissoidica, si dimostra che per zone la cui ampiezza non ecceda i 150 km di raggio attorno a un punto centrale (superficie di campo di Weingarten), si può molto vantaggiosamente sostituire all’ellissoide la sfera locale (raggio medio R=6.370 km), la cui geometria è molto più semplice. In altri termini, nei limiti sopra posti, i valori di posizione dei punti sull’ellissoide non si discostano da quelli determinati come se fossero posti sulla sfera. È da tenere presente, quindi, che gli angoli al vertice α, β, γ nei triangoli terrestri sono in realtà angoli sferici i quali (v. fig.) differiscono dagli angoli piani α′, β′, γ′ di una quantità detta eccesso sferico (➔ trigonometria), che, per il teorema di Cavalieri, vale il rapporto:

T. aerea

In fotogrammetria viene largamente impiegata la t. aerea, che permette di ricavare dai fotogrammi le coordinate di un gran numero di punti. Ne esistono due tipi: la t. aerea radiale, che permette di ricavare le sole coordinate planimetriche, e la t. aerea spaziale, che consente di ottenere planimetria e altimetria. Le t. radiali (generalmente a punto nadirale) si attuano su terreni piani; congiungendo i punti principali delle successive fotografie si viene a tracciare nello spazio una poligonale aerea alla quale corrisponde un’identica poligonale sul terreno. Gli angoli di tale poligonale possono essere agevolmente misurati sui fotogrammi, mentre i lati possono essere calcolati successivamente, a condizione che sui primi due fotogrammi figurino le immagini di due punti noti del terreno. Le t. spaziali servono per il rilievo di terreni piani e non piani; per esse si adopera il metodo delle coppie di fotogrammi concatenate, così detto perché una volta realizzato nel restitutore l’orientamento della prima coppia (a mezzo della posizione nota di almeno due punti del terreno), l’orientamento delle successive coppie si realizza con riferimento a punti restituiti dei fotogrammi precedenti cadenti nelle zone di ricoprimento, annullando le relative parallassi di altezza.

T. satellitare

Con l’avvento della tecnologia satellitare anche la geodesia operativa ha fatto progressi. Vi furono varie ricerche e sperimentazioni negli anni 1970 con satelliti-pallone (per es., venne utilizzato il satellite PAGEOS, pallone di 30 m di diametro che orbitò per molti anni attorno alla Terra) per determinare la posizione di vertici trigonometrici. A quei primi sistemi, che pure avevano dato notevoli risultati, ne sono subentrati altri più sofisticati. Attualmente è operativo il sistema GPS (➔), i cui satelliti svolgono la funzione di vertici trigonometrici mobili nello spazio, realizzando un’intersezione spaziale a vertice di piramide, in cui l’antenna a terra è il vertice e la posizione dei satelliti nello spazio è la base.

Esiste una tecnica più precisa della precedente, nota come metodo del posizionamento differenziale; essa si basa sulla differenza di posizione del punto da determinare rispetto a un altro che invece è di coordinate note (vertice trigonometrico). Si ottiene una baseline, cioè un vettore che rappresenta la distanza tra i due punti. Ciò impone di poter disporre di due ricevitori collocati agli estremi della baseline. La tecnica differenziale si basa sulla misura di ‘fase’ con cui si riesce a ridurre le incertezze del valore della lunghezza d’onda del segnale per effetti di atmosfera e troposfera. La misura di fase consiste nel confronto tra la fase della portante che proviene dal satellite, che, per effetto Doppler, si sfasa durante il tragitto verso il punto di stazione, e la fase di replica, di uguale frequenza, originata nel ricevitore.