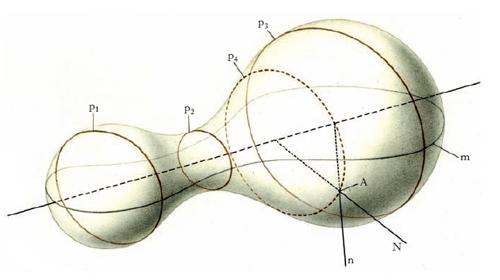
geodetica
Linea tracciata sopra una superficie e tale che in ogni suo punto la normale principale a essa coincida con la normale alla superficie in quel punto; ovvero tale che il piano osculatore alla linea risulti normale alla superficie in quel punto; per es., le g. della superficie sferica sono le circonferenze massime. Più in generale, sopra una superficie di rotazione (v. fig.) sono g. tutti i meridiani m, ma tra i paralleli sono g. solo quelli di raggi minimo e massimo; così, i paralleli p1, p2, p3 sono g. mentre p4 non lo è: infatti, nel punto A, la normale principale N a p4 è diversa dalla normale n alla superficie. Un’importante proprietà delle g. è che esse risultano linee di minima lunghezza: su una prefissata superficie, cioè, la linea di lunghezza minima tra due punti della superficie stessa è un arco di geodetica. Segue da ciò che le g. del piano sono le rette. Il concetto di g. sopra una superficie ordinaria si estende a quella di g. sopra superfici o varietà dotate di una metrica la quale permetta di dare senso alla ‘lunghezza’ di una linea. Lo studio della g. di una superficie e, più in generale, di una varietà differenziabile è uno dei capitoli della geometria differenziale più studiati e più ricchi di problemi.