cruciforme, curva

fig

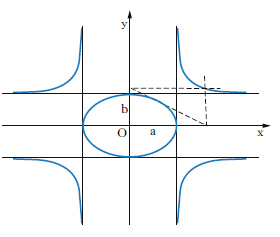
Curva del 4° ordine. Data un’ellisse, la curva c. è il luogo dei punti d’incontro delle rette parallele agli assi dell’ellisse condotte per i punti in cui questi ultimi sono intersecati da una retta variabile tangente all’ellisse stessa (v. .). Assunti gli assi cartesiani coincidenti con gli assi dell’ellisse, che allora viene rappresentata dall’equazione x²/a²+y²/b²=1, la curva c. ha equazione x²y²=b²x²+a²y²; è una quartica con 3 biflecnodi: uno (isolato) nell’origine e due (a tangenti reali: gli asintoti x=±a, y=± b) nei punti impropri degli assi coordinati. Rientra fra le curve di Lamé.