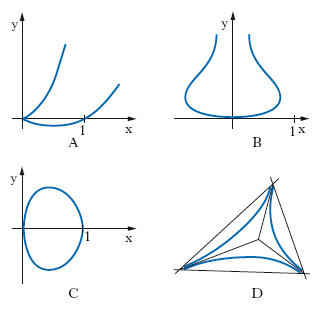quartica
In geometria, varietà algebrica del quarto ordine; in particolare, q. razionale normale è la curva dello spazio a 4 dimensioni di equazioni x1=t, x2=t2, x3=t3, x4=t4.
Le q. si distinguono in q. piane e q. sghembe (o gobbe). La q. piana è una curva piana rappresentata da un’equazione di quarto grado in x, y; un esempio è la lemniscata di Bernoulli. Il classico teorema di Steiner per le coniche si generalizza alle q. (e anzi alle curve algebriche piane di ordine qualsiasi) nel seguente modo: scelti 4 punti qualunque P1, P2, P3, P4 su una q., le rette che da ciascuno di essi proiettano un punto P mobile sulla q. danno luogo a una tetralinearità tra i fasci di rette con centri nei punti P1, …, P4; viceversa, ogni q. piana si può ottenere a partire da una tetralinearità tra 4 fasci di rette. Una q. irriducibile può avere fino a 3 punti doppi, e in questo caso è razionale; se al contrario i punti doppi sono 2, 1 o nessuno, la q. ha rispettivamente genere 1, 2 o infine 3 e non è più razionale. La q. in fig. 1A ha un punto doppio cuspidale nell’origine e un tacnodo all’infinito: è perciò razionale e rappresentabile nella forma x=1/t2, y=(1−t)/t4. La q. in fig. 1B ha un unico punto doppio all’infinito e perciò il genere è 2. La q. in fig. 1C è un ovale con due punti doppi (due cuspidi nei punti ciclici), la q. ha perciò genere 1, ossia è ellittica (essa si può rappresentare parametricamente mediante funzioni ellittiche). Infine, la fig. 1D indica una q. razionale tricuspidata: si dimostra che tutte le q. di tale tipo sono trasformabili l’una nell’altra mediante un’opportuna omografia e che, in ogni caso, le tre tangenti cuspidali passano per uno stesso punto.
La q. sghemba (o gobba) di prima specie è la linea C, intersezione di 2 quadriche Q, Q′ e perciò è anche la curva base del fascio di quadriche individuato appunto da Q, Q′. Indicati con V1, …, V4 i vertici dei 4 coni appartenenti al fascio e con t una retta tangente a C, si dimostra che il birapporto dei 4 piani che da t proiettano i punti V1, …, V4 non dipende da t: esso è un invariante proiettivo della curva. Una q. di prima specie non ammette, in generale, punti doppi e perciò ha genere 1 ed è rappresentabile parametricamente mediante funzioni ellittiche; se al contrario possiede un punto doppio (ciò accade se le quadriche Q, Q′ sono tangenti in un punto) diviene una curva razionale.
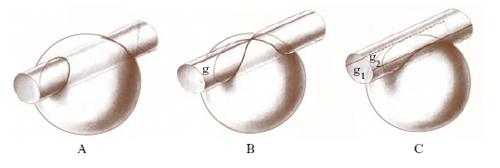
Dal punto di vista dell’andamento, le q. di prima specie senza punto doppio si distinguono in monogrammiche e digrammiche a seconda che la curva sia costituita da un solo circuito o da due; per es., l’intersezione di una sfera con un cilindro rotondo avente diametro inferiore a quello della sfera è una q. digrammica se tutte le generatrici del cilindro sono secanti la sfera (fig. 2A) ed è monogrammica se due generatrici sono tangenti alla sfera (g1, g2 in fig. 2C). Se, infine, tutte le generatrici sono secanti salvo una che è tangente (g in fig. 2B) si ha una q. con punto doppio: ciò avviene, in particolare, nel caso della finestra di Viviani (➔ Viviani, Vincenzo).
La q. sghemba (o gobba) di seconda specie è la linea L intersezione incompleta di una superficie cubica e di una quadrica le quali abbiano in comune due rette r, r′ tra loro sghembe (intersezione incompleta significa che si debbono trascurare le rette r, r′). Una q. di seconda specie è sempre razionale e può ammettere eventualmente un punto doppio; in tal caso essa è contemporaneamente una q. di prima specie. Ogni q. di seconda specie si può ottenere partendo da una schiera rigata S e da tre piani α, β, γ, e scegliendo, su ogni retta di S, il punto P tale che il birapporto che P forma con i punti nei quali r attraversa α, β, γ, abbia un valore assegnato. In particolare è una q. di seconda specie il luogo dei punti medi dei segmenti intercettati da due piani π, π′ sulle rette di una delle due schiere di una quadrica.