decremento

Enciclopedia on line

fig.

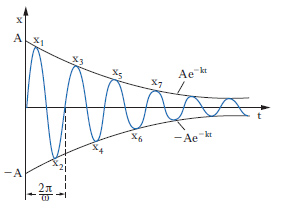
In fisica, essendo data una grandezza oscillante smorzata, cioè rappresentabile con una funzione del tipo x(t)=Ae–kt sen (ωt+ϕ), dove A, k, ω, ϕ, sono delle opportune costanti, e è la base dei logaritmi naturali, t una variabile (generalmente il tempo), si chiama d., o d. numerico, il rapporto, costante, tra due massimi successivi del medesimo segno. Tale rapporto risulta pari a ekT, essendo T=2π/ω il periodo della grandezza; si ha: ekT=x1/x3=x2/x4=...=xn/xn+2 (v. fig.).

La grandezza k ha il nome di fattore di smorzamento; la quantità δ=kT=ln(x1/x3)= ln(x2/x4)=... viene detta d. logaritmico.

Vedi anche
meno Il segno (−) che rappresenta l’operazione di sottrazione; per es., 5−3 rappresenta la differenza tra i numeri cinque e tre. Lo stesso segno si usa per indicare un numero negativo. Analogamente, l’opposto di un numero relativo n si rappresenta con il simbolo −n. Nelle indicazioni di temperatura, si indicano ... grandezza fisica G. fisica Qualsiasi ente suscettibile di una precisa definizione quantitativa, quindi di misurazione, che viene introdotto allo scopo di consentire una descrizione quantitativamente precisa di fenomeni fisici e la traduzione in equazioni matematiche di problemi della fisica. G. dimensionata è ... applicazione Matematica Il concetto di a. è una generalizzazione del concetto classico di funzione (➔ corrispondenza). Si parla di a. di un insieme P in un insieme Q, quando tra i due si stabilisce una corrispondenza del tipo seguente: a ogni elemento di P corrisponde un ben determinato elemento di Q, mentre un elemento ... rapporto Legame, relazione, connessione tra due o più elementi. Diritto R. giuridico è la relazione tra due (o più) soggetti regolata dal diritto. La nozione di r. giuridico Caratteristica del diritto, è quella di regolare i r., giuridicamente rilevanti perché hanno come oggetto interessi suscettibili di valutazione ...
Categorie
Tag
Vocabolario
decreménto
decremento decreménto s. m. [dal lat. tardo decrementum, der. di decrescĕre «diminuire»]. – Il decrescere, decrescenza, diminuzione. In fisica, data una grandezza oscillante smorzata, si chiama d. numerico (o assol. decremento) il rapporto...
decrèmetro
decremetro decrèmetro (o decrìmetro) s. m. [comp. di decre(mento) e -metro]. – Apparecchio (di solito costituito da un oscillografo a raggi catodici) per la misurazione del decremento logaritmico di oscillazioni elettriche.