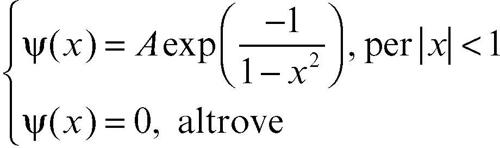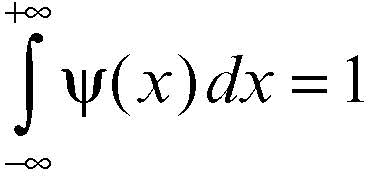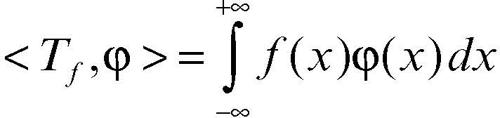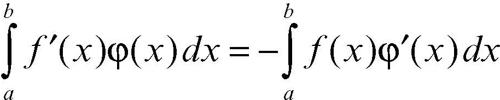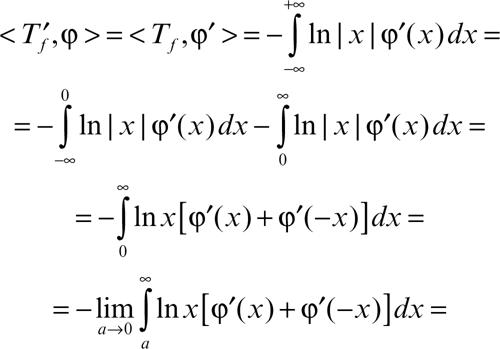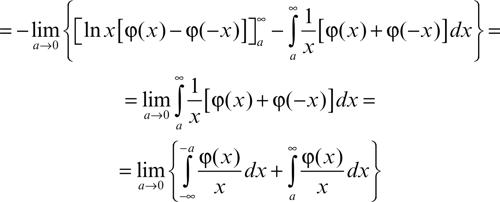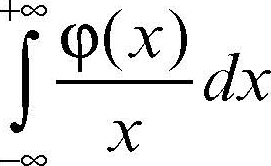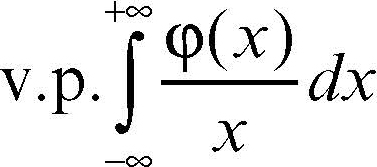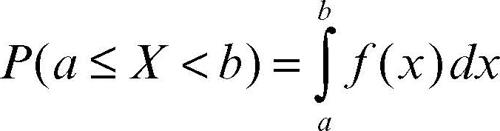distribuzione

distribuzione

distribuzione termine che assume significati diversi a seconda del particolare ambito matematico.

La distribuzione come funzione generalizzata

In analisi, si indica come distribuzione una generalizzazione del concetto di funzione, adatta a descrivere con un unico formalismo sia grandezze diffuse sia grandezze concentrate (si pensi, per esempio, a una massa o a una carica elettrica). Per tale descrizione è indispensabile abbandonare la definizione “puntuale” di funzione, per introdurne una legata a una struttura funzionale: le distribuzioni vengono così definite come elementi del duale di uno spazio opportuno.

Le definizioni principali sono qui date in una sola variabile. Sia Ω un aperto di R e si consideri lo spazio D(Ω) delle funzioni fondamentali (dette anche funzioni test) cioè delle funzioni φ dotate delle due seguenti proprietà:

• φ ∈ C^∞(Ω), è cioè dotata di derivata continua di ogni ordine;

• φ(x) ≡ 0 fuori da un compatto K ⊆ Ω (φ è cioè nulla all’esterno dell’insieme K = supp(φ) detto supporto).

Per esempio, in R una funzione del genere è data da ψ(x), così definita:

che ha supp(ψ) = [0, 1], con il coefficiente A scelto in modo che

Senza definire esplicitamente la topologia dello spazio D(Ω), si può introdurre la nozione di limite di una successione {φ_n} come segue:

• esiste un compatto K tale che tutte le φ_n si annullino fuori da K;

• la successione {φ_n} converga uniformemente a φ assieme alle sue derivate di ogni ordine.

Una distribuzione T è allora un funzionale lineare su D(Ω), il cui valore si designa con <T, φ>, continuo nel senso che <T, φ_n> → <T, φ> ogniqualvolta φ_n → φ nel senso sopra precisato. La notazione <..., ...> è detta crochet ed è utilizzata appunto per la valutazione di una distribuzione. L’insieme delle distribuzioni è, quindi, lo spazio D′ (Ω), duale di D(Ω).

A ogni funzione

cioè integrabile nel senso di Lebesgue (→ Lebesgue, integrale di) su ogni compatto contenuto in Ω, e in particolare a ogni funzione continua, corrisponde una distribuzione T_ƒ ∈ D′ (Q) definita da

(si osservi che l’insieme di integrazione in realtà coincide con supp(φ)). Per tutti i valori t in cui ƒ è continua si ha

dove ψ_n,t (x) = nψ(n(t − x)) e ψ è la funzione sopra introdotta. Per questo motivo T_ƒ è talvolta chiamata coordinata generalizzata di ƒ. Per le usuali funzioni, la conoscenza dei valori ƒ(x), “nei punti x di R” equivale perciò a quella “nei punti φ di D”, cioè delle dualità <T_ƒ, φ>. Una distribuzione di questo tipo, cioè rappresentabile in tale forma, si dice distribuzione regolare. Esistono tuttavia altri funzionali lineari e continui su D(Ω), corrispondenti a distribuzioni singolari, che non provengono da funzioni. L’esempio più semplice e famoso di distribuzione singolare è dato dalla cosiddetta delta di Dirac, definita da: <δ, φ>> = φ(0) (→ Dirac, delta di). Si dimostra che non può esistere alcuna funzione

per cui T_ƒ = δ.

Non ha senso in generale dire quale valore assume una distribuzione in un punto, ma si dice che una distribuzione è nulla in un aperto W se <T, φ> = 0 per ogni φ, con supp(φ) ⊆ W. Il supporto di una distribuzione T è allora l’insieme supp(T) tale che nell’aperto complementare T è nulla. Per esempio, per la distribuzione δ di Dirac, si ha supp(δ) = {0}, in quanto se supp(φ) non contiene l’origine è <δ, φ> = φ(0) = 0. Quindi δ è nulla fuori dall’origine, pur non assumendo alcun valore nell’origine.

Le distribuzioni godono di importanti proprietà qui di seguito elencate.

a) Ogni distribuzione è derivabile, secondo la definizione di derivata distribuzionale <T′, φ > = + − <T, φ′>, e quindi è derivabile infinite volte. Tale formula, per distribuzioni regolari che provengono, nel senso precisato sopra, da funzioni di classe C¹, è mutuata dalla formula di integrazione per parti: infatti, se supp(φ) ⊆ [a, b],

in quanto φ(a) = φ(b) = 0. La regola appare quindi dettata dal principio di permanenza delle proprietà formali che regola in genere le estensioni di un concetto matematico. Per esempio, la derivata della funzione di Heaviside Y(x) è la δ di Dirac; a sua volta la derivata di δ è la distribuzione δ′ definita da <δ′, φ> = −φ′(0) e in generale <δ>⁽ⁿ⁾, φ> = (−1)ⁿφ⁽ⁿ⁾(0). In un modello fisico in cui ƒ rappresenti per esempio un carico distribuito su un’asta, δ rappresenta un carico concentrato e δ′ un momento concentrato; in un modello elettrico, δ rappresenta una carica puntuale e δ′ un dipolo elettrico concentrato.

Un esempio utile per comprendere la differenza tra derivata classica e derivata nel senso delle distribuzioni è dato dalla funzione

In senso classico, essa è derivabile fuori dall’origine e la sua derivata è ƒ′ (x) = 1/x. Tale funzione non appartiene a

perché 1/x non è integrabile in un intorno dell’origine, e dunque non è una distribuzione. Nel senso delle distribuzioni, la derivata di T_ƒ si calcola come segue:

Questo limite è detto valore principale secondo Cauchy dell’integrale:

(che non converge nel senso usuale) e si denota come

Pertanto è

Si badi però che anche per una funzione continua la derivata nel senso delle distribuzioni non coincide necessariamente con la derivata usuale, neppure se essa esiste quasi ovunque, come per la funzione di → Vitali, o addirittura ovunque, come per la funzione

a meno che ƒ non sia assolutamente continua (→ continuità).

b) Se T_n → T nel senso delle distribuzioni, cioè se <T_n, φ> → <T, φ>, ∀φ test, anche

cioè è sempre lecita la derivazione per successioni.

c) Ogni distribuzione T ammette una primitiva S, definita a meno di una costante. Per esempio, come già detto, una primitiva di δ è la funzione di Heaviside.

d) Non si può definire il prodotto di due distribuzioni, ma solo quello di una distribuzione T per una funzione γ ∈ C^∞(Ω): infatti, già il prodotto di due funzioni di

non appartiene in genere a tale spazio. Il prodotto Tγ si definisce ponendo <Tγ, φ> = <T, γφ>. Per esempio:

Quindi: δ′(3x + 5) = 5δ′ − 3δ. Il prodotto può essere nullo anche se T e γ non sono nulle; per esempio, δx = 0, in quanto ∀φ test risulta

e) Per il prodotto sopra definito vale la regola di derivazione di Leibniz (Tγ)′ = T′γ + Tγ′.

f) La traslata di una distribuzione è definita dalla formula <T_(h), φ> = <T, φ_(−h)>, dove φ_(−h)(x) = φ(x + h). Per esempio, <δ>_(h), φ> = <δ, φ>_(−h)> = φ(0 + h) = φ(h). Si mostra che la derivata T′ è il limite per h → 0 del rapporto incrementale (T_(−h) − T)/h, limite che esiste senza eccezioni.

g) Ogni distribuzione a supporto compatto è di ordine finito, è cioè la derivata di un ordine opportuno di una funzione continua. Tali sono δ e le sue derivate. Invece la distribuzione T definita da

è di ordine infinito.

h) Il prodotto di convoluzione (detto anche, semplicemente, convoluzione) di due distribuzioni T e S è definito solo in casi particolari, tra cui è importante quello in cui almeno una delle due sia a supporto compatto (un altro caso, utile nelle applicazioni alla trasformata di Laplace, è quello in cui tutte le distribuzioni abbiano supporto limitato a sinistra). Si pone allora

avendo indicato con T(x) la distribuzione T che agisce sulla variabile x e così per S(y). La distribuzione delta si comporta come unità rispetto alla convoluzione δ ∗ T = T; le sue derivate e le sue traslate generano per convoluzione le derivate e le traslate di T: δ′ ∗ T = T′, δ_(h) ∗ T = T_(h).

La derivata e la traslata di un prodotto di convoluzione si ottengono derivando o traslando uno qualsiasi dei fattori:

La convoluzione è commutativa e associativa se tutte le distribuzioni, tranne al più una, sono a supporto compatto. Altrimenti la proprietà può essere falsa:

mentre

Qui la funzione Y (funzione di Heaviside) e la costante 1 non hanno supporto compatto.

Queste proprietà si generalizzano in Rⁿ: la definizione di derivata parziale <∂T/∂x_k, φ> = − x_k> corrisponde, nel caso di distribuzioni regolari, all’uso delle formule di Gauss-Green (→ Green, formule di). La formula si generalizza a derivate di ordine superiore. Per esempio, la delta di Dirac in due variabili, δ_(0,0), definita da <δ>_(0,0), φ> = φ(0, 0), è la derivata seconda mista della funzione caratteristica del primo quadrante, che si può esprimere come prodotto di due funzioni di Heaviside: U = Y(x)Y(y). È cioè ∂²U/∂x∂y = δ_(0,0). Ne segue che la funzione U è la soluzione fondamentale dell’equazione iperbolica ∂²U/∂x∂y = ƒ.

Le distribuzioni temperate sono invece gli elementi dello spazio S′ (Rⁿ), duale dello spazio S(Rⁿ) delle funzioni a decrescenza rapida, cioè delle funzioni che insieme alle loro derivate di ogni ordine si annullano all’infinito più rapidamente di qualsiasi potenza del tipo 1/xⁿ, con n > 0. Più precisamente sono le funzioni φ ∈ C^∞(Rⁿ) che tendono a 0 per ‖x‖ → ∞ più rapidamente di ogni potenza ‖x‖⁻ⁿ assieme a tutte le loro derivate di ogni ordine. Per esempio, la funzione φ = exp(−‖x‖²) è a decrescenza rapida.

Lo spazio S′ (Rⁿ) delle distribuzioni temperate è un sottospazio proprio di D′ (Rⁿ) e in esso, oltre alle proprietà precedenti, è possibile generalizzare alle distribuzioni la trasformata di Fourier, mediante la formula

Il nome di distribuzione temperata nasce dal fatto che non tutte le funzioni ƒ(x) continue (o localmente integrabili) su Rⁿ appartengono allo spazio S′ (Rⁿ), ma solo quelle a crescita lenta all’infinito, cioè per cui ƒ(x) ≤ A ‖x‖ⁿ per x → ∞. Per un inquadramento teorico della distribuzione come funzione generalizzata si veda la voce → distribuzioni, teoria delle.

La distribuzione in statistica e probabilità

È l’insieme delle modalità e delle relative intensità con cui si è manifestato o ci si aspetta che si possa manifestare un fenomeno. A seconda che ci si riferisca al passato (o all’esame dei dati di un campione) oppure a una valutazione sul futuro (o a una ipotetica generalizzazione dei dati di un campione all’intera popolazione), occorre teoricamente distinguere tra due tipi di distribuzione, la distribuzione statistica e la distribuzione di probabilità, anche se, dal punto di vista della terminologia, della formalizzazione matematica e della rappresentazione, i due tipi hanno molti aspetti in comune. Se la distribuzione riguarda un solo carattere (o una sola variabile aleatoria), essa è detta distribuzione semplice o univariata; se ne riguarda due è detta distribuzione doppia; se ne riguarda più di due, è detta distribuzione multipla o multivariata. Una distribuzione è discreta se tale è il carattere o la variabile cui si riferisce, se cioè l’insieme dei suoi possibili valori è finito o numerabile, altrimenti è una → distribuzione continua.

Qualunque sia il tipo, di una distribuzione si evidenziano sempre alcuni indici sintetici, che possono essere di tipo centrale o di posizione (→ media, → moda, → mediana) oppure relativi alla dispersione o variabilità dei dati rispetto ai valori centrali (→ scarto quadratico medio, → varianza, → differenze medie).

☐ In una distribuzione statistica (o di dati statistici) le modalità si riferiscono a uno o più caratteri statistici e le relative intensità sono le frequenze, che derivano, generalmente, da una raccolta dei dati attraverso questionari, esperimenti, osservazioni di un fenomeno ecc. Le frequenze possono essere assolute o relative: una distribuzione di frequenze assolute si trasforma in distribuzione di frequenze relative considerando i rapporti

in cui n_i rappresenta la frequenza assoluta di una singola generica modalità, f_i la sua frequenza relativa, n il numero totale dei casi osservati e k il numero delle diverse modalità (si veda anche → distribuzione cumulata).

☐ In una distribuzione di probabilità, se la variabile aleatoria è discreta, la funzione di distribuzione di probabilità, per brevità detta anche funzione di probabilità, è la successione dei valori di probabilità P(X = x₁), ..., P(X = x_n) che la variabile aleatoria X assuma le rispettive modalità x₁, ..., x_n. A seconda del fenomeno e del problema in esame si distinguono diverse classi di distribuzioni discrete di probabilità, contraddistinte da leggi e parametri diversi, tra cui: → distribuzione binomiale, → distribuzione geometrica, distribuzione ipergeometrica, distribuzione di → Poisson.

Se invece X è una variabile aleatoria continua, la funzione di probabilità è detta funzione di → densità perché non esprime direttamente la probabilità quanto il suo variare (e, dunque, il suo addensarsi). Per una variabile continua, infatti, la probabilità che essa assuma un valore puntuale è nulla (in termini di definizione classica di probabilità sarebbe un caso favorevole su infiniti possibili) e occorre ragionare per intervalli. La probabilità che X assuma valori compresi tra a e b (con a < b) è allora data dall’area sottesa al grafico della funzione di densità ƒ nell’intervallo dello spazio campionario [a, b), cioè:

Anche nel caso continuo si può costruire l’equivalente continuo della funzione di distribuzione cumulata, cioè la funzione di → ripartizione F, che esprime la probabilità che la variabile X assuma valori minori o uguali a un valore assegnato.

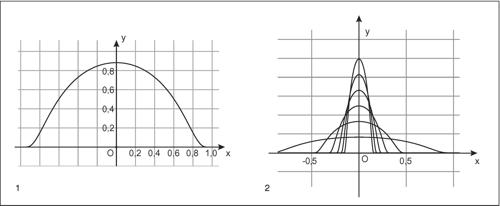
A seconda del fenomeno e del problema in esame si distinguono diversi tipi di distribuzioni continue, contraddistinte da leggi e parametri diversi, tra cui: → distribuzione normale, distribuzione → chi-quadrato, distribuzione F di → Fisher, distribuzione t di → Student.