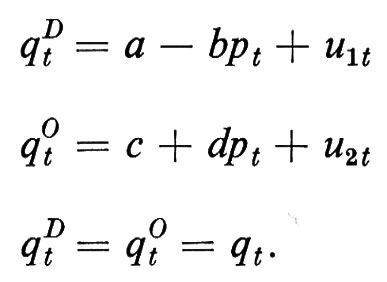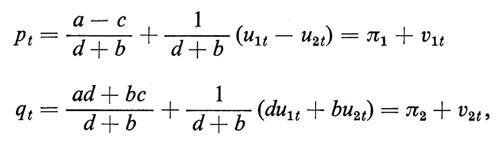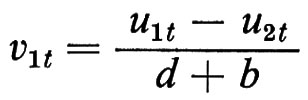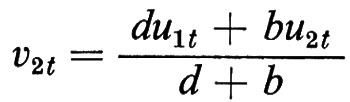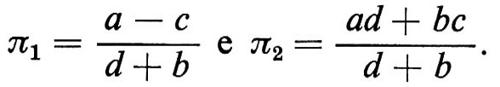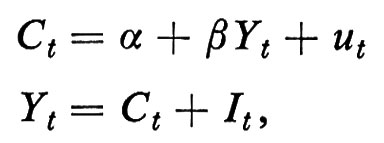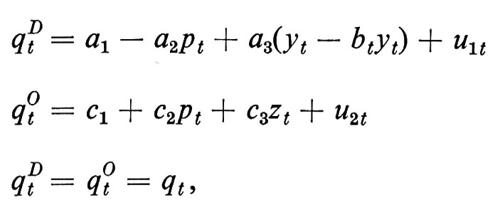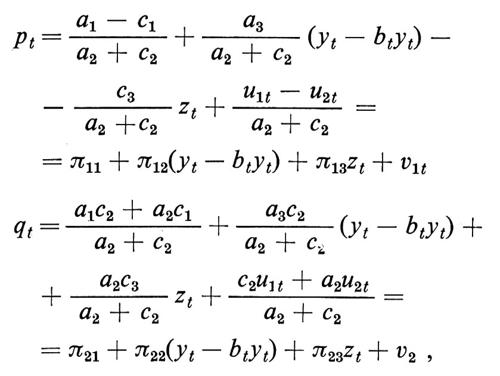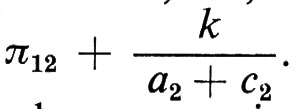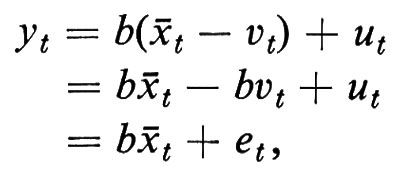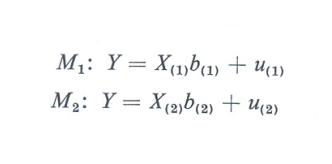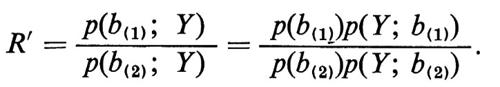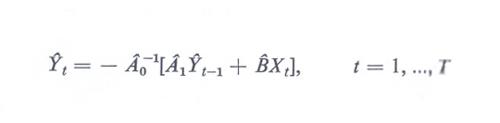Econometria

Econometria

di Luigi Pasinetti, Guido Gambetta

Econometria

sommario: 1. Definizione. 2. I precedenti storici. 3. La nascita dell'econometria. 4. I maggiori centri econometrici. 5. L'econometria come disciplina fra economia e statistica. 6. Dibattiti e problemi irrisolti. 7. Problemi rilevanti. a) Errori di specificazione. b) Scelta fra modelli alternativi. c) Uso dei modelli per la previsione e la valutazione di politiche economiche. □ Bibliografia.

1. Definizione

L'econometria, come lascia capire l'etimologia stessa della parola, è una disciplina che si occupa della quantificazione e della misurazione dei fenomeni economici. Essa fa parte della più ampia branca scientifica che va sotto il nome di ‛economica' o ‛economia' (nella duplice distinzione tra ‛economia politica', più propriamente rivolta alle impostazioni teoriche, e ‛politica economica', più propriamente rivolta alle applicazioni). Ma nello stesso tempo l'econometria rivendica una sua autonomia, proprio con riferimento alla rappresentazione dei fenomeni economici e delle loro relazioni in termini quantitativi e alla loro effettiva misurazione.

Va riconosciuto che i fenomeni economici, e quei comportamenti dei vari individui che sono rilevanti ai fini economici, sono senza dubbio ricchi di aspetti qualitativi, oltre che di aspetti quantitativi, e ciò ha contribuito per lungo tempo a mantenere l'indagine dei fenomeni economici in uno stato di ambiguità per quanto riguarda il metodo di analisi. La necessità di far riferimento a cifre e a serie di dati statistici, nelle forme più varie, è stata avvertita fin dagli albori dell'analisi economica (v. sotto), ma nello stesso tempo è anche sempre stata diffusa la convinzione, o il timore, che il parlare di comportamenti umani in termini meramente quantitativi fosse fonte di eccessiva rigidità o portasse a schemi troppo meccanicistici. In conseguenza di ciò, l'applicazione sistematica dei metodi quantitativi, o ‛econometrici', si è affermata, e si è faticosamente costruita la sua autonomia, soltanto in epoca relativamente recente.

La parola stessa ‛econometria' è stata usata per la prima volta da R. Frisch nel 1926 e la Società Econometrica Internazionale è stata fondata nel 1930 (v. sotto). In questi termini, l'econometria si può senz'altro considerare come una disciplina che, pur avendo dei precedenti storici di rilievo, ha avuto inizio nel Novecento.

2. I precedenti storici

Tentativi vari di applicazione di metodi statistici e matematici allo studio dei problemi economici sono stati effettuati in varie epoche.

L'esempio più notevole è costituito da sir William Petty, parlamentare inglese, medico, matematico, ingegnere e uomo d'affari, il quale nel 1676 scrisse un libro (pubblicato postumo nel 1690), Political Arithmetick, ossia Aritmetica politica, che può senz'altro considerarsi un lavoro di econometria, anche se giudicato con criteri moderni. Petty apparteneva a quella categoria di teorici per i quali ‛scienza' significa ‛misurazione' dei fenomeni indagati. Questo libro esercitò per decenni una rilevante influenza su coloro che trattarono argomenti economici, compresi i classici inglesi della fine del Settecento-inizio Ottocento, nonostante che A. Smith ostentasse indifferenza verso il suo predecessore.

Nel 1711 un ingegnere mantovano, G. Ceva, pubblicò un suo lavoro dedicato alla moneta e ad altri fenomeni economici, e sostenne che per costruire modelli razionali occorre partire da chiare supposizioni e quindi trarne le logiche conclusioni usando la matematica. Un altro grande economista italiano, P. Verri, pubblicò nel 1760 i suoi Elementi di commercio, grazie ai quali egli divenne uno dei primi economisti a presentare una bilancia dei pagamenti, mostrando grande abilità nel collegare teoria economica e ricerca dei fatti concreti. Va inoltre menzionato un altro scrittore italiano, F. Fuoco, che in un suo saggio economico (Pisa, 1827) discusse a lungo ‟l'uso dell'algebra nell'economia politica".

Il caposcuola degli economisti francesi noti come fisiocrati, F. Quesnay, fondò tutte le sue teorie su un leau économique che per comune riconoscimento è considerato il ‛precursore' dell'analisi quantitativa, nota col nome di input-output, proposta da Leontief (v., 1941). Quesnay basò tutti i suoi ragionamenti economici appunto su relazioni, espresse in termini quantitativi, che rappresentavano la produzione e la circolazione dei beni agricoli e manifattuneri nel regno francese della metà del Settecento. I classici inglesi furono sorprendentemente restii a quantificare le loro relazioni, ma un matematico inglese di Cambridge, W. Whewell, lasciò una notevole rappresentazione matematica della teoria ricardiana, mostrando come le relazioni in base alle quali ragionava Ricardo potessero essere espresse in termini matematici, con vantaggio per la chiarezza delle idee e il rigore delle deduzioni.

È pure divenuta nota un'indagine statistica di E. Engel, che nel 1857 pubblicò un lavoro sulla spesa dei lavoratori nella Sassonia. Engel trovò un'uniformità empirica (che venne poi chiamata ‛legge di Engel'), secondo la quale la proporzione del reddito globale dedicata al consumo dei beni alimentari diminuisce via via che il reddito pro capite aumenta.

L'uso della matematica nell'elaborazione economica venne poi introdotto in modo esplicito ed essenziale dalla scuola marginalista nella seconda metà del secolo scorso. Ne fu il precursore A. Cournot, anche se i suoi lavori non ebbero molta fortuna. Più tardi L. Walras, il cui lavoro principale è del 1874, e quindi il nostro V. Pareto presentarono le loro teorie in termini di sistemi di equazioni simultanee. Sia Walras che Pareto avevano avuto una formazione culturale matematica e furono sempre convinti che la matematica fosse essenziale nell'esprimere le loro teorie. Anche i due maggiori esponenti inglesi della scuola marginalista della fine del secolo scorso, W. S. Jevons e A. Marshall, ebbero una formazione culturale matematica, ma si astennero dall'usare esplicitamente la matematica nella presentazione delle loro teorie, preferendo la logica verbale comune e relegando le dimostrazioni matematiche in appendice ai loro lavori. Si arriva così agli anni immediatamente seguenti la prima guerra mondiale, che portarono alla formazione della Società Econometrica Internazionale.

3. La nascita dell'econometria

Può essere utile richiamare gli avvenimenti che stanno dietro l'atto ufficiale di nascita dell'econometria.

Gli anni che seguirono la prima guerra mondiale furono anni di sconvolgimento nel campo delle relazioni economiche internazionali e di diffusa disoccupazione nei paesi industrializzati. Ciò era in stridente contrasto con le situazioni idilliache corrispondenti agli schemi teorici prevalenti. Con la formulazione completa della teoria marginalistica (schema dell'equilibrio economico generale di Pareto) si era diffusa la convinzione che si fosse ormai giunti alla formulazione della ‛teoria economica' per eccellenza. Tutte le elaborazioni precedenti (per esempio quelle dei classici) venivano considerate delle teorie primitive, ormai assorbite o superate dallo schema dell'equilibrio economico generale. Formalmente questa impostazione sembrava ineccepibile. Eppure, preoccupazioni notevoli cominciarono a farsi strada a causa della scarsa connessione tra teoria e realtà empirica. In un articolo sulla rivista ‟Economic journal", apparso nel 1922, l'economista inglese Clapham iniziava una lunga controversia definendo gli strumenti della teoria economica ‟scatole vuote" (empty boxes): belle, eleganti e attraenti, ma prive di contenuto sostanziale.

Avvenne così che un gruppo di economisti, con preparazione matematica e statistica, si convinse che non bastavano più nè la teoria economica, nè la matematica, nè la statistica, quando ciascuna di queste veniva usata in modo isolato. Occorreva l'unificazione dei tre punti di vista. Ed è appunto a questa unificazione che si attribuì il nome di econometria.

Nell'editoriale che Frisch scrisse, nella sua veste di primo direttore della nuova rivista trimestrale ‟Econometrica", che iniziò le pubblicazioni nel 1933, si legge: ‟L'econometria non coincide affatto con la statistica economica. Nè è identica con ciò che si chiama economia teorica in generale, sebbene una considerevole parte della teoria abbia un netto carattere quantitativo. E nemmeno l'econometria è sinonimo di applicazione delle matematiche all'economia. L'esperienza ha mostrato che ciascuno dei tre punti di vista suddetti, quelli della statistica, della teoria economica e delle matematiche, è condizione necessaria ma non sufficiente per l'esatta comprensione delle relazioni quantitative nella vita economica moderna. È la loro unificazione che rende potenti i tre punti di vista. E questa unificazione costituisce l‛econometria".

Può essere inoltre interessante riportare alcuni stralci dell'articolo primo dello statuto della Società Econometrica Internazionale, che ne definisce i fini: ‟La Società Econometrica è una società internazionale per l'avanzamento della teoria economica nei suoi rapporti con la statistica e la matematica [...]. Il suo scopo essenziale è di promuovere quegli studi che portano a unificare l'approccio teorico-quantitativo e l'approccio empirico-quantitativo dei problemi economici e che sono animati da uno spirito metodico e rigoroso simile a quello che è prevalente nelle scienze naturali. Entra nella sfera di interessi della Società tutta l'attività suscettibile di condurre in modo immediato o a più lungo termine a una tale unificazione degli studi teorici e dell'osservazione dei fatti in materia economica".

Va anche aggiunto, per completezza, che l'unificazione della teoria economica, della matematica e della statistica in un'unica disciplina l'econometria è rimasta in molte indagini pur dette ‛econometriche' un'aspirazione, più che un effettiva realtà. Molti studi pur chiamati ‛econometrici', che compaiono nelle riviste scientifiche di economia contemporanea, si limitano a enunciazioni matematiche di relazioni economiche, senza alcun riferimento empirico, e altri presentano stime statistiche di relazioni ad hoc che hanno ben poca teoria economica a loro supporto, se non addirittura nessuna teoria, o, peggio ancora, teoria incoerente.

Tutto ciò nulla toglie, tuttavia, nè all'aspirazione ideale degli econometristi, nè ai loro sforzi di matematizzare, uniti alla effettiva quantificazione dei fenomeni economici. Occorre inoltre riconoscere la notevole forza propulsiva insita nella convinzione - che risale a Petty, ma che ha avuto esplicita espressione solo negli anni venti del Novecento - che l'economia possa, mediante l'effettiva quantificazione e misurazione dei fenomeni economici, diventare una scienza.

È con questo proposito e con una notevole carica di entusiasmo che, nel dicembre 1930, a Cleveland (Ohio) si tenne la riunione costitutiva della Società Econometrica Internazionale. Lo statuto della Società porta la firma di R. Frisch (norvegese), F. Mill (americano), C. Roos (americano), ai quali venne dato il mandato di stenderne il testo definitivo dopo le discussioni che ebbero luogo in una specie di assemblea costituente.

C'erano tra i soci fondatori tutti i più famosi economisti del mondo, compresi Fisher, Schumpeter e Keynes.

L'organo ufficiale della Società - la rivista ‟Econometrica" - iniziò le pubblicazioni nel 1933 con Frisch come direttore e Fisher come presidente. Nel comitato direttivo originario, composto da otto studiosi, c'era anche l'italiano L. Amoroso dell'Università di Roma.

La rivista ‟Econometrica", divenuta recentemente bimestrale, continua tutt'oggi le sue pubblicazioni, molto accresciuta di articoli e di pagine annualmente pubblicate; i membri della Società Econometrica Internazionale, che erano 163 nel 1931, sono aumentati a 5.823 nel 1983. Ma soprattutto è aumentato nel frattempo il numero delle indagini econometriche pubblicate, non solo nella rivista ‟Econometrica", ma in tutte le riviste di economia, dovunque queste si pubblichino.

Quando una nuova disciplina raggiunge un grado di assestamento tale da garantire un soddisfacente consenso sui problemi principali, l'avvenimento è subito segnalato dall'apparire di libri di testo sull'argomento. Per l'econometria ciò è avvenuto nei primi anni cinquanta, con alcuni ottimi manuali, alcuni dei quali (v. Tintner, 1952; v. Klein, 1953) sono rimasti a lungo un punto di riferimento obbligato per l'insegnamento della disciplina. Un decennio più tardi una seconda generazione di libri di testo ha dato all'econometria sostanzialmente il suo volto attuale (v. Johnston, 1963; v. Malinvaud, 1964; v. Goldberger, 1964). Successivamente nuovi libri di testo hanno continuato ad apparire con la diffusione dell'insegnamento in tutte le maggiori università. Si segnalano qui soltanto alcuni fra i più notevoli (v. Theil, 1971; v. Zellner, 1971; v. Intriligator, 1978).

4. I maggiori centri econometrici

Una rassegna degli sviluppi degli studi econometrici, dalla fondazione della Società Econometrica Internazionale a oggi (1984), richiederebbe molto spazio, anche perché l'interesse per le indagini econometriche ha ormai valicato i confini accademici ed è penetrato nei centri di ricerca più direttamente legati al mondo produttivo, come gli uffici studi e ricerche delle grandi imprese, delle banche e di altre istituzioni finanziarie, degli organismi statali e internazionali. Sarà tuttavia utile menzionare almeno alcuni dei principali centri di ricerca che hanno maggiormente contribuito a questi sviluppi.

Intorno agli stessi fondatori della rivista ‟Econometrica" nacque, negli stessi anni, una fondazione per lo sviluppo delle ricerche econometriche, la Cowles Commission, dal nome del principale finanziatore, A. Cowles. Dapprima associata all'Università di Chicago e dal 1955 a quella di Yale, la Cowles Commission ha costituito all'inizio il punto d'incontro privilegiato fra gli studiosi americani ed europei, che hanno pubblicato nelle monografie della fondazione i loro principali lavori.

Successivamente, i centri si sono sviluppati un po' ovunque. Si ricorderà qui, per gli Stati Uniti d'America, la Brooking Institution a Washington e la Wharton School a Filadelfia, dove un folto gruppo di economisti ha sviluppato le tecniche di costruzione e di utilizzazione dei grandi modelli econometrici (con centinaia di equazioni) delle economie nazionali. Queste ricerche hanno rappresentato la naturale continuazione degli studi pionieristici iniziati negli anni trenta dall'olandese J. Tinbergen (v. i contributi del 1939), direttore del Central Planning Bureau dell'Aia. In Europa, tra i maggiori centri econometrici si possono annoverare il Dipartimento di Economia Applicata dell'Università di Cambridge e la London School of Economics, in Inghilterra; il Center of Operations Research and Econometrics (CORE) dell'Università Cattolica di Lovanio, in Belgio; il Dipartimento di econometria dell'Università di Ginevra; l'Institut National de Statistique et d'Études Économiques (INSEE) di Parigi.

In Italia l'avvio degli studi econometrici è stato più lento, ma dal 1964, data in cui venne istituita la prima cattedra italiana di econometria (all'Università Cattolica del Sacro Cuore di Milano), gli sviluppi sono stati rapidissimi, sia nelle università sia negli uffici studi e ricerche delle grandi istituzioni del mondo bancario e produttivo.

5. L'econometria come disciplina fra economia e statistica

Il contenuto effettivo della maggior parte delle ricerche econometriche è andato restringendosi col trascorrere del tempo.

Nella mente dei fondatori della Società Econometrica Internazionale era molto più forte l'intento di trasformare l'economia in una scienza piuttosto che quello di creare una nuova disciplina che si occupasse specificamente della quantificazione e della misurazione dei fenomeni economici. Tale intento rifletteva molto bene lo spirito positivistico prevalente in quel tempo (ricordiamo che il Circolo di Vienna, nell'agosto 1929, aveva propugnato una rifondazione dello studio delle scienze - comprese quelle sociali - lungo linee molto simili a quelle espresse nello statuto ricordato in precedenza). Successivamente, però, le stesse discussioni filosofiche avevano generato nuovi sviluppi metodologici che, rifiutando una visione meccanicistica dell'unità del metodo scientifico, propugnavano un adattamento della metodologia alle singole discipline. Anche per l'econometria quindi uno sviluppo autonomo veniva delineandosi come tentativo, per molti aspetti pionieristico, di elaborare metodologie specifiche per dati non sperimentali, dati cioè che non sono, né possono essere considerati, ricavati da un esperimento controllato in laboratorio (v. Wold, 1969).

Nella pratica l'econometria ha assunto un senso più ristretto di quello originale, come disciplina che si occupa della quantificazione per la misurazione dei fenomeni economici. Con ciò si intende affermare che, data una teoria economica, ci si occupa, in primo luogo, dei procedimenti per formulare un modello che sia sufficientemente aderente alla teoria per poterla rappresentare in modo adeguato, e sufficientemente semplice per poter essere confrontato con i dati osservati. In secondo luogo ci si occupa di suggerire e, ove non esistano, di costruire i metodi statistici appropriati per la stima dei parametri e per l'accettazione o il rifiuto del modello teorico di partenza sulla base dei dati disponibili (v. statistica). Contributo essenziale nella costruzione del modello, rispetto alla teoria economica, è l'introduzione di variabili probabilistiche, nel caso che la teoria economica non le preveda, oppure la quantificazione in termini operativi degli elementi probabilistici già presenti nella teoria economica, nel caso in cui questa sia formulata come spiegazione del comportamento di operatori che prendono decisioni in condizioni di incertezza. Contributo ulteriore, rispetto alla metodologia statistica, è l'elaborazione, quando necessario, di metodi di stima appropriati ai dati economici disponibili.

Si può illustrare quanto detto con un esempio classico: quello del mercato di un bene in cui si osserva in ogni periodo t la quantità scambiata _tq al prezzo p_t.

Costruire un modello per descrivere, spiegare e prevedere un insieme di fenomeni che interagiscono fra loro (come in questo caso la quantità e il prezzo di un certo bene) significa presupporre l'esistenza di una ‛struttura' che si vuole individuare mediante il ricorso ai dati osservati. La struttura sottostante è rappresentata, in questo caso, dalle due curve di domanda e di offerta del bene, mentre il loro punto di intersezione individua i valori osservati delle due variabili p_t e q_t. Dall'osservazione dei soli punti di intersezione non è evidentemente possibile individuare separatamente le due curve: in termini tecnici ciò viene espresso dicendo che non è possibile ‛identificare' la struttura sottostante a partire dalle variabili osservate. La teoria economica afferma che la quantità domandata qt^D è funzione decrescente del prezzo, mentre la quantità offerta qt^O è funzione crescente del prezzo. La condizione di equilibrio del mercato è che la domanda eguagli l'offerta. Il modello econometrico specifica una forma funzionale per tali relazioni (per esempio la forma lineare) e definisce due variabili probabilistiche (u_1t e u_2t) che riassumono gli effetti di carattere casuale (non sistematico):

Ora si può vedere che i valori dei parametri a, b, e, d (che si suppongono tutti positivi) non possono essere determinati statisticamente disponendo solo di osservazioni su p_t e q_t (a meno di introdurre vincoli complessi - e in generale non realistici - sulla distribuzione congiunta di probabilità di u_1t e u_2t). In altre parole non potremmo individuare la struttura, pur se abbiamo potuto scrivere la ‛forma strutturale' del modello, anche se disponessimo di una serie infinita di osservazioni su p_t e q_t. Possiamo però calcolare i parametri della cosiddetta ‛forma ridotta' del modello, che si ottiene risolvendo rispetto a p_t e q_t:

dove le nuove variabili casuali sono una combinazione lineare di quelle della forma strutturale:

e

,

mentre i parametri sono una combinazione non lineare dei parametri precedenti:

Definite le usuali ipotesi sulla distribuzione di probabilità delle variabili casuali v_1t e v_2t, possiamo - con gli usuali metodi forniti dalla statistica - procedere alla stima dei parametri π₁ e π₂ e quindi dei valori attesi di p_t e q_t, che costituiscono in tal caso una previsione del valore di p_t e q_t che ci si può aspettare nel prossimo periodo. Dalle caratteristiche delle distribuzioni di probabilità di v_1t e v_2t si può inoltre ricavare una misura degli errori che si possono commettere in tale previsione.

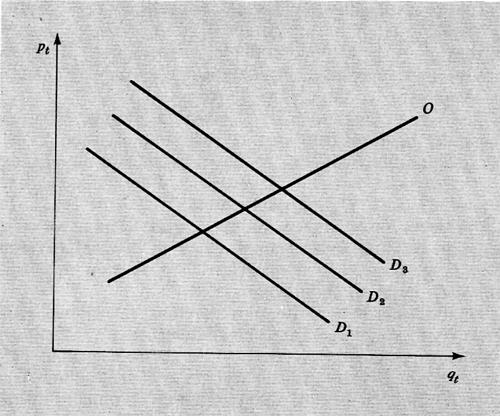
Il nostro esempio ci consente di procedere oltre. Supponiamo di aver commesso un ‛errore di specificazione' nella costruzione del modello, consistente, per esempio, nell'aver omesso una variabile rilevante dal punto di vista della teoria economica. Per esempio, la teoria economica sostiene che la quantità domandata di un bene dipende, oltre che dal prezzo, anche dal reddito dei consumatori, Y_t. Possiamo, ora, considerare diverse funzioni di domanda D₁, D₂, D₃, ..., una per ogni osservato livello di reddito Y₁, Y₂, Y₃, ... . A differenza del caso precedente, siamo ora in grado di ‛identificare' la funzione di offerta tramite i suoi punti di intersezione con le diverse funzioni di domanda.

In modo simmetrico, supponendo per esempio che si tratti di un bene agricolo, l'offerta può dipendere, oltre che dal prezzo, da contributi pubblici ai produttori in ogni particolare anno, Z_t. Avremo in tal caso più funzioni di offerta in corrispondenza di vari livelli di contributi, che anche qui ci permettono di ‛identificare' la funzione di domanda. Le due variabili Y_t e Z_t sono dette variabili ‛esogene', in quanto determinate all'esterno del mercato di cui stiamo descrivendo il comportamento, mentre p_t e q_t vengono dette variabili ‛endogene'.

Dal punto di vista statistico tale nuova situazione corrisponde alla possibilità di scomporre i due residui originali u_1t e u_2t in due componenti indipendenti: u_1t = Y_t + e_1t e u_2t = Z_t + e_2t, dove e_1t, e_2t sono due variabili puramente casuali se non sono stati commessi altri errori di specificazione. Errori di questo tipo possono tuttavia essere individuati con metodologie statistiche di verifica delle ipotesi sulla casualità dei residui (v. sotto).

Se il modello viene ampliato per descrivere situazioni più complesse, alcune variabili esogene possono a loro volta diventare endogene. Si supponga, per esempio, che il reddito Y_t sia determinato da un semplice schema keynesiano:

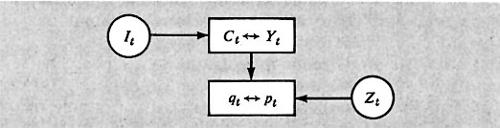
dove C_t è il consumo aggregato di tutte le famiglie e I_t è il livello di spesa autonoma in investimenti. La prima delle due nuove equazioni è la semplificazione lineare della funzione keynesiana del consumo che descrive il comportamento aggregato dei consumatori; la seconda è la condizione keynesiana di equilibrio in economia chiusa. Lo schema del modello così ottenuto può essere illustrato nel modo seguente:

dove nei cerchi sono indicate le nuove variabili esogene e nei rettangoli le relazioni simultanee fra le variabili endogene. Il consumo e il reddito che si determinano a livello macroeconomico hanno un'influenza che possiamo chiamare causale sulle quantità scambiate di un singolo bene, perché l'influenza inversa può essere considerata, in prima approssimazione, trascurabile. Uno schema di questo tipo viene detto ‛causale' o ‛recursivo', per distinguerlo dal caso di un modello ‛simultaneo' o ‛interdipendente', in cui tutte le variabili endogene del modello vengono determinate simultaneamente e simmetricamente fra loro (come avviene all'interno di ciascuno dei due rettangoli). È evidente che le funzioni considerate sono state tratte, seppure in modo estremamente semplificato, da una teoria economica, ma non rappresentano tutte le relazioni della teoria. Se pensassimo di estendere il modello a tutte le relazioni di una teoria economica, il fatto di trovare uno schema recursivo oppure uno schema simultaneo può essere rilevante dal punto di vista dell'interpretazione della realtà. Pasinetti (v., 1965), per esempio, ha sostenuto che il modello della teoria economica marginalistica (neoclassica) è interdipendente, mentre il modello della teoria economica keynesiana è recursivo, in quanto, all'interno di quest'ultima, è possibile stabilire delle catene causali fra variabili o gruppi di variabili del tipo di quelle rappresentate nello schema di cui sopra. A un livello così generale, però, le tecniche econometriche non sono in grado di individuare, in base ai dati disponibili, quale teoria sia una migliore descrizione della realtà, e ciò non solo per inadeguatezza delle metodologie esistenti, ma anche perché, sovente, le teorie stesse si propongono come visioni alternative di una realtà complessa.

La distinzione fra modelli recursivi (o causali) e modelli interdipendenti è stata a lungo al centro dell'attenzione degli econometristi. In particolare due autori, R. Strotz e H. Wold (v., 1960), hanno sostenuto che un modello interdipendente è o un'approssimazione di un modello recursivo o una descrizione del suo stato di equilibrio. Se il modello viene scritto in modo interdipendente e non recursivo - essi hanno sostenuto - ciò è a causa della mancanza di dati sufficientemente frequenti nel tempo. Ciò significa che la descrizione della realtà viene intesa come la ricerca di relazioni di causa-effetto che richiedono un certo periodo di tempo per la loro esplicazione. Solo se i dati disponibili sono rilevati a intervalli più lunghi di tale periodo ritroviamo delle relazioni ‛simultanee'.

Vi è inoltre un importante aspetto statistico del problema. I modelli (o i gruppi di equazioni all'interno di un modello) interdipendenti non possono essere stimati con il tradizionale metodo dei minimi quadrati, in quanto si commetterebbe un errore sistematico (cioè non eliminabile neppure aumentando indefinitamente il numero delle osservazioni disponibili) detto ‛errore di simultaneità' (v. statistica). Proprio l'individuazione di metodi di stima appropriati per tali situazioni di interdipendenza o simultaneità rappresenta uno dei maggiori contributi forniti dallo sviluppo degli studi econometrici (v. Haavelmo, 1944; v. Koopmans, 1950; v. Basmann, 1957; v. Theil, 1958; v. Zellner e Theil, 1962).

6. Dibattiti e problemi irrisolti

Si consideri ora uno dei problemi principali dell'econometria, quello di cercare di risalire dalla conoscenza della distribuzione di probabilità di un gruppo di variabili endogene osservate (subordinatamente ai valori assunti da un gruppo di variabili esogene) a una sottostante, incognita, struttura di relazioni di comportamento che legano le variabili fra loro. Ci si può chiedere: perché, e quando, è importante la conoscenza di tale struttura? Si risponderà con due esemplificazioni. Si consideri il seguente modello nella forma strutturale:

dove le variabili hanno lo stesso significato del capitolo precedente, con la differenza che al posto del reddito è stato inserito il ‛reddito disponibile' (y_t − b_ty_t), dove b_t è l'aliquota di imposta sul reddito. La sua forma ridotta sarà:

dove i parametri π_ij e le nuove variabili casuali v_it della forma ridotta vengono definiti implicitamente, analogamente al caso del capitolo precedente, come funzioni, rispettivamente, dei parametri e delle variabili casuali della forma strutturale. Un problema che ci si può porre è quello di prevedere i valori futuri delle variabili endogene, una volta assegnati certi valori alle variabili esogene. Ora, se la struttura non cambia nel tempo, la conoscenza dei valori stimati di π_ij sarà sufficiente a tale scopo. Ma se abbiamo motivi per aspettarci che cambi e se, per esempio, ci si aspetta che cambi la propensione dei consumatori a spendere il proprio reddito nell'acquisto di quel bene, dobbiamo aspettarci anche una variazione del parametro a₃ che assumerà, diciamo, il valore a₃ + k. La previsione corretta di p_t mediante la forma ridotta si otterrebbe, ora, solo assegnando al parametro π₁₂ il valore

È chiaro che questa modifica si può fare solo se conosciamo la forma strutturale.

Supponiamo, ora, un altro caso in cui osserviamo una variazione non desiderata della distribuzione di probabilità di p_t e q_t, cioè del valore dei parametri π_ij, e supponiamo di voler capire l'origine di tale variazione, per esempio, per poter intervenire e ristabilire la situazione iniziale. È chiaro che, se la variazione proviene dal lato della domanda, si dovrà intervenire sul reddito dei consumatori (per esempio sul parametro b_t), ma, se proviene dal lato dell'offerta, l'intervento dovrà avvenire sui contributi ai produttori (cioè sulla variabile z_t). Di nuovo diventa necessaria la conoscenza della struttura.

Questi problemi sono stati chiaramente espressi da Marschak (v., 1953) e Hurwicz (v., 1962) in due lavori che riassumono numerose ricerche sull'argomento. Nella loro concezione la teoria economica assume un ruolo fondamentale proprio nell'indicare la corretta forma strutturale del modello. In particolare la teoria economica dovrebbe essere in grado di indicare la lista completa delle variabili rilevanti, quali variabili entrano in ciascuna equazione, la distinzione fra variabili endogene e variabili esogene, gli eventuali ritardi con cui certe variabili influiscono su altre, ecc. Tuttavia non vi è mai stato un accordo generale sulla capacità della teoria economica prevalente di rispondere correttamente a tali esigenze, cioè di identificare correttamente delle buone forme strutturali per la costruzione di modelli econometrici. A più riprese si è acceso un dibattito sul peso relativo che hanno la teoria economica e l'analisi statistica. Si è discusso a lungo sulla distinzione fra modelli strutturali basati sulla teoria economica e modelli basati prevalentemente su regolarità empiriche osservate. Questi ultimi sono stati accusati di essere una misurazione priva di teoria (v. Koopmans, 1947; v. Vining, 1949). La versione più recente di questa disputa è fra i difensori del ruolo di una teoria economica che trae sostanzialmente origine dagli schemi keynesiani (L. Klein ne è il maggiore rappresentante in campo econometrico) e i sostenitori della crisi di tale teoria e della sua inferiorità, a fini di previsione, rispetto a modelli più semplificati, ma basati su tecniche statistiche più appropriate (v. Sargent e Sims, 1977).

Accade spesso nella ricerca scientifica che il maggior stimolo allo sviluppo di una teoria o di un gruppo di metodologie venga proprio dalle critiche più radicali a cui le stesse sono sottoposte. Così è stato anche per l'econometria, in risposta a uno scetticismo abbastanza diffuso e mai spento sulla possibilità stessa di adottare tecniche statistiche nell'analisi dei fenomeni economici. Tale scetticismo ha radici lontane. Un esempio illustre è costituito da una famosa critica che J. M. Keynes (v., 1939) rivolse alle tecniche di regressione utilizzate da Tinbergen (v. i contributi del 1939) per lo studio dei cicli economici. L'articolo di Keynes sollevò alcuni problemi di fondo che hanno poi costituito il programma di ricerca di numerosi econometristi.

Per comodità si raggrupperanno qui i maggiori problemi sollevati da questa e da altre dispute in tre grandi categorie.

1. Esistono anzitutto problemi di portata generale che riguardano i fondamenti dello stesso metodo econometrico e che, come tali, non verranno forse mai risolti. Il più importante è costituito dall'incapacità dei metodi econometrici di portare a una scelta tra teorie economiche alternative sulla base del comportamento dei modelli. La difficoltà è qui legata alla natura delle discipline sociali, che preclude la possibilità di esperimenti controllati. Ogni giudizio è basato prevalentemente sulla capacità di previsione, ma ciò ha senso, come abbiamo già accennato, solo se la struttura sulla quale è stato stimato il modello persiste nel tempo. Quando il modello fallisce le previsioni, è difficile decidere se è errata la teoria dalla quale il modello deriva o se è cambiata la struttura (in un modo che può essere contemplato dalla teoria, ma non incorporato nella stima del modello, solo perché quel tipo di variazione non si era verificato nel passato). Strettamente legata a questo problema è la possibilità di distinguere fra semplici correlazioni statistiche e relazioni di causa-effetto fra le variabili. Molti autori sono scettici riguardo al fatto che ciò sia possibile nelle scienze non sperimentali. Quando diciamo, per esempio, che la causa dell'inflazione è stato l'aumento dei salari monetari, vogliamo asserire almeno che, a parità di altre condizioni (ceteris paribus), se tale aumento non ci fosse stato non sarebbero aumentati i prezzi. Ma certo non possiamo effettuare un esperimento di tal tipo, possiamo solo immaginarlo e riprodurlo con uno dei nostri modelli (tecnicamente, possiamo simularlo). La risposta del modello dipenderà però e dalla teoria e dal modo in cui è stato costruito il modello: se la teoria presuppone il legame causale e il modello non lo riproduce, non siamo immediatamente autorizzati a negare tale legame e a respingere la teoria. È necessario indagare sul modo in cui è stato costruito il modello, sulla inadeguatezza dei dati utilizzati, sulla validità delle condizioni ceteris paribus. La possibilità di effettuare tali esperimenti ipotetici (a volte detti controfattuali, in quanto si basano su ipotesi che sappiamo essere contrarie ai fatti realmente accaduti) per studiare l'efficacia degli interventi di politica economica è stata recentemente riconsiderata, dando luogo a una vasta letteratura che ha dedicato la propria attenzione sia a una riconsiderazione della teoria economica, sia al modo di costruire i modelli (v. Sims, 1980).

Un altro problema di carattere generale, cui si è già accennato all'inizio, riguarda la possibilità di ridurre a espressioni quantitative fenomeni che hanno forti componenti psicologiche non misurabili, quali le aspettative o le preferenze dei consumatori, che svolgono un ruolo fondamentale nella teoria economica.

2. Esistono inoltre problemi di carattere più tecnico che sono invece risolvibili e la cui soluzione costituisce anzi il maggiore impegno per la teoria econometrica. A differenza di quelli del gruppo precedente, questi problemi sono stati avviati a soluzione mediante un continuo raffinamento delle metodologie. Si è già accennato a metodi di stima particolari che sono stati studiati per il caso in cui una o più variabili esplicative, in una equazione del modello, dipendano a loro volta dalla variabile dipendente, attraverso altre equazioni. Sono stati sviluppati metodi di verifica delle ipotesi per ricercare se la lista di variabili esplicative considerate sia completa oppure se qualche variabile rilevante sia rimasta nei residui dell'equazione, viziando così di un errore sistematico le stime.

Un'esigenza importante che si è avvertita recentemente è quella di combinare, nella costruzione e nella stima del modello, l'informazione statistica dei dati con altre informazioni, che provengono da una conoscenza precedente del fenomeno. Tali informazioni sono spesso quantificabili in termini di vincoli sui parametri o sulla distribuzione di probabilità dei residui delle equazioni. Le metodologie econometriche per trattare tali problemi hanno recentemente tratto sviluppi interessanti dall'analisi statistica bayesiana.

3. Esistono infine problemi di carattere più specifico, legati a particolari tipi di modelli o a particolari tipi di applicazioni. Spesso viene criticato l'eccessivo ricorso all'ipotesi di linearità dei modelli, adottata per semplificarne la soluzione e la stima. La validità di tali critiche va valutata caso per caso. Si può dire che sono state sviluppate metodologie per modelli non lineari e che i moderni elaboratori elettronici, a elevata capacità e velocità di calcolo, permettono al riguardo l'uso di tecniche di stima, previsione e controllo di tali modelli, che erano un tempo impossibili. Altri problemi sorgono spesso relativamente al trattamento preliminare dei dati utilizzati per le stime. Non sempre i modelli possono essere stimati su dati ‛grezzi', così come questi vengono raccolti dagli istituti di statistica nazionali, o internazionali, e ciò per svariate ragioni: a) i dati raccolti possono non corrispondere esattamente al concetto teorico che si dovrebbe misurare (per esempio: la variazione dei salari dovuta a variazioni nelle condizioni di offerta e domanda nel mercato del lavoro non è tutta quella misurata dai dati, in quanto vi sono meccanismi di adeguamento automatico, quali le indennità di contingenza); b) nei dati vi sono elementi che si devono depurare (quali la stagionalità), perché la loro presenza renderebbe non interpretabili le relazioni statistiche fra le variabili; c) si devono utilizzare i dati osservati per costruire correlati empirici a variabili non direttamente osservabili, quali il reddito considerato permanente dai consumatori o il prodotto potenziale di un'economia.

Un ulteriore problema che va menzionato riguarda la difficoltà di adottare, nei modelli macroeconomici, funzioni di comportamento che in teoria sono state formulate con riferimento a singoli individui. Ciò chiama in causa il cosiddetto problema dell'aggregazione di relazioni microeconomiche per studiare il comportamento di un unico operatore macroeconomico ideale. Questi problemi sono particolarmente rilevanti nella teoria del consumo e in quella degli investimenti, ma non hanno trovato soluzioni veramente soddisfacenti fino a questo momento. Per ciò che è stato fatto, lo studio più completo resta quello di Theil (v., 1954).

7. Problemi rilevanti

Due autori americani, che hanno tentato recentemente di passare in rassegna i problemi che sono attualmente rilevanti per gli studiosi di econometria, hanno curato un'ampia antologia in tre volumi (v. Griliches e Intriligator, 1984). In questa sede si può solo accennare ai principali problemi trattati. Con questo intento, i tre paragrafi seguenti verranno dedicati à tre grandi gruppi di problemi: a) problemi relativi alla costruzione del modello, che riguardano i tentativi di evitare o di scoprire i possibili errori di specificazione; b) problemi relativi alla scelta fra modelli alternativi: un progetto meno ambizioso di quello, difficilmente perseguibile, come si è già accennato, di discriminare tra teorie economiche; c) problemi relativi all'utilizzazione dei modelli, fra i quali assumono particolare rilevanza la previsione e, nel caso della macroeconomia, la valutazione di politiche economiche alternative.

a) Errori di specificazione

Col termine ‛errore di specificazione' si indica qualsiasi divergenza significativa fra le ipotesi sulle quali è basato il modello e le proprietà reali dell'insieme di fenomeni che tale modello intende rappresentare.

Se indichiamo con y_t la variabile che si intende spiegare, con x_t il vettore delle variabili rilevanti per la sua spiegazione, con b il vettore dei parametri incogniti che misurano l'influenza di ciascuna variabile contenuta in x_t su y_t e, infine, con u_t una variabile casuale residuale, si usa scrivere in modo compatto la seguente relazione lineare:

y_t = x_tb + u_t.

A questa espressione, nel caso di discipline non sperimentali come l'econometria, non è possibile applicare immediatamente i metodi classici dell'inferenza statistica, perché questi metodi classici sono basati su un insieme di ipotesi che sono raramente accettabili per i fenomeni economici. Questo insieme di ipotesi, che Leamer (v., 1978) chiama ‛assioma di corretta specificazione', si presenta come segue: a) il gruppo di variabili contenute in x_t deve essere unico, completo, poco numeroso, osservabile e non correlato con u_t; b) u_t deve avere una distribuzione di probabilità nota a meno di un piccolo numero di parametri costanti (media e varianza, in generale); c) b deve essere costante (non dipendere da t).

Nel trattare le deviazioni dall'assioma di corretta specificazione possiamo distinguere due situazioni sostanzialmente differenti: la prima è quella in cui si è consapevoli di commettere un certo errore di specificazione, non evitabile data la natura del problema che si sta considerando, e il problema è pertanto quello di usare le metodologie statistiche appropriate per ridurre al minimo l'influenza di tale errore sui risultati del modello. La seconda situazione è quella in cui si tenta una prima specificazione, la più corretta possibile, del modello e si cerca poi di scoprire se è stato commesso qualche errore di specificazione e quale esso sia analizzando i risultati ottenuti nella stima del modello.

Considereremo alcuni esempi di ambedue le situazioni. Un esempio tipico della prima situazione è quello in cui una variabile, diciamo x_t, è misurata con errore oppure non è osservabile e deve essere approssimata mediante una o più variabili osservabili. Supponiamo di avere l'equazione

y_t = bx_t + u_t

e che la relazione fra la variabile misurata ù_t, e la variabile rilevante x_t sia

ù_t = x_t + v_t,

dove v_t è una variabile casuale. I metodi classici di inferenza (per esempio, il metodo dei minimi quadrati) daranno per l'equazione

y_t = bù_t + e_t

una stima di b affetta da errori sistematici, in quanto l'errore e_t e la variabile ù_t risultano correlati, anche se le variabili x_t, u_t, v_t non lo sono. Infatti

dove e_t = u_t − bv_t. Ne consegue che la covarianza fra ù_t e e_t sarà

Cov(ù_t, e_t) = Cov(x_t + v_t, u_t − bv_t) = − b Var(v_t) ≠ 0.

Il metodo di stima cui si ricorre in tal caso è quello delle variabili strumentali. Tale metodo, che si può far risalire a Reiersøl (v., 1941), consiste nel trovare una variabile che sia correlata con ù_t, ma non correlata con e_t. Si dimostra che in tal caso, se si utilizza ù_t-1, la stima di b sarà

Formula,

che gode di proprietà ottimali.

Un secondo esempio, sempre della prima situazione, riguarda l'assunzione dell'ipotesi di distribuzione normale degli errori u_t, per motivi di convenienza statistica, anche nei casi in cui tale ipotesi non è giustificata dal tipo di dati che si stanno considerando. In tal caso possono essere utilizzati metodi di stima cosiddetti ‛robusti' (v. Huber, 1981), in quanto non perdono le loro proprietà ottimali anche se ci si discosta dalle ipotesi su cui sono basati.

Per quanto riguarda la seconda situazione, il caso più frequente è quello - già considerato nell'esempio delle funzioni di domanda e di offerta - dell'omissione di una o più variabili rilevanti. Sia data l'equazione scritta in termini matriciali:

y = Xb + u,

dove y è il vettore contenente i valori osservati della variabile dipendente, X è la matrice contenente i valori osservati delle variabili esplicative, u è un vettore di variabili casuali non osservabili e b è il vettore dei parametri incogniti da stimare. Dopo aver stimato b con il metodo dei minimi quadrati, ossia b = (X′X)^-1Xy, si definiscono i residui stimati:

û = y − Xb.

Utilizzando tali residui si può costruire una serie di test statistici per verificare singole ipotesi di corretta specificazione. Va precisato che una caratteristica generale di tali test è che, nel caso in cui le ipotesi considerate vengano rifiutate, non risulta definita in modo preciso l'ipotesi alternativa da accettare. In altre parole, la procedura può indicare che l'ipotesi considerata deve essere respinta, ma non indica la strada per correggere l'errore di specificazione. Test specifici sono stati però costruiti per ipotesi alternative varie: per esempio, per l'ipotesi alternativa che b vari nel tempo, che la varianza di u_t non sia costante, che i residui u_t, siano correlati con i propri valori passati (v. Durbin e Watson, 1950).

b) Scelta fra modelli alternativi

Una situazione che spesso si presenta al ricercatore è quella in cui più di un modello costruito per la spiegazione di un certo insieme di fenomeni soddisfa i requisiti di accettabilità delineati nel paragrafo precedente. Si pone, in tal caso, un problema di scelta fra modelli alternativi.

Va precisato, prima di procedere, che un modello econometrico è una rappresentazione semplificata e formalizzata di una parte di una teoria economica. Se i due modelli alternativi fra cui dobbiamo effettuare una scelta si riferiscono a due diverse teorie economiche, in generale non sarà vero che il rifiuto di un modello significhi il rifiuto della teoria dalla quale il modello è stato ricavato. Molte possibili spiegazioni rimangono aperte: si possono mettere in discussione i criteri statistici usati per la scelta del modello, vi possono essere revisioni o incertezze nei dati utilizzati, si può formulare una spiegazione più elaborata all'interno della teoria, che renda conto del rifiuto di quel particolare modello, e così via.

L'impostazione attuale del problema della scelta fra modelli fa riferimento in gran parte al metodo della massima verosimiglianza. Supponiamo di avere due modelli M₁ e M₂ per spiegare la stessa variabile Y sulla base di due diversi insiemi di variabili X₍₁₎ e X₍₂₎:

La variabile casuale Y ha una sua distribuzione di probabilità p(Y; b_(i)). Se abbiamo T osservazioni di Y, la distribuzione di probabilità congiunta di tutti i valori osservati è una funzione dei parametri incogniti b_(i) e viene detta ‛funzione di verosimiglianza':

L(b_(i)) = C p(y₁, ..., y_T; b_(i)),

dove C è una costante che può dipendere da y_t. Il principio della massima verosimiglianza afferma che una corretta inferenza statistica deve essere coerente con l'assunto che la migliore spiegazione dell'insieme di dati y₁, ... , y_T è fornita da quel valore di b_(i) che rende massima la funzione di verosimiglianza: max L(b_(i)). Il significato è che la massimizzazione ci porta a scegliere quel valore di b_(i), che indichiamo con á_(i), in corrispondenza del quale l'insieme dei valori osservati risulta il più probabile. Esso è detto lo stimatore di massima verosimiglianza di b_(i). Se il modello M₁ può essere considerato come caso particolare di M₂, ottenuto vincolando certi parametri ad assumere particolari valori, allora la scelta fra i due modelli si può effettuare utilizzando il rapporto di verosimiglianza. Si calcolano cioè i massimi delle due funzioni di verosimiglianza L₁ = L(á₍₁₎) e L₂ = L(á₍₂₎) e si costruisce il rapporto R = L₁/L₂, che (essendo M₁ un caso particolare di M₂) risulta essere ≤ 1. Ora quando è il modello M₂ a spiegare in modo appropriato i dati, il valore R tende a essere piccolo; si tratta allora di determinare un valore R_c tale che se R 〈 R_c si rifiuta il modello M₁. Si può dimostrare che tale test gode di certe proprietà: per esempio, all'aumentare della dimensione del campione, la probabilità di rifiutare M₁, quando il modello migliore è M₂, tende all'unità.

Nella teoria statistica classica fin qui considerata i parametri b_(i) sono ritenuti delle costanti. Una teoria alternativa, qualificata come bayesiana (v. Zellner, 1980), li considera delle variabili casuali che posseggono una loro funzione di densità di probabilità che deve essere definita a priori, prima della considerazione dei modelli. L'esistenza di tale informazione a priori influenza la successiva scelta fra i modelli, nel senso che ogni singolo modello deve essere giudicato sia in base a un insieme di valori dei parametri, che sia verosimile a priori, sia in base a quei valori che vengono indicati come più probabili dal campione dei dati. Si adotta in tal caso un criterio simile a R di cui sopra, come rapporto fra le probabilità a posteriori dei due modelli, le quali a loro volta sono definite come il prodotto fra le probabilità a priori e le rispettive funzioni di verosimiglianza:

Un vantaggio teorico di tale approccio è che il criterio R′ (a differenza di R) può essere utilizzato per due modelli qualsiasi e non soltanto quando il primo è un caso particolare del secondo. Benché più attraente dal punto di vista teorico, anche perché permette di incorporare nel giudizio sui modelli elementi già in possesso del ricercatore, ma che sono estranei al campione di dati che sta considerando, la metodologia bayesiana ha lo svantaggio, dal punto di vista applicativo, che il calcolo di R′ è in generale molto più complesso che non quello di R. Per tale motivo le sue applicazioni sono ancora relativamente ridotte.

c) Uso dei modelli per la previsione e la valutazione di politiche economiche

Quando un modello econometrico viene ritenuto, in prima approssimazione, correttamente specificato e quando, con un appropriato metodo di stima, si sono ottenuti valori numerici per i suoi parametri, il modello stesso può essere utilizzato per effettuare delle simulazioni, normalmente per mezzo di un elaboratore elettronico. Se le equazioni del modello sono una buona descrizione del comportamento degli operatori economici, la soluzione per le variabili endogene, data dal modello nel periodo storico sul quale sono state calcolate le stime dei parametri, dovrebbe essere ‛vicina' ai valori osservati per le stesse variabili. Una forma strutturale tipica di un modello econometrico lineare e dinamico è la seguente:

A₀Y_t + A₁Y_t-1 + BX_t = U_t,

dove Y_t è il vettore delle variabili endogene, X_t il vettore delle variabili esogene, A₀ e A₁ sono, rispettivamente, le matrici (quadrate) dei parametri delle variabili endogene contemporanee e ritardate di un periodo, B è la matrice (rettangolare) dei parametri delle variabili esogene e, infine, U_t è un vettore di variabili casuali non osservabili. La soluzione si otterrà tramite la forma ridotta stimata (Û_t = 0):

,

dove Â₀, Â₁, Á sono le matrici dei parametri stimati e ŷ_t sono i valori di Y_t calcolati dal modello. La soluzione richiede che la matrice A₀ sia di rango pieno e pertanto esista la sua inversa A0^-1. Se il modello non è lineare nelle variabili Y_t si dovranno invece usare dei metodi iterativi (v. Goldfeld e Quandt, 1972).

L'uso delle simulazioni, per una disciplina non sperimentale come l'econometria, sostituisce l'uso di esperimenti controllati in laboratorio (v. Wold, 1969). Le simulazioni vengono effettuate dapprima sul periodo storico per il quale sono noti i valori di X_t, allo scopo di verificare l'adeguatezza del modello nel ricostruire l'andamento del sistema economico. Quindi, allorché il modello supera tutte le verifiche, si può procedere a utilizzarlo per calcolare i valori di Y_t al di fuori del periodo che è servito per stimare i parametri:

Formula.

Possiamo distinguere fra una previsione ‛pura', in cui i valori Á_T+j sono estrapolazioni per il futuro delle variabili X_t, con metodi estranei alla costruzione del modello (v. anche statistica), e una previsione ‛ipotetica', in cui alle X_T+j vengono assegnati valori alternativi secondo particolari criteri, con lo scopo di valutare possibili effetti di diversi scenari di politica economica (v. Duesenberry e altri, 1960).

In realtà l'uso di un modello econometrico (composto spesso da centinaia di equazioni) in tali situazioni non è così meccanico come potrebbe sembrare dalla descrizione precedente. Come più volte sottolineato (v. Klein, 1947; v. Klein e Young, 1980), tale uso richiede la considerazione di elementi di informazione estranei al modello, di natura sia quantitativa che qualitativa, relativi all'effettivo funzionamento del sistema economico. Ciò comporta anche l'estrema difficoltà di valutare i risultati di tale attività: ogni nuova previsione, infatti, non è una correzione della precedente, ma una nuova valutazione basata su informazioni a volte discordanti da quelle precedenti.

Un confronto fatto a posteriori delle previsioni con i valori effettivamente realizzati di Y_T+j è significativo nel caso delle previsioni ‛pure', ma ha poco senso per le previsioni ‛ipotetiche', in quanto i valori di YE_T+j erano stati calcolati sulla base di un insieme di informazioni diverso da quello poi realizzatosi.

Un altro possibile uso di un modello econometrico relativo alla valutazione della politica economica è il cosiddetto approccio di Tinbergen (v., 1956), in cui si suppone che esistano valori desiderati per certe variabili endogene y*_i,T+j, dette variabili ‛obiettivo', e che ci siano certe variabili, dette variabili ‛strumento', sotto il diretto controllo dell'autorità pubblica, manovrando le quali si può cercare di raggiungere gli obiettivi. Perché vi sia una soluzione del problema, il numero delle variabili strumento deve essere maggiore o tutt'al più uguale a quello delle variabili obiettivo. Un ulteriore sviluppo di tale approccio (v. Theil, 1971) è l'uso nel modello di tecniche di controllo ottimale, in cui definendo una certa funzione del benessere sociale in termini di obiettivi desiderabili (riguardanti, per esempio, il tasso di disoccupazione o il disavanzo della bilancia dei pagamenti) si definiscono dei tracciati ottimali per certe variabili endogene, da raggiungere con l'uso di certi strumenti di politica economica. In questo secondo caso, rispetto al primo, viene privilegiato l'aspetto dinamico del problema e diventa rilevante la lunghezza del periodo necessario per raggiungere i valori desiderati delle variabili obiettivo.

L'uso di modelli econometrici per la previsione e la valutazione della politica economica è oggi molto diffuso nonostante taluni insuccessi e le molte critiche, cui si è fatto cenno. Comunque la ricerca è in corso e promette sempre nuovi sviluppi.

bibliografia

Basmann, L.R., A generalized classical method of linear estimation of coefficients in a structural equation, in ‟Econometrica", 1957, XXV, pp. 77-83.

Contini, B., Introduzione all'econometria, Bologna 1973.

Duesenberry, J.S., Eckstein, O., Fromm, G., A simulation of the United States economy in recession, in ‟Econometrica", 1960, XXVIII, pp. 749-809.

Durbin, J., Watson, G. S., Testing for serial correlation in least squares regression, in ‟Biometrika", 1950, XXXVII, pp. 1-19; 1951, XXXVIII, pp. 157-178.

Frisch, R., Editorial, in ‟Econometrica", 1933, I, pp. 1-4.

Goldberger, . S., Econometric theory, New York 1964.

Goldfeld, S. M., Quandt, R.E., Nonlinear methods in econometrics, Amsterdam 1972.

Griliches, Z., Intriligator, M.D. (a cura di), Handbook of econometrics, 3 voll., Amsterdam 1984.

Haavelmo, T., The probability approach in econometrics, in ‟Econometrica", 1944, XII, suppl., pp. 1-118.

Huber, P. J., Robust statistics, New York 1981.

Hurwicz, L., On the structural form of interdependent systems, in Logic methodology and philosophy of science (a cura di E. Nagel, P. Suppes, A. Tarski), Stanford 1962, pp. 232-239.

Intriligator, M.D., Econometric models, techniques, and applications, Amsterdam 1978.

Johnston, J., Econometric methods, New York 1963 (tr. it.: Econometrica, Milano 1966).

Keynes, J. M., Professor Tinbergen's method, in ‟The economic journal", 1939, IL, pp. 558-568.

Klein, L.R., The use of econometric model as a guide to economic policy, in ‟Econometrica", 1947, XV, pp. 111-151.

Klein, L.R., A textbook of econometrics, Evanston 1953 (tr. it.: Econometria, Milano 1975).

Klein, L.R., An introduction to econometrics, Englewood Cliffs 1962 (tr. it.: Introduzione all'econometria, Milano 1966).

Klein, L.R., Young, R.M., An introduction to economtric forecasting and forecasting models, Lexington, Mass., 1980.

Koopmans, T.C., Measurements without theory, in ‟Review of economics and statistics", 1947, XXIX, pp. 161-172.

Koopmans, T.C. (a cura di), Statistical inference in dynamic economic models, New York 1950.

Leamer, E.E., Specification searches, New York 1978.

Leontief, W.W., The structure of American economy 1919-1929, Cambridge, Mass., 1941.

Malinvaud, E., Méthodes statistiques de l'économétrie, Paris 1964 (tr. it.: Metodi statistici dell'econometria, Torino 1971).

Marschak, J., Economic measurement for policy and prediction, in Studies in econometric methods (a cura di W. C. Hood e T.C. Koopmans), New Haven 1953, pp. 1-26.

Pasinetti, L., Casualità e interdipendenza nell'analisi econometrica e nella teoria economica, in Annali dell'Università Cattolica del Sacro Cuore, Milano 1965, pp. 231-250.

Reiersol, O., Confluence analysis by means of lag moments and other methods of confluence analysis, in ‟Econometrica", 1941, IX, pp. 1-24.

Sargent, J., Sims, C., Business cycle modeling withouth pretending to have too much a priori economic theory, in New methods in business cycle research (a cura di C. Sims), Minneapolis 1977, pp. 45-110.

Sims, C.A., Macroeconomics and reality, in ‟Econometrica", 1980, IIL, pp. 1-48.

Strotz, R. H., Wold, H. O., Recursive vs nonrecursive systems: an attempt at synthesis, in ‟Econometrica", 1960, XXVIII, pp. 417-427.

Theil, H., Linear aggregation of economic relations, Amsterdam 1954.

Theil, H., Economic forecasts and policy, Amsterdam 1958.

Theil, H., Principles of econometrics, New York-Amsterdam 1971 (tr.it.: Principi di econometria, Milano 1977).

Tinbergen, J., Statistical testing of business cicle theories, vol. I, A method and its application to investment activity, Genève 1939.

Tinbergen, J., Statistical testing of business cicle theories, vol. II, Business cycle in the United States of America 1919-1939, Genève 1939.

Tinbergen, J., Economic policy: principles and design, Amsterdam 1956.

Tintner, G., Econometrics, New York 1952.

Vining, R., Koopmans on the choice of variables to be studied and of measurement, in ‟Review of economics and statistics", 1949, XXXI, pp. 77-86.

Wold, H. O., Econometrics as pioneering in non-experimental model building, in ‟Econometrica", 1969, XXXVII, pp. 369-381.

Wonnacott, R. J., Wonnacott, T. H., Econometrics, New York 1970 (tr. it.: Trattato di econometrica, Milano 1974).

Zellner, A., An introduction to Bayesian inference in econometrics, New York 1971.

Zellner, A. (a cura di), Bayesian analysis in econometrics and statistics, Amsterdam 1980.

Zellner, A., Theil, H., Three-stage least squares: simultaneous estimation of simultaneous equations, in ‟Econometrica", 1962, XXX, pp. 54-78.