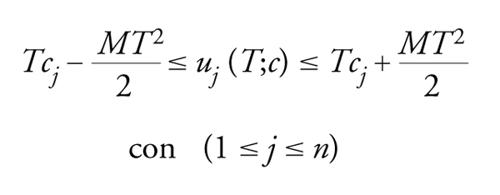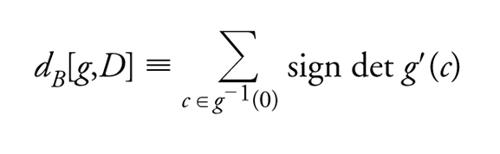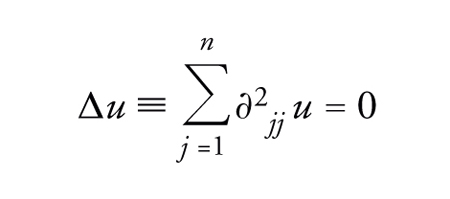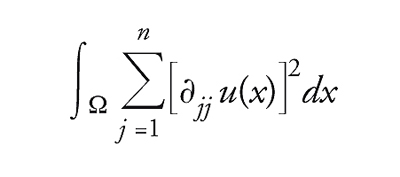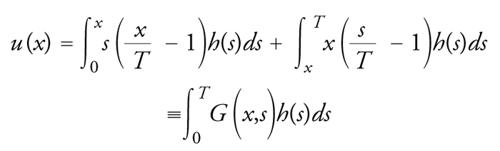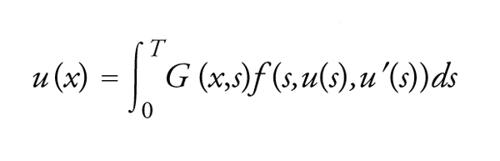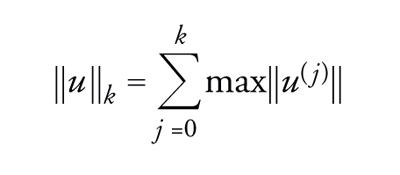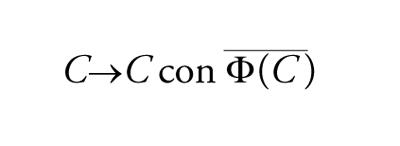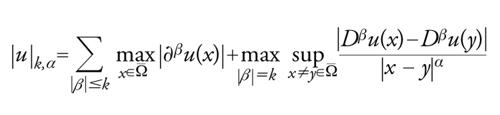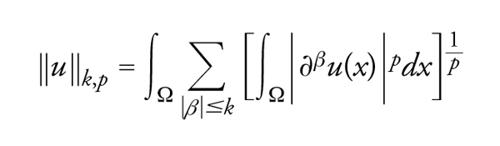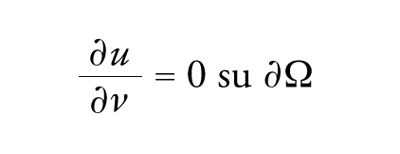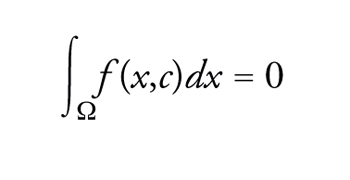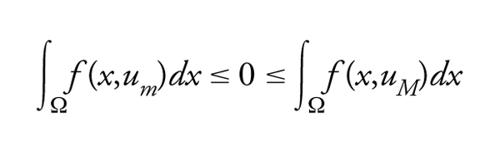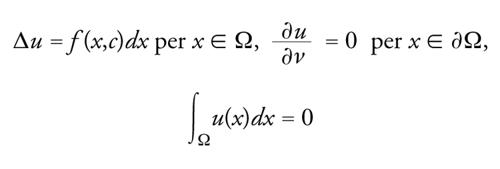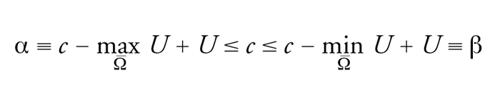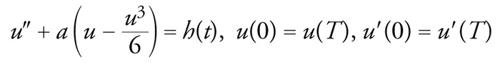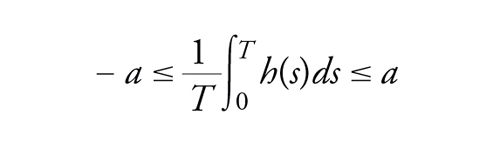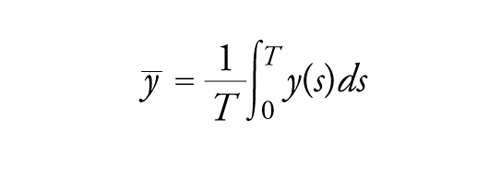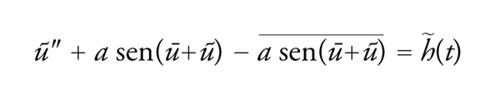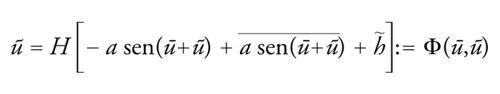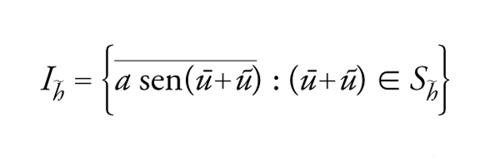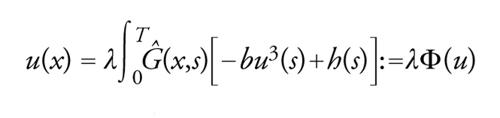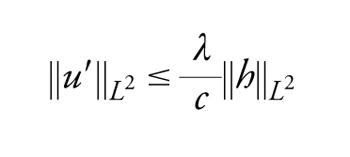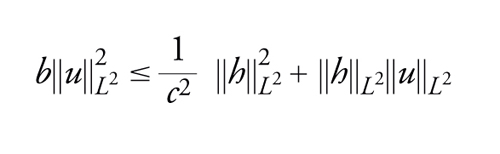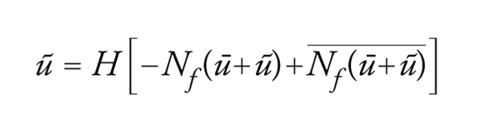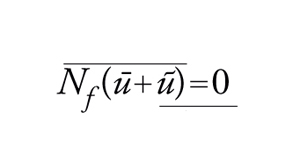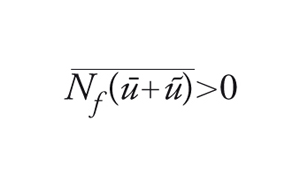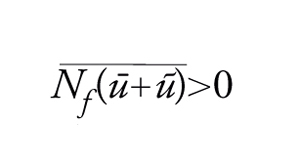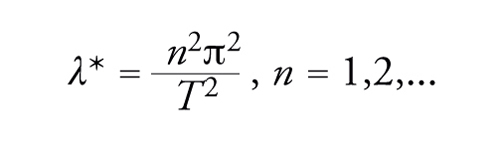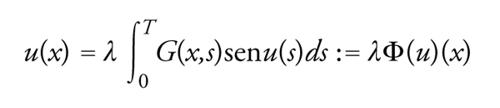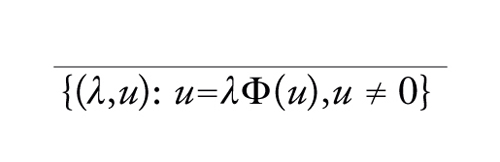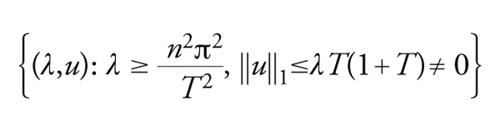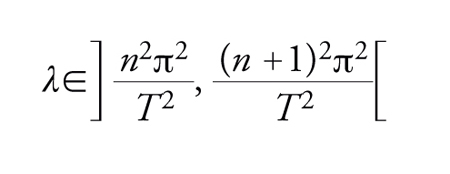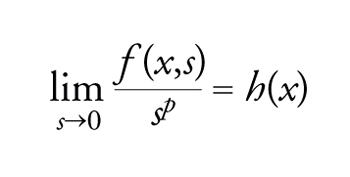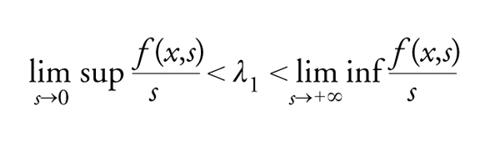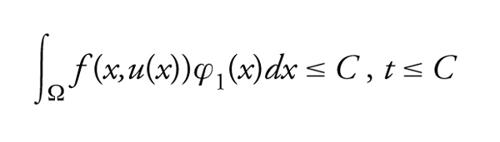Equazioni differenziali: problemi non lineari

Equazioni differenziali: problemi non lineari

La modellizzazione di molti problemi fisici porta alla ricerca di soluzioni di equazioni differenziali di secondo ordine, ordinarie o alle derivate parziali di tipo ellittico, che assumono valori dati sul bordo di un dominio limitato (un intervallo, nel caso ordinario) dello spazio della variabile indipendente (problema di Dirichlet). Un'altra questione di notevole importanza, per un'equazione differenziale ordinaria di secondo ordine, riguarda la ricerca di soluzioni che, insieme alla loro derivata prima, assumano lo stesso valore sia all'origine, sia all'estremità di un dato intervallo (problema periodico).

Nel caso di un'equazione differenziale ordinaria, la cui soluzione del corrispondente problema del valore iniziale esiste ed è unica sull'intervallo dato, quei problemi possono essere ridotti rispettivamente a trovare uno zero di una funzione reale di una variabile reale (non esplicitamente nota) o uno zero comune di due funzioni di due variabili reali. Ciò si può ottenere usando nel primo caso il teorema di esistenza degli zeri di Bolzano (shooting method) ma, nel secondo caso, richiede più sofisticati strumenti topologici, come il grado di Brouwer.

Il grado di Brouwer è un opportuno conteggio algebrico del numero degli zeri, in un insieme aperto limitato, di una mappa continua di uno spazio vettoriale n-dimensionale in se stesso, un conteggio che è invariante per perturbazioni sufficientemente piccole della mappa. Una delle conseguenze più semplici del grado di Brouwer è la versione n-dimensionale di Poincaré-Miranda del teorema di Bolzano per un cubo, e del teorema di punto fisso di Brouwer per una mappa continua di una bolla chiusa in se stessa.

Un altro approccio, che è fondamentale nel caso di un'equazione alle derivate parziali di tipo ellittico, per cui viene meno il metodo di shooting, consiste nel ridurre il problema di Dirichlet, o il problema periodico, a un'equazione integrale non lineare, cioè nel trovare un punto fisso di un operatore non lineare in un'opportuno spazio di Banach. Il grado di Brouwer dev'essere rimpiazzato dalla sua estensione a spazi di Banach, introdotta da Leray e Schauder. L'essenza del metodo di Leray-Schauder consiste nel deformare con continuità il problema in uno più semplice (spesso lineare), in modo tale che, durante la deformazione, l'insieme delle possibili soluzioni rimanga a priori limitato. Questo assicura che il grado di Leray-Schauder rimane constante durante la deformazione, e l'equazione originaria ha una soluzione se quella deformata più semplice ha un grado di Leray-Schauder non nullo. Diverse tecniche, come principi di massimo, disuguaglianze differenziali o integrali, metodi di blowing up, sono usati per ottenere i limiti a priori richiesti.

Una semplice conseguenza del grado di Leray-Schauder è il teorema di punto fisso di Schauder per mappe completamente continue di una bolla chiusa di uno spazio di Banach in se stessa. Questo teorema di punto fisso fornisce un'elegante dimostrazione per il metodo delle sotto- e soprasoluzioni, che implica l'esistenza di una soluzione del problema di Dirichlet, o del problema periodico, quando l'operatore differenziale non lineare associato mantiene opportuni segni costanti e opposti per due funzioni ordinate. Se ne danno applicazioni al problema di Neumann per equazioni non lineari ellittiche (soluzioni le cui derivata normale si annulla sul bordo del dominio) e alle soluzioni periodiche dell'equazione del pendolo forzato. Oltre all'esistenza, una questione importante è la molteplicità delle soluzioni.

Le tecniche del grado topologico portano a risultati importanti, specialmente nei problemi di biforcazione in cui si considera una famiglia di equazioni differenziali non lineari, ordinarie o alle derivate parziali, dipendenti da un parametro reale e aventi una soluzione (banale) nulla per tutti i valori del parametro. Il problema consiste nel trovare i valori del parametro in cui le soluzioni non nulle si biforcano da quella banale. Questa è una versione non lineare del problema spettrale per equazioni lineari. Infine, la ricerca di soluzioni positive di equazioni differenziali non lineari è importante anche nelle applicazioni alla fisica o alla biologia. La loro esistenza segue dall'assumere un diverso comportamento della non linearità all'orgine e all'infinito.

Uno strumento veramente efficace per provare questi risultati è il raffinamento del grado topologico, cioè l'indice di punto fisso per mappe da spazi infinito-dimensionali non lineari in sé.

Metodo di shooting

Equazioni differenziali scalari

A un livello molto elementare i metodi topologici intervengono nelle equazioni differenziali ordinarie quando un procedimento di cosiddetto shooting, introdotto nel 1905 da Carlo Severini, viene usato per risolvere il problema al contorno unidimensionale

[1] u″ = f(x,u,u′)

[2] u(0) = 0 = u(T)

dove f: [0,T]×ℝ×ℝ→ℝ e gli apici indicano l'operazione di derivata rispetto a x. Assumiamo, cosa che richiede smoothness e condizioni qualitative e di crescita per f, che esista nell'intervallo [0,T] un'unica soluzione u(t,c) di [1] con condizioni iniziali

[3] u(0) = 0 u′(0) = c.

Allora u(t,c) risolve [1]-[2] se e solo se c è soluzione dell'equazione scalare

[4] u(T;c) = 0.

Qualche informazione a priori sul comportamento di u(T;c) rispetto a c e il teorema di esistenza degli zeri di Bolzano sono usati per mostrare l'esistenza di una soluzione di [4]. Per esempio, se ∣f(x,u,v)∣≤M per ogni (x,u,v)∈[0,T]×ℝ×ℝ e per qualche M>0, allora Tc−(MT²/2)≤u(T;c)≤Tc+(MT²/2) per ogni c∈ℝ; questo implica che u(T;−R)≤0≤u(T;R) per tutti gli R>0 sufficientemente grandi e dunque che u(T;c)=0 per qualche c∈[−R,R].

Nel caso dell'equazione del pendolo forzato il problema di Dirichlet

[5] u″ + asinu = h(x), u(0) = 0 = u(T)

ha almeno una soluzione per ogni a∈ℝ e h continua sull'intervallo [0,T].

Sistemi di equazioni e teorema di Poincaré-Miranda

Per un sistema di equazioni differenziali, vale a dire quando u: [0,T]→ℝⁿ (n≥2) e

[6] f: [0,T]×ℝⁿ×ℝⁿ → ℝⁿ

nella [1], la [4] diventa un sistema di n equazioni nelle n componenti di c∈ℝⁿ.

Henri Poincaré, incontrando tale situazione nel 1883 in un problema di meccanica celeste, affermò e dimostrò la seguente versione n-dimensionale del teorema di Bolzano, successivamente chiamato teorema di Poincaré-Miranda per ragioni che saranno spiegate nel seguito:

Se P=[a₁,b₁]×…×[a_n,b_n], g: P→ℝⁿ è continua e, per ogni 1≤j≤n, le g_j hanno segno opposto nelle j-esime facce opposte [a₁,b₁]×…×{a_j}×…×[a_n,b_n] e [a₁,b₁] × …×{b_j}× …×[a_n,b_n] di P, allora g ha almeno uno zero c in P.

Dunque, per il problema [1]-[2] con f data da [6] sufficientemente liscia e tale che ∣∣f(x,u,v)∣∣≤M per ogni

[7] formula

implicano che le condizioni del teorema di Poincaré-Miranda sono soddisfatte per g(c)≡u(T;c), P=[−R,R]ⁿ e R>0 sufficientemente grande.

L'operatore di Poincaré e il teorema di punto fisso di Brouwer

La riduzione a un sistema di equazioni interviene già per l'equazione scalare [1] quando, al posto della [2], si considerano le condizioni al contorno periodiche

[8] u(0) = u(T) u′(0) = u′(T).

La soluzione u(t;c₁,c₂) del problema di Cauchy

[9] u(0) = c₁ u′(0) = c₂

per l'equazione [1], supponendo che esista e sia unica su [0,T], risolve il problema con valori al contorno periodici [1]-[8] se e solo se (c₁,c₂) è una soluzione del sistema

[10] c₁ = u(T;c₁,c₂), c₂ = u′(T;c₁,c₂).

In altre parole, (c₁,c₂) deve essere un punto fisso per l'operatore di Poincaré P_T

[11] P_T(c₁,c₂) (u(T;c₁,c₂), u′(T;c₁,c₂)).

Il teorema del valor intermedio n-dimensionale di Poincaré fu rapidamente dimenticato e nel 1941, ignaro del contributo del grande matematico francese, Carlo Miranda provò la sua equivalenza con un famoso teorema topologico di punto fisso provato nel 1912 da Luitzen E. J. Brouwer: ogni mappa continua h: P→P ha almeno un punto fisso.

Come è facilmente osservabile, P può essere sostituito da un qualsiasi insieme C omeomorfo a P, e in particolare da una bolla chiusa in ℝⁿ. Questo teorema di punto fisso fu un sottoprodotto della vasta teoria topologica di Brouwer sul grado di una mappa continua, introdotto inizialmente per risolvere il problema dell'invarianza della dimensione. La dimostrazione suggerita da Poincaré del teorema di Poincaré-Miranda era basata su un precursore analitico del grado di Brouwer, introdotto per mappe lisce da Leopold Kronecker nel 1869.

Grado di Brouwer

Calcolo algebrico delle soluzioni

Anche se originariamente Brouwer definì il suo grado per mappe continue tra due varietà orientate della stessa dimensione finita, in analisi è più conveniente introdurlo per mappe continue g: D_⊂ℝⁿ→ℝⁿ tali che

[12] 0 ∉ g(∂D)

dove D è aperto e limitato e indica la sua chiusura in ℝⁿ. Se g è liscia e detg′(c)≠0 per ogni c∈D tale che g(c)=0, la controimmagine g⁻¹(0) di 0 contiene un numero finito di punti e il grado di g stessa su D è definito da

[13] formula

ovvero dalla somma algebrica del numero dei suoi zeri: a questi è assegnato il valore +1 se il corrispondente determinante dello Jacobiano g′(c) è positivo e −1 se è negativo. In particolare, se I indica l'applicazione identica di ℝⁿ in ℝⁿ considerata come mappa da D_ in ℝⁿ, abbiamo allora d_B[I,D]=1 se 0∈D o d_B[I,D]=0 se 0∉D_.

In contrasto con il conteggio banale (ottenuto assegnando il valore +1 a tutti gli zeri), quello algebrico risulta essere insensibile a piccole perturbazioni di g (rispetto alla norma uniforme) e un opportuno procedimento di limite fornisce il grado di Brouwer d_B[g,D] su D per ogni mappa continua g: D_→ℝⁿ che verifica la [12]. Per costruzione, si ha la proprietà di esistenza: se d_B[g,D]≠0 allora g ha almeno uno zero in D.

Il fatto che il grado sia insensibile a piccole perturbazioni di g implica la sua invarianza per omotopia. Più precisamente, se G: [0,1]×D_→ℝⁿ è continua e tale che 0∉G([0,1]×∂D) allora d_B[G(t,∙),D] è costante per ogni t∈[0,1]. Segue che d_B[g,D] dipende esclusivamente dal valore di g su ∂D. Se Bⁿ è la bolla unitaria in ℝⁿ e Sⁿ⁻¹ il suo contorno, si può definire il grado di Brouwer degφ per ogni funzione continua φ: Sⁿ⁻¹→Sⁿ⁻¹ come d_B[Φ,intBⁿ], dove Φ è una qualunque estensione di φ a Bⁿ.

Mappe armoniche

Il problema di Dirichlet, fondamentale nello studio di numerosi problemi della fisica classica e moderna, consiste nel trovare una funzione reale u armonica in qualche dominio limitato Ω⊂ℝⁿ, ossia

[14] formula

in Ω, e uguale sul contorno ∂Ω a una assegnata funzione continua φ: ∂Ω→ℝⁿ.

A una tale funzione corrisponde un minimo dell'integrale dell'energia

[15] formula

valutato su tutte le funzioni lisce uguali a φ su ∂Ω. Sotto ragionevoli ipotesi di regolarità per Ω, la soluzione u per il problema di Dirichlet esiste, è unica ed è liscia in Ω.

Diverse questioni di geometria e fisica portano a generalizzare questo problema al caso di funzioni u: M→N, dove M e N sono varietà di dimensione finita. Queste u vengono chiamate mappe armoniche. Per esempio, lo studio dei cristalli liquidi porta al caso M=B³, N=S², mentre quello dei superfluidi e dei semiconduttori a M=B²,B³ e N=S¹.

A differenza delle funzioni armoniche, le mappe armoniche possono (e a volte devono) presentare delle singolarità ‒ fisicamente importanti perché corrispondono per esempio ai difetti nei cristalli o ai vortici nei fluidi ‒ le cui origini possono essere topologiche.

Haïm Brézis, Jean-Michel Coron e Elliot H. Lieb mostrarono nel 1986 che la mappa armonica u: B³→S², uguale all'identità su ∂B³ e tale da minimizzare l'integrale dell'energia ∫_B3∣∣∇u∣∣², è data da u(x)=x/∣∣x∣∣. Più in generale, ogni mappa armonica u: B³→S², uguale sul contorno ∂B³ a una funzione φ con degφ≠0, è discontinua in qualche punto interno a B³: infatti una mappa continua u: B³→S² si annullerebbe in B³, una contraddizione.

Il grado di Brouwer è inoltre utile per analizzare la natura delle singolarità e tali questioni portarono nel 1995 Brezis e Louis Nirenberg a estendere questo concetto ad alcune classi di mappe non continue.

Approccio di punto fisso per problemi al contorno unidimensionali

Equazione integrale equivalente

Il metodo di shooting mostra che per ogni funzione continua h: [0,T]→ℝⁿ il problema di Dirichlet lineare

[16] u″ = h(x) per x∈(0,T) u(0) = 0 = u(T)

ha l'unica soluzione

[17] formula

dove la funzione di Green G(x,s) è facilmente definita.

Di conseguenza, risolvere il problema [1]-[2] equivale a trovare u di classe C¹ (e cioè con derivata prima continua) su [0,T] che soddisfa l'equazione integrale non lineare

[18] formula.

Se consideriamo lo spazio di Banach C^k delle funzioni u: [0,T]→ℝⁿ di classe C^k (k≥0), dotato della classica norma

[19] formula

e se f: [0,T]×ℝⁿ×ℝⁿ→ℝⁿ è continua, l'applicazione u→Φ(u) definita dal termine a secondo membro della [18] mappa in modo continuo C¹ in C¹. Inoltre, dal teorema di Ascoli-Arzelà segue che Φ mappa insiemi limitati di C¹ in insiemi relativamente compatti di C¹. Un'applicazione Φ con tali proprietà è detta completamente continua in C¹.

Teorema di punto fisso di Schauder

Generalizzando alcuni lavori pionieristici di George D. Birkhoff e Oliver Kellogg (1922) per particolari spazi di funzioni, Juliusz Schauder estese nel 1930 il teorema di punto fisso di Brouwer alle mappe completamente continue di insiemi C convessi, chiusi e limitati di uno spazio di Banach X in se stessi (teorema di punto fisso di Schauder). Più precisamente se C è un insieme convesso, chiuso e limitato di uno spazio di Banach X, ogni mappa continua Φ:

compatto ha almeno un punto fisso.

Quando ∣∣f(t,u,v)∣∣≤M per ogni (t,u,v)∈[0,T]×ℝⁿ×ℝⁿ, ∣∣Φ(u)∣∣₁≤R per ogni u∈C¹ e per un qualche R>0. Segue che Φ: B_(R)→(R), con B(R) la bolla aperta di C¹ con centro nell'origine (in questo caso la funzione nulla) e raggio R. Per il teorema di punto fisso di Schauder, Φ ha almeno un punto fisso, e il problema [1]-[2] almeno una soluzione. Rispetto al metodo di shooting, questo approccio analitico-funzionale richiede proprietà di regolarità meno stringenti per f e nessuna conoscenza del problema di Cauchy per il sistema corrispondente.

Il problema di Dirichlet per equazioni ellittiche semilineari

Approccio di punto fisso

Una generalizzazione naturale del problema [1]-[2] per le equazioni differenziali alle derivate parziali è il problema di Dirichlet, costituito dall'equazione ellittica semilineare

[20] Δu = f(x,u,∇u) per x∈Ω

che soddisfi sul contorno la condizione di Dirichlet

[21] u = 0 per x∈∂Ω

dove Ω⊂ℝⁿ è un dominio aperto limitato e f: Ω_×ℝ×ℝⁿ→ℝ è sufficientemente liscia.

Siccome il problema di Cauchy non è ben posto per una equazione ellittica (anche nel caso lineare), non esiste speranza di estendere il metodo di shooting a questa situazione. Ma, assumendo se necessario qualche proprietà di regolarità su ∂Ω‚ il problema di Dirichlet lineare

[22] Δu = h(x) per x∈Ω u = 0 per x∈∂Ω

ha un'unica soluzione (eventualmente generalizzata) per tutte le h appartenenti a opportuni spazi di funzioni che rendano possibile un approccio di punto fisso.

Soluzioni classiche e forti

Se α∈]0,1[, k≥0 e C^k,α(Ω_) denota lo spazio hölderiano delle funzioni reali di classe C^k su Ω_ tali che la norma

[23] formula

è finita, il problema [22] ha un'unica soluzione classica u∈C^2,α(Ω_) per ogni h∈C^0,α(Ω_).

Similmente, se p>1 e W^k,p(Ω) denota lo spazio di Sobolev delle funzioni reali u con derivate deboli fino all'ordine k appartenenti a L^p(Ω) e norma

[24] formula.

e W₀^k,p(Ω) indica la chiusura in W^k,p(Ω_) del sottospazio delle funzioni lisce a supporto compatto in Ω, allora per ogni h∈L^p(Ω) il problema [22] ha un'unica soluzione (forte) u∈W₀^2,p(Ω).

L'inclusione compatta di C^2,α(Ω_) in C^1,α(Ω_) e di W₀^2,p(Ω) in W₀^1,p(Ω) implica che gli operatori lineari K₁: C^0,α(Ω_)→C^1,α(Ω_) e K₂: L^p(Ω)→W^1,p(Ω) che associano a ogni h l'unica soluzione u di [22] sono compatti.

Non linearità limitate

Se f: Ω_×ℝ×ℝⁿ→ℝ soddisfa alcune condizione di regolarità (dipendenti dal tipo di soluzione considerata), e N_f: u→f(∙,u(∙),∇u(∙)) è l'operatore di Nemitsky associato, il problema di Dirichlet [20]-[21] è equivalente al problema di punto fisso

[25] u = K₁N_f (u) (rispettivamente u=K₂N_f (u))

nello spazio C^1,α(Ω_) (rispettivamente W^1,p(Ω)). Il teorema di punto fisso di Schauder implica che per ogni funzione continua e limitata f: Ω×ℝ×ℝⁿ→ℝ il problema [20]-[21] ha almeno una soluzione debole u∈W₀^1,p(Ω).

La condizione di limitatezza di f è molto restrittiva, e sono stati fatti molti sforzi indebolirla.

Sotto- e soprasoluzioni ordinate

Sotto- e soprasoluzioni

Un modo per provare l'esistenza di soluzioni per i problemi ellittici semilineari del secondo ordine con varie condizioni al contorno e non linearità non limitate è il metodo delle sotto- o soprasoluzioni, introdotto da Giuseppe Scorza Dragoni nel 1931 per le equazioni differenziali ordinarie e da Jin-Ichi Nagumo nel 1954 per le equazioni ellittiche semilineari. L'approccio qui sotto delineato funziona essenzialmente in entrambi i casi, ed è descritto per semplicità nel caso del problema periodico

[26] u″ = f(x,u) u(0) = u(T), u′(0) = u′(T).

Le funzioni α,β∈C² sono dette sotto- (rispettivamente, sopra-) soluzione del problema [26] se

[27] α″(x) ≥ f(x,α(x)) per x∈]0,T[

        α(0) = α(T) α′(0) ≥ α′(T)

          β″(x) ≤ f(x,β(x)) per x∈]0,T[

              β(0) = β(T) β′(0) ≤ β′(T)

Un fondamentale risultato di esistenza

L'esistenza di una soluzione segue da quella di una coppia ordinata di sotto- e soprasoluzioni: se il problema [26] ha una sottosoluzione α e una soprasoluzione β, le quali verificano α″(x)≤β″(x) per ogni x∈[0,T], allora esso ha almeno una soluzione u che verifica α(x)≤u(x)≤β(x) per ogni x∈[0,T].

Per provare questo risultato, per prima cosa si costruisce un problema modificato che sia più trattabile:

[28] u″−u = f(x,γ(x,u))−γ(x,u)

  u(0) = u(T)                u′(0) = u′(T)

dove rispettivamente γ(x,u)=α(x), γ(x,u)=u o γ(x,u)=β(x) se u〈α(x), α(x)≤u(x)≤β(x) oppure u>β(x): in questo caso [26] e [28] coincidono quando α(x)≤u(x)≤β(x). Ora, come nel paragrafo 3, il problema lineare

[29] u″−u = h(x) u(0) = u(T) u′(0) = u′(T)

ha per ogni h∈C⁰ un'unica soluzione u(x)=∫₀^TG∼(x,s)h(s)ds, con G∼ una funzione di Green appropriata. Poiché il termine a secondo membro del problema [28] è limitato, il teorema di punto fisso di Schauder implica che esso ha almeno una soluzione u∼. Una dimostrazione per assurdo, basata sulle usuali caratterizzazioni di massimo e minimo, prova che α(x)≤u∼(x)≤β(x) per ogni x∈[0,T], cosicché u∼ è una soluzione di [26].

Non linearità non decrescenti

Quando f e ∂Ω sono sufficientemente regolari, il metodo delle sotto- e soprasoluzioni può essere utilizzato per il problema ellittico semilineare

[30] Δu = f(x,u)

in un dominio aperto limitato Ω⊂ℝⁿ, con condizioni di Dirichlet [21] o condizioni di Neumann (ν(x) denota la normale esterna a ∂Ω nel punto x)

[31] formula.

Una semplice conseguenza è un'elegante condizione necessaria e sufficiente di esistenza dovuta a Jerry L. Kazdan e Frank W. Warner (1975): se f(x,c) è non decrescente in c per ogni x fissata, il problema di Neumann [30]-[31] ha almeno una soluzione classica se e solo se

[32] formula

per qualche c∈ℝ.

Infatti, se [31]-[32] ha una soluzione classica u con u_m≡min_Ω_u, u_M≡max_Ω_u, integrando entrambi i membri di [30] su Ω e usando il teorema della divergenza e la monotonia di f(x,∙) si ha

[33] formula

da cui segue la necessità. Per la sufficienza, se la condizione [32] è soddisfatta e U(x) è l'unica soluzione classica del problema di Neumann lineare

[34] formula,

allora

[35] formula

sono soluzioni ordinate inferiori e superiori per [30]-[31], da cui segue il risultato.

Equazione del pendolo forzato periodicamente

Sotto- e soprasoluzioni costanti

Le sotto- e soprasoluzioni costanti forniscono un'utile condizione di esistenza:

se esistono costanti α≤β tali che f(x,a)≤0≤f(x,b) per ogni x∈[0,T], il problema [26] ha almeno una soluzione u con α≤u(x)≤β per ogni x∈[0,T].

Per esempio, prendendo β=R=−α per R>0 sufficientemente grande, il problema

[36] u″ = p(u) + h(x) u(0) = u(T) u′(0) = u′(T)

ha almeno una soluzione per ogni h continua, quando p è un polinomio reale di ordine dispari il cui termine di ordine massimo ha un coefficiente positivo.

Pendolo forzato: un confronto tra equazione esatta e equazione approssimata

Le considerazioni precedenti possono essere applicate all'equazione di Duffing con a>0

[37] formula.

È questa la prima approssimazione non lineare dell'equazione del pendolo forzato, introdotta nel 1918 da Georg W. Duffing. Tuttavia, per l'equazione esatta del pendolo:

condizione necessaria per l'esistenza di una soluzione del problema

[38] u″ = asenu = h(t) u(0) = u(T), u′(0) = u′(T)

(con a>0) è

[39] formula

come segue integrando entrambi i membri sull'intervallo [0,T].

Decomposizione di Lyapunov-Schmidt

Per trovare una condizione necessaria e sufficiente per [38], grazie a Dancer (1976), si decompone y∈C⁰ come y(x)=y_ +y∼(x) con

[40] formula

in modo tale che y∼∈C∼:={y∈C⁰: y_=0}. La decomposizione di Lyapunov-Schmidt fu introdotta indipendentemente da Lyapunov nel 1906 e da Schmidt nel 1908:

u=ū+ũ è una soluzione di [38] se e solo se (ū,ũ) è una soluzione di

[41] formula

[42] formula.

Nel metodo classico di Liapunov-Schmidt, l'equazione ausiliaria [41] è risolta prima in ũ per ogni ū fissata (usando il teorema di punto fisso o il teorema delle funzioni implicite, o la teoria del punto critico) e la soluzione viene sostituita nella [42] per fornire un'equazione di biforcazione.

Dato ẽ∈C∼, se Hẽ denota l'unica soluzione del problema elementare

[43] u″ = ẽ, u(0) = u(T), u′(0) = u′(T), ū = 0

[41] è equivalente al problema di punto fisso in C∼

[44] formula

con Φ(ū,ũ) limitata e completamente continua in C∼ per ogni ū fissata, e 2π-periodica in ū per ogni ũ fissata. Dal teorema di punto fisso di Schauder, [41] ha almeno una soluzione ũ per ogni ū fissata.

Se S_h∼⊂ℝ×C∼ denota l'insieme delle coppie (ū,ũ) tali che ū∈ℝ e ũ è soluzione di [41], la proiezione di S_h∼ su ℝ è ℝ e [38] ha una soluzione se e solo se h_ appartiene all'insieme

[45] formula.

I_h⁻≠0 è un intervallo poiché se h−₁〈h−₂ appartengono a I_h⁻, e h∈] h−₁,h−₂[, le soluzioni u₁, u₂ di [38] con h=h₁+h, h=h₂+h, sono rispettivamente una sotto- e soprasoluzione di [38], cosicché α=u₂ e β=u₁+2kπ sono sotto- e soprasuluzioni ordinate di [39] per k∈ℕ sufficientemente grande. Il teorema di Ascoli-Arzelá implica che I_h⁻ è chiuso, si ha dunque: per ogni h∼∈C∼, il problema [38] con h=h_+h∼ ha una soluzione se e solo se h_∈I_h∼.

È facile vedere che I₀=[−a,a], ma ancora non è noto se, per qualche h∼, I_h∼ può essere ridotto ad un punto (problema di degenerazione). Mawhin e Willem provarono nel 1984 che l'insieme delle h∼ per cui I_h∼ ha interno non vuoto, è aperto e denso in C∼, che esistono almeno due soluzioni (che non differiscono di un multiplo di 2π) se h∼ è interno a I_h∼ e, usando la teoria del punto critico, che 0∈I_h∼ per ogni h∼∈C∼.

Metodo di continuazione di Leray-Schauder

Il grado di Leray-Schauder

In un fecondo lavoro del 1934, Leray e Schauder estesero il grado di Brouwer alle mappe della forma f=I−Φ con Φ : Ω_→X compatta (continua e Φ (Ω_) compatto), 0∉f(∂Ω) e Ω⊂X aperto e limitato. L'idea consiste nell'approssimare Φ in Ω con mappe Φ_n a valori in sottospazi finito-dimensionali X_n di X e nel mostrare che i gradi di Brouwer d_B[(I−Φ_n)∣X_n,Ω∩X_n], si stabilizzano per n molto grande. Il loro valore limite d_LS[f,Ω], chiamato grado di Leray-Schauder di f rispetto a Ω, mantiene le proprietà essenziali del grado di Brouwer.

In merito ai teoremi di esistenza, una conseguenza veramente utile della teoria del grado è il teorema di continuazione di Leray-Schauder:

assumiamo che J⊂ℝ sia un intervallo chiuso e Ψ: X×J→X completamente continua. Se esiste qualche R>0 tale che l'insieme S delle coppie (u,λ) tali che u=Ψ(u,λ) è contenuto in B_R×J, e se d_LS[I−Ψ(∙,λ₀),B_R]≠0 (in particolare se Ψ(∙,λ₀)=0 ) per qualche λ₀∈J, allora S contiene un continuo C la cui proiezione su J è J.

La sua dimostrazione combina l'invarianza omotopica e le proprietà di esistenza del grado attraverso argomenti di connessione. Il nome 'continuazione' esprime il fatto che il punto fisso per λ=λ₀ continua ad esistere per tutti i λ∈J.

Certamente, la parte difficile in questo teorema è trovare, dalle equazioni u=Ψ(u,λ) il limite a priori R per u. Molte tecniche di analisi elevata, come i principi del massimo, le disuguaglianze integrali, i metodi di blowing up sono utili in questo contesto.

Equazione di Duffing

Stime a priori basate sui principi del massimo sono già state usate nel trattare le sotto- e soprasoluzioni. Come semplice esempio dell'utilizzo delle disuguaglianze integrali, consideriamo l'equazione di Duffing con a>0, b>0, c>0,

[46] u″+cu′+au+bu³=h(x), u(0)=u(T), u′(0)=u′(T)

e introduciamo l'omotopia (con λ∈[0,1])

[47] u″+cu′+au+λbu³=λh(x), u(0)=u(T), u′(0)=u′(T).

La [47] può essere scritta come un problema di punto fisso

[48] formula

per una qualche funzione di Green ‸G che dipende solo da c, a e T. Per λ=0, l'unica soluzione è u=0. Se λ∈]0,1] e u è una possibile soluzione di [47], moltiplicando entrambi i membri dell'equazione [47] per u′, integrando su [0,T], e usando le condizioni al contorno e la disuguaglianza di Cauchy-Schwarz otteniamo la stima a priori

[49] formula.

Moltiplicando entrambi i membri dell'equazione [47] per u, integrando su [0,T], e usando la [49] abbiamo

[50] formula,

che, insieme a [49], dà R=R(b,c,T) tale che ∣∣u∣∣〈R. L'esistenza di una soluzione per [46] segue dal teorema di continuazione di Leray-Schauder.

Il caso c=0 è più delicato per la mancanza di limitazioni a priori per l'insieme delle possibili soluzioni (anche quando h=0). L'esistenza di almeno una soluzione periodica può ancora essere ottenuta raffinando le tecniche di Leray-Schauder. L'esistenza di infinite soluzioni è stata dimostrata solo usando tecniche sofisticate del tipo di Morse nella teoria dei punti critici, la quale si applica anche ai sistemi superlineari di Duffing della forma

[51] u″ + ∇G(u)= e(x), u(0) = u(T), u′(0) = u′(T)

e ai problemi di Dirichlet superlineari

[52] Δu + ∇G(u)= e(x) in Ω, u = 0 su ∂Ω

dove G è superquadratica e soddisfa delle condizioni di crescita appropriate.

Sotto- e soprasoluzioni non ordinate

L'esempio

[53] u″ + u= senx, u(0) − u(2π) = 0 = u′(0) = u′(2π)

che non ha una soluzione (risonanza) ed ha sotto- e soprasoluzione (non ordinata) α=1 β=−1 mostra come il metodo della sotto- e soprasoluzione fallisce in generale nel caso non ordinato.

Herbert Amann, Antonio Ambrosetti e Giovanni Mancini mostrarono nel 1978 che una combinazione del teorema di continuazione di Leray-Schauder, con la decomposizione di Lyapunov-Schmidt e il classico metodo delle sotto- e soprasoluzione porta all'esistenza, in questa situazione, sotto ulteriori condizioni. Ancora, si prende per esempio il problema [26], si assume che f sia limitata su [0,T]×ℝ, e si procede come nel caso dell'equazione del pendolo forzato. Il teorema di Leray-Schauder applicato all'equazione ausiliaria di Lyapunov-Schmidt

[54] formula

considerata come un'equazione in C∼ con parametro ũ∈ℝ, dà un continuo C di soluzioni (ũ,ū) di [54] la cui proiezione su ℝ è ℝ. Siano α e β rispettivamente una sotto- e soprasoluzione di [26].

Se

per qualche (ũ,ū)∈C, [26] ha una soluzione. Se

per ogni (ũ,ū)∈C, ū+ũ è una soprasoluzione per ogni (ũ,ū)∈C, più grande di α per ū sufficientemente grande. Dunque [26] ha una soluzione. Similmente se

per ogni (ũ,ū)∈C, dunque si ha:

Se f è limitata e [27] ha una sotto- e soprasoluzione, allora ha una soluzione.

La condizione di limitatezza può essere sostituita da appropriate condizioni di crescita lineari.

Soluzioni multiple e di biforcazione

Biforcazione di soluzioni e autovalori

Una barra elastica compressa lungo la direzione del suo asse si curva se la pressione è sufficientemente grande. Il problema fu già considerato da Eulero nel 1744. Se u denota l'angolo tra l'asse e la tangente del bastone, λ la pressione e T la lunghezza del bastone, l'equazione, con condizioni agli estremi fissate, può essere scritta

[55] u″ + λsenu = 0, u(0) = 0 = u(T).

Ovviamente u≡0 è sempre una soluzione (nessun incurvamento), e chiamata 'soluzione banale'.

(λ*,0) è chiamato punto di biforcazione per [55] se, per ogni r>0, [λ*−r,λ*+r]×B(R) contiene una soluzione (λ,u) di [55] con u≠0, dove B(R)⊂C⁰. Un facile argomento di funzioni implicite implica che:

se (λ*,0) è un punto di biforcazione per [55], allora λ* è un autovalore di

[56] u″ + λu = 0, u(0) = 0 = u(T)

ossia

[57] formula

Biforcazione e grado

Il problema [55] può essere scritto come problema di punto fisso in C⁰

[58] formula.

M.A. Krasnosel'skii per primo mostrò nel 1950 come usare il grado per individuare i punti di biforcazione delle mappe completamente continue Φ:X→X tali che Φ(0)=0.

La definizione di punto di biforcazione per u=λΦ(u) è lo stesso del caso speciale di una barra elastica. Se (λ*,0) non è un punto di biforcazione, si possono trovare λ₋〈λ*〈λ₊ e r>0 tali che λΦ abbia solamente il punto fisso 0 in B(r)__. Dall'invarianza di omotopia d_LS[I−λΦ,B(r)] è costante su [λ₋,λ₊]; conseguentemente:

se λ₋〈λ₊ sono tali che d_LS[I−λ₋Φ,B(r)]≠d_LS[I−λ₊Φ,B(r)], allora [55] ha un punto di biforcazione (λ*,0) per qualche λ*∈[λ₋,λ₊].

Ora, una formula di Leray-Schauder (1934) mostra che per una mappa completamente continua Φ: X→X di classe C¹ con differenziale di Fréchet Φ′(0) in 0

Se λ₋⁻¹ λ₊⁻¹ non sono autovalori di Φ′(0), allora, per r>0 piccolo,

[59] d_LS[I−λ₊Φ,B(r)] = (−1)^σd_LS[I−λ₋Φ,B(r)]

dove σ è la somma della molteplicità degli autovalori di Φ′(0) i cui reciproci sono posti tra λ₋ e λ₊.

Poiché tutti gli autovalori di [56] sono semplici, si ha, per la barra elastica, se ]λ₋,λ₊[ contiene solamente l'autovalore n²π²/T²,

[60] d_LS[I− λ₋Φ,B(r)] = −d_LS[I− λ₊Φ,B(r)]

cosicché:

per ogni n=1,2,…,(n²π²/T²,0) è un punto di biforcazione per [55].

Per il problema generale u=λΦ(u), si applica lo stesso argomento ad ogni autovalore di Φ′(0) con molteplicità dispari.

Struttura globale dei rami di biforcazione

Combinando l'invarianza per omotopia del grado di Leray-Schauder con qualche argomento di connessione, Rabinowitz ottenne nel 1971 un'informazione globale sui rami di biforcazione:

Se λ_n⁻¹ è un autovalore di Φ′(0) con molteplicità dispari e S_n è la componente dell'insieme

[61] formula

contenente (λ_n⁻¹,0), allora S_n è non limitato oppure contiene un numero finito di punti (λ_m⁻¹,0)(m≠n) .

Usando le proprietà delle autofunzioni e i teoremi di confronto per le equazioni lineari del secondo ordine, si può mostrare, nel caso [55], che ogni componente S_n è non limitata e contenuta in

[62] formula

In particolare, poiché −u è soluzione insieme con u:

[55] ha, per ogni

[63] formula

almeno n coppie distinte di soluzioni.

Soluzioni positive

Indice di punto fisso

In molte applicazioni, è importante trovare 'soluzioni positive'. L'approccio topologico a tali problemi porta ad estendere il grado di Leray-Schauder alle mappe definite su coni chiusi o cunei, o, più in generale, sugli insiemi chiusi convessi C, invece che spazi di Banach, in modo da considerare solo, per i loro insiemi aperti, il relativo contorno ∂C.

Sia C⊂X un insieme chiuso convesso. Per il teorema di Dugundji (1951), esiste una contrazione ϱ: X→C (continua su X e uguale all'identità su C). Sia Ω⊂C limitato e relativamente aperto in C, e f=I−Φ, con Φ: Ω__→C compatta e 0∉f(∂CΩ). Allora, se B(R)⊃Ω__, il grado di Leray-Schauder d_LS[I−Φ∘ϱ,B(r)∩ϱ⁻¹(Ω)] è ben definito, indipendente da R e ϱ, ed è chiamato indice di punto fisso di Φ in C rispetto a Ω, e denotato con i_C[Φ,Ω]. Un caso particolare importante è il cono chiuso positivo in uno spazio ordinato di Banach.

Soluzioni positive delle equazioni ellittiche semilineari

Un'applicazione di questa tecnica è lo studio delle soluzioni positive del problema di Dirichlet

[64] Δu + f(x,u) = 0 in Ω, u = 0 su ∂Ω

dove Ω⊂ℝⁿ è limitato, ∂Ω liscio, f è continua e positiva su Ω__×ℝ.

Sia λ₁ il più piccolo autovalore del problema di Dirichlet su Ω per −Δ, e φ₁ una corrispondente autofunzione positiva. Il seguente risultato è essenzialmente dovuto a De Figueiredo, P.L Lions e Nussbaum (1982):

Assumiamo che le condizioni seguenti valgano uniformemente in x∈Ω__, per qualche p∈]1,(N+2)/(N−2)[ per N≥3, p>1 per N=1,2, e qualche funzione positiva h:

[65] formula

[66] formula

Allora [65] ha almeno una soluzione positiva.

La condizione [64] ci permette di dimostrare per contraddizione l'esistenza di una costante C=C(p,Ω,f)>0 tale che ogni possibile soluzione non negativa di [64] soddisfa u(x)≤C per ogni x∈Ω. Se non è questo il caso, un metodo di blowing up prova l'esistenza di una soluzione positiva non banale dell'equazione Δu+u^p=0 sull'intero spazio o su un semispazio, anche se tale problema ha solamente la soluzione banale (teorema tipo-Liouville).

La condizione all'infinito in [66] implica che ogni possibile soluzione (u,t) (con t≥0) del problema

[67] Δu + f(x,u) + tφ₁(x) = 0 su Ω, u = 0 su ∂Ω

soddisfa

[68] formula

per qualche C>0. Infine, scrivendo il problema [64] come un problema di punto fisso u=Φ(u) da C(Ω__)∩P con P il suo cono positivo, la condizione all'infinito in [66] restituisce qualche R>0 per cui il problema [67] non ha soluzioni con ∣∣u∣∣=R, il che implica i_C[Φ,B(R)∩P]=0, e la condizione in zero nella [66] dà 0〈r〈R tale che i_C[Φ,B(R)∩P]=1. Allora i_C[Φ,(B(R)B_(R))∩P]=−1 e [64] ha una soluzione non banale.

Bibliografia

Bethuel 1994: Bethuel, Fabrice - Brézis, Haïm - Hélein, Frédéric, Ginzburg-Landau vortices, Boston, Birkhäuser, 1994.

Brown 2004: Brown, Robert F., A topological introduction to nonlinear analysis, 2. ed., Boston, Birkhäuser, 2004.

Chang 2005: Chang, Kung-Ching, Methods in nonlinear ana-lysis, Berlin, Springer, 2005.

De Coster, Habets 2006: De Coster, Colette - Habets, Patrick, Two point boundary value problems. Lower and upper solutions, Amsterdam, Elsevier, 2006.

Fitzpatrick 1993: Fitzpatrick, Patrick e altri, Topological methods for ordinary differential equations, Berlin, Springer, 1993.

Krasnosel'skii, Zabreiko 1984: Krasnosel'skii, Mark A. - Zabreiko, Petr P., Geometrical methods of nonlinear ana-lysis, Berlin, Springer, 1984.

Matzeu, Vignoli 1995-1997: Topological nonlinear analysis, edited by Michele Matzeu, Alfonso Vignoli, Boston, Birkhäuser, I-II, 1995-1997.

Mawhin 1979: Mawhin, Jean, Topological degree methods in nonlinear boundary value problems, Providence (R.I.), American Mathematical Society, 1979.

Zeidler 1986-1988: Zeidler, Eberhard, Nonlinear functional analysis and its applications, Berlin, Springer, I-IV, 1986-1988.