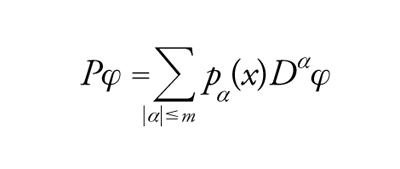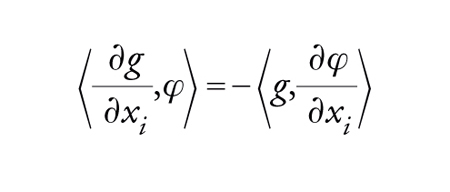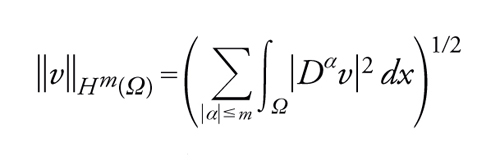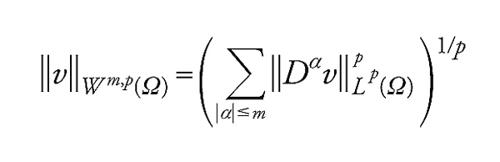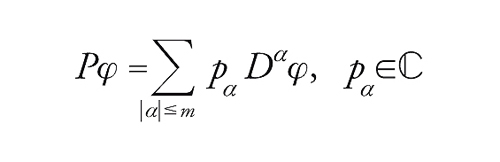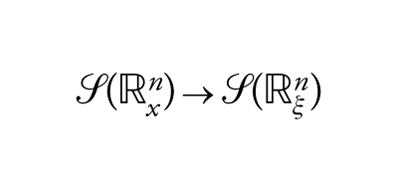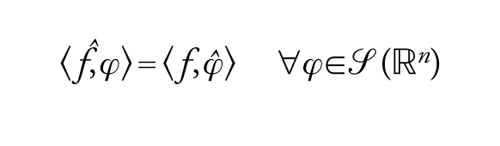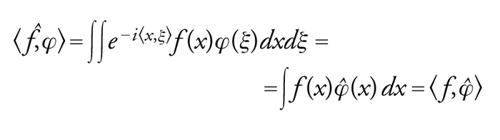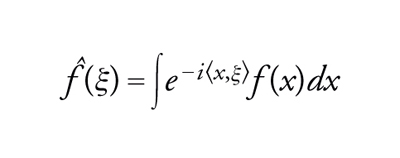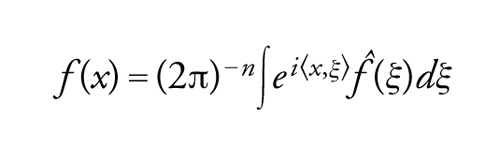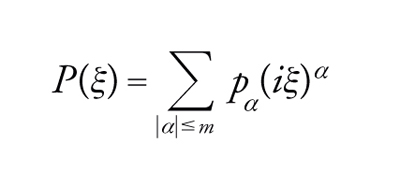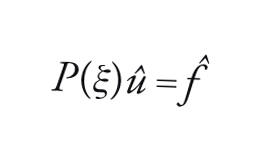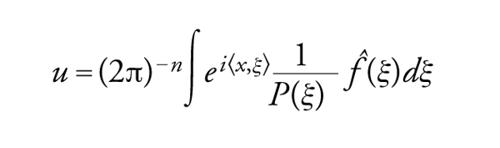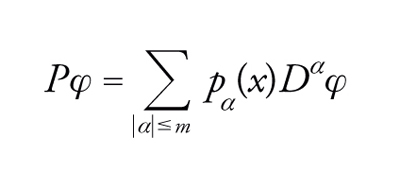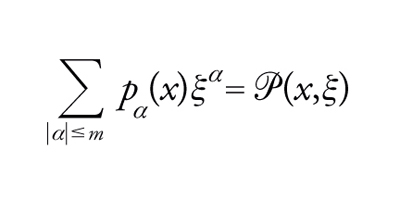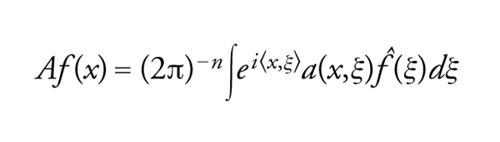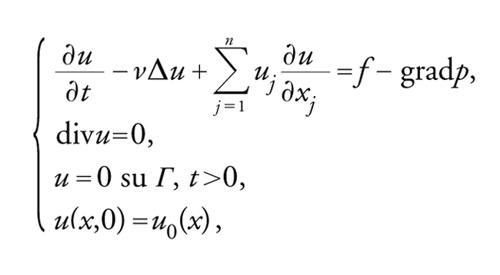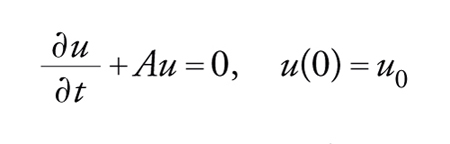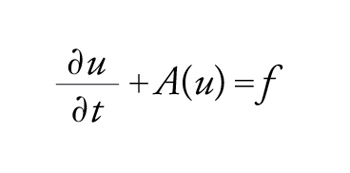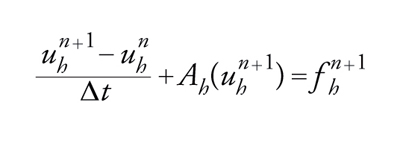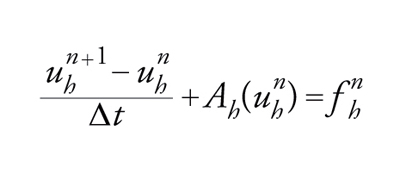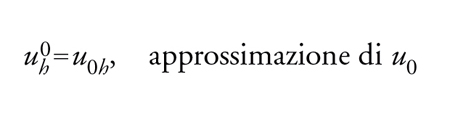Equazioni funzionali
Equazioni funzionali
La teoria delle equazioni funzionali si è sviluppata a stretto contatto con i problemi via via sorti nelle varie scienze, a partire dalla meccanica, e dalla fisica. Per prima si è sviluppata la teoria delle equazioni differenziali ordinarie, la quale d'altronde continua a porre problemi di estremo interesse come per esempio tutte le tematiche riguardanti la stabilità delle soluzioni. Parallelamente, varie questioni di fisica fra le quali i classici problemi scaturiti dalla teoria del calore e dalla teoria delle lamine vibranti, hanno fatto sorgere vari tipi di problemi con equazioni alle derivate parziali con opportune condizioni al contorno. È ugualmente importante studiare i problemi stazionari associati ai problemi precedenti: essi si ottengono sopprimendo le derivate rispetto al tempo nelle relative equazioni. Il problema tipo è quello di Dirichlet.
I precedenti problemi rientrano nella categoria dei problemi al contorno delle equazioni lineari. Ma la teoria lineare è essenzialmente insufficiente per un gran numero di fenomeni fisici, come quelli per esempio in cui spostamenti troppo grandi o velocità troppo elevate non giustificano più le ipotesi di linearizzazione, che si sono dimostrate indispensabili per ricavare le equazioni precedenti. Questo è il caso della maggior parte dei fenomeni dell'idrodinamica e di molti altri fenomeni che si incontrano nella teoria dell'elasticità, ove si abbiano grandi spostamenti, nella teoria della meccanica unilaterale, sulla quale torneremo in seguito, nella teoria della meccanica statistica, ecc.
Uno dei più noti modelli non lineari è dato dalle equazioni di Navier-Stokes, relative allo scorrimento di un fluido incomprimibile che aderisce alle pareti. Le equazioni alle derivate parziali non lineari compaiono anche nella teoria della geometria differenziale. Infatti, si incontrano problemi non lineari stazionari nella minimizzazione di funzionali che si esprimano mediante integrali di derivate delle funzioni incognite sotto forma non quadratica (soltanto il caso quadratico porta a un'equazione di Euler-Lagrange lineare).
La fisica utilizza sia le equazioni integrali, sia le equazioni integrali alle derivate parziali, cioè contenenti non solo derivate parziali, ma anche quelle integrali, lineari o no. A questo riguardo, il modello più noto è probabilmente quello delle equazioni di Boltzmann. Segnaliamo anche lo studio dei problemi multifasi, che conducono ai cosiddetti problemi di frontiera libera, come per esempio le equazioni di Stefan nella teoria dell'evaporazione, la teoria delle scie, ecc.
Tutte le equazioni precedenti si possono scrivere nella forma A(u)=f, dove A è un operatore, lineare o no, che applica uno spazio D(A) (il dominio di A che, nella sua definizione, tiene anche conto delle condizioni al contorno) su uno spazio F: essendo dato f∈F, si cerca u∈D(A) che la soddisfi.
Ma certe applicazioni relativamente recenti affrontate con diversa prospettiva, quali i problemi di controllo ottimale connessi con le ricerche spaziali o con il controllo di processi industriali ed economici, ovvero i problemi di meccanica unilateral' o di meccanica con condizioni di snervamento (plasticità, materiali bloccanti, ecc.) hanno portato allo studio sistematico delle equazioni del tipo A(u)=f dove A è un operatore multivoco. A(u) non è più un punto di uno spazio funzionale F, ma un suo sottoinsieme; in tal caso, si cerca u tale che f∈A(u).
Quanto è stato detto si riferisce a un universo deterministico. La necessità di superare questa limitazione ha portato alla teoria delle equazioni stocastiche e, soprattutto, alla teoria del controllo ottimale dei sistemi stocastici. Qui non insisteremo sulla teoria dei modelli o su quella dell'identificazione dei sistemi.
È certo che i progressi delle altre scienze portano automaticamente a nuovi modelli di equazioni: se ne hanno degli esempi nella biomatematica, nell'economia (dove intervengono, tra le altre, equazioni a ritardo), ecc.
Le prime questioni di carattere matematico che insorgono in relazione a un nuovo modello sono: (a) il problema è ben posto? Ammette cioè un'unica soluzione, dipendente in modo continuo dai dati (ovviamente in una topologia da precisare)? (b) Il problema è stabile? Si possono ottenere alcune proprietà delle soluzioni (una stima approssimata, il comportamento all'infinito, ecc.)? (c) È possibile calcolare numericamente la soluzione servendosi di un sistema informatico più o meno evoluto?
Definizione delle soluzioni
Tenteremo, in questo articolo, di fornire qualche indicazione sulla soluzione di alcuni dei problemi accennati nell'introduzione, raggruppando le nostre idee secondo i possibili metodi per ottenerla.
Il primo problema da affrontare, pertanto, concerne la definizione precisa di ciò che si intende per soluzione.
È naturale cominciare con il caso delle equazioni lineari alle derivate parziali senza condizioni al bordo.
In altri termini, sia P un operatore differenziale di ordine m,
[1] formula
in cui si supponga dapprima che i coefficienti pα siano differenziabili indefinitamente. Qui e nel seguito α=(α1,...,αn) è un multi-indice (αi∈ℕ), ∣α∣=∑iαi e Dα=∂α1/∂x1...∂αn/∂xn.
Ci proponiamo di considerare, dal punto di vista più generale possibile, la seguente equazione:
[2] Pu=f.
A tale scopo, conviene cercare di operare in uno spazio vettoriale topologico che sia sufficientemente grande, in modo che ogni suo elemento sia una funzione derivabile quante volte si voglia, in un senso opportuno.
Per questo si utilizza la dualità. Si introduce uno spazio 'molto piccolo': lo spazio D(ℝn)=D delle funzioni C∞ a supporto compatto in ℝn (funzioni di questo tipo esistono e sono anche assai numerose; per es., D è denso nello spazio L2(ℝn) delle funzioni a quadrato sommabile); seguendo Laurent Schwartz, si introduce in questo spazio 'molto piccolo' una topologia 'molto fine'. In tal modo una successione φj∈D tenderà a zero in D se: (a) tutte le φj hanno i loro supporti in un compatto fisso; (b) le φj, insieme a tutte le loro derivate, tendono uniformemente a zero.
Allora, per definizione, lo spazio delle distribuzioni è lo spazio duale D′ di D.
La proprietà fondamentale di una distribuzione g∈D′ per porre problemi del tipo [2], è che essa ammette derivate Dαg∈D′ per ogni ∀α.
Indichiamo perciò con 〈g,φ〉 il prodotto scalare tra g∈D′ e φ∈D, nella dualità tra D′ e D; se g è una funzione allora
[3] 〈g,φ〉=∫ℝng(x)φ(x)dx
e se g è derivabile allora
[4] formula.
Ora, se g∈D′ si prende la [4] come definizione di ∂g/∂xi. Si verifica che (∂g/∂xi)∈D′ e si definisce Dαg per ricorrenza:
[5] 〈Dαg,φ〉=(−1)∣α∣〈g,Dαφ〉.
In tal caso, se u∈D′, siamo in grado di definire Pu, e cioè poniamo
[6] pα g∈D′ per 〈pα g,φ〉=〈g,pα φ〉.
Il problema generale naturale diventa, pertanto, il seguente: per f data in D′, trovare u in D′ che sia soluzione della [2].
Ciò conduce a delle classificazioni di operatori assai interessanti: quelli per cui tutte le soluzioni sono C∞ (oppure analitiche) qualora lo sia il secondo membro; si ottiene in tal modo la classe degli operatori ipoellittici (o, rispettivamente, quella degli operatori ellittici).
Una formulazione così generale ha il grande pregio di semplificare l'enunciato dei problemi; per esempio, si deve a Hans Lewy la scoperta di certi operatori P per i quali la [2] può non avere soluzione; donde il problema: quali sono gli operatori P per i quali esistono sempre delle soluzioni in D′?
È possibile d'altronde procedere in modo assai ragionevole a un'ulteriore generalizzazione del problema, introducendo degli spazi ancora più piccoli di D, come quelli delle classi di funzioni quasi-analitiche: per esempio, lo spazio gs delle funzioni di Gevrey di ordine s>1 a supporto compatto; considerandone lo spazio duale, si ottengono le classi di ultradistribuzioni nelle quali si possono porre dei problemi analoghi ai precedenti.
Queste teorie forniscono gli strumenti per la formulazione dei problemi lineari che non hanno condizioni al bordo.
Per i problemi in cui vi siano condizioni al bordo, lo strumento principale è costituito da particolari classi di distribuzioni su un aperto Ω, quali sono gli spazi di Sobolev e i loro duali.
Indichiamo con Hm(Ω) lo spazio delle classi di funzioni v∈L2(Ω) tali che
[7] Dαv∈L2(Ω) ∀∣α∣≤m
(Dαv è calcolato nel senso delle distribuzioni su Ω); introduciamo ora nello spazio Hm(Ω) la norma hilbertiana
[8] formula.
Indichiamo con H0m(Ω) la chiusura di D(Ω) in Hm(Ω) (D(Ω) è lo spazio delle funzioni C∞ a supporto compatto in Ω) e con H−m(Ω) il duale di H0m(Ω).
Il problema di Dirichlet si può allora formulare nei termini seguenti: assegnata f in H−1(Ω), trovare una u∈H01(Ω) che sia soluzione di
[9] −Δu=f.
Questa formulazione è giustificata dal fatto che
[10] u∈H01(Ω) u∈H1(Ω) e u=0 su Γ.
Si noti che le condizioni al bordo sono state, per dir così, trasferite nelle definizioni degli spazi. Ritornando a quanto affermato a proposito dell'equazione A(u)=f, si ha
[11] D(A)=H01(Ω), F=H−1(Ω).
Gli spazi di Sobolev Hm(Ω), costruiti su L2(Ω), possono essere insufficienti per i problemi non lineari. Più spesso si introducono gli spazi di Sobolev Wm,p(Ω) su Lp(Ω), con 1≤p≤∞:
[12] Wm,p(Ω)={v tali che v∈Lp(Ω), Dαv∈Lp(Ω) ∀∣α∣≤m},
nei quali Wm,2(Ω)=Hm(Ω). In generale, se si introduce in Wm,p(Ω) la norma
[13] formula
otteniamo uno spazio riflessivo, a eccezione dei casi in cui p=1 e p=∞; la non riflessività di W1,1(Ω) è alla origine delle grandi difficoltà che si incontrano nella teoria delle superfici minime.
Si può osservare, in base a quanto esposto finora, che si perde molto in generalità passando dai problemi delle equazioni senza condizioni al bordo (che vengono posti negli spazi generali delle distribuzioni o delle ultradistribuzioni) a quelli con condizioni al bordo (in questo altro caso, i problemi sono stati posti in spazi molto particolari di distribuzioni); invero è possibile, dimostrando dapprima certe proprietà di regolarità e quindi trasponendole, risolvere i problemi al bordo lineari in spazi di distribuzioni e di ultradistribuzioni. Ciò è, invece, essenzialmente impossibile nel caso di problemi non lineari.
In conclusione, disponiamo ora degli strumenti mediante i quali diventa possibile porre in modo rigoroso i problemi di equazioni alle derivate parziali; presentiamo nel seguito alcuni dei metodi essenziali per la loro risoluzione.
Il metodo della trasformata di Fourier; operatori pseudodifferenziali; operatori integrali di Fourier
Supponiamo che P sia un operatore a coefficienti costanti, ovvero
[14] formula
a priori, il metodo più naturale per risolvere l'equazione
[15] Pu=f
consiste nell'utilizzare la trasformata di Fourier.
Per esempio, se v è una funzione sommabile su ℝn la sua trasformata di Fourier ‸v sarà la funzione data da
[16] formula.
Conviene definire, innanzi tutto, la trasformata di Fourier di una funzione o di una distribuzione, che sia più generale possibile. A tal fine, si utilizza di nuovo il concetto di dualità. Introduciamo, seguendo ancora Schwartz, lo spazio più piccolo possibile delle funzioni v tali che v e ‸v posseggano proprietà analoghe: volendo precisare questa idea, si arriva a introdurre lo spazio S=S(ℝn) delle funzioni C∞ a decrescita rapida
[17] S={v tali che xαDβv∈L2(ℝn) ∀α‚β}
che è uno spazio di Fréchet (cioè metrizzabile e completo) per la famiglia di seminorme
[18] pαβ(v)=∥xαDβv∥L2(ℝn).
Si dimostra allora facilmente che v→‸v è un isomorfismo
[19] formula.
Introduciamo allora lo spazio S′ duale di S, che è lo spazio delle distribuzioni a crescita lenta. Definiamo, quindi, la trasformata di Fourier f‸ di f ∈S′ per trasposizione:
[20] formula.
Tale definizione è giustificata dal fatto che, se f è per esempio una funzione sommabile, allora:
[21] formula.
L'applicazione f→f‸ è un isomorfismo S′→S′. Scriveremo ancora formalmente (indicando le distribuzioni come funzioni)
[22] formula
e avremo la formula d'inversione
[23] formula.
Utilizziamo ora questo strumento fondamentale per risolvere il problema [15], in cui si precisa che f è data in S′ e che si cerca u in S′.
La trasformata di Fourier di ∂u/∂xj è iξjû, così che, se si pone
[24] formula
allora la [15] equivale a
[25] formula.
Il polinomio P(ξ) (uguale alla trasformata di Fourier di Pδ, dove δ è la densità di massa nell'origine o δ di Dirac) è il simbolo dell'operatore P. Formalmente, la soluzione della [25] è evidente:
[26] formula
da essa, utilizzando la formula di inversione [23], si ricava l'espressione
[27] formula.
Naturalmente, vi sono difficoltà tanto maggiori quanto maggiore è la varietà delle ξ reali per le quali P(ξ)=0. Così non vi è alcuna difficoltà se
[28] P=−Δ+identità,
perché in tal caso la [27] dà
[29] formula.
È tuttavia possibile adattare la [27] integrando nello spazio complesso ed evitando così la varietà P(ξ)=0. In tal modo si giunge a dimostrare che per ogni f in D′ (e non più solo in S′) esiste u in D′ soluzione della [15].
In particolare, esiste una distribuzione E soluzione di
[30] PE=δ.
In tal caso si dice che E è soluzione elementare di P. È possibile classificare gli operatori P a partire dalle proprietà delle soluzioni elementari. Perciò, dire che P è ellittico (oppure ipoellittico) equivale a dire che esiste una soluzione elementare analitica (oppure C∞) al di fuori dell'origine (poiché δ è nulla fuori dell'origine). Un problema interessante, in cui interviene la geometria algebrica, consiste allora nel caratterizzare mediante le proprietà del polinomio P(ξ) la proprietà di ipoellitticità. Tale problema è stato risolto da Lars Hörmander nel 1955.
Allo stesso modo si possono introdurre gli operatori iperbolici che sono, all'incirca, gli operatori P che ammettono una soluzione elementare con supporto entro un cono strettamente convesso. Si verifica facilmente, allora, che l'operatore (∂2/∂t2)−Δ è iperbolico: esso ammette una soluzione elementare con supporto entro il cono K={∣x∣≤t, con t>0}. È noto ed è facile da verificare che uno studio più preciso del supporto della soluzione elementare di (∂2/∂t2)−Δ fa intervenire la dimensione dello spazio: se essa è dispari il supporto è costituito dalla frontiera del cono K, mentre è tutto il cono K se la dimensione è pari. Tale proprietà è fondamentale per le applicazioni in fisica; su di essa si fonda, per esempio, il fenomeno della propagazione delle onde in tre dimensioni.
Nelle applicazioni, per esempio in geofisica, si incontrano dei sistemi iperbolici per i quali è importante conoscere le proprietà del supporto di una soluzione elementare. È questo il problema generale della teoria delle lacune: si tratta di trovare, a partire dalle proprietà algebriche di P(ξ) o di un sistema di polinomi), le proprietà dei 'buchi' del supporto di una soluzione elementare. Successivamente ai lavori di Ivan G. Petrowski del 1936, questa teoria è stata sviluppata e approfondita da Michael Atiyah, Raoul Bott e Lars Gårding (1970).
Segnaliamo, inoltre, il fatto che si possono studiare sistemi del tipo
[31] Piu=fi, i=1,…,N
che intervengono per esempio nella teoria delle funzioni di più variabili complesse. Naturalmente, affinché il problema possa ammettere una soluzione, i dati f devono soddisfare delle condizioni di compatibilità del tipo Pjfi=Pjfi ∀i,j. La soluzione di questi problemi dipende in larga misura da proprietà di geometria algebrica.
Riassumendo, l'algoritmo costituito dalla trasformata di Fourier fornisce gli elementi necessari per la soluzione delle equazioni generali lineari a coefficienti costanti, senza condizioni al bordo.
Per tener conto delle condizioni al bordo, si consideri il problema seguente:
[32] Pu=f in Ω, Bju=gj su Γ
dove P e Bj sono degli operatori a coefficienti costanti e Ω è il semispazio definito da {x tali che xn>0}. Si effettui una trasformata di Fourier nelle variabili tangenziali x1,…,xn−1; il problema [32] si riduce allora a un'equazione differenziale ordinaria nella variabile xn, nella quale la variabile ξ={ξ1,…,ξn−1} funge da parametro, con condizioni al bordo per xn=0 e condizioni di decrescenza per xn→+∞ che dipendono anch'esse dal parametro. Si perviene così a certe condizioni (algebriche), che devono essere soddisfatte dal sistema {P,Bj}; esse sono necessarie e sufficienti affinché il problema [32] sia posto in modo corretto e si sogliono indicare col nome di condizioni di Lopatinski-Shapiro.
Ciò permette allora di risolvere il problema ellittico generale (lineare): si consideri in un aperto Ω un operatore ellittico A di ordine 2m a coefficienti variabili con sufficiente regolarità. Siano inoltre Bj operatori di ordine minore o uguale a 2m−1. Il problema consiste nel trovare, in modo conveniente, una soluzione di
[33] Au=f, Bju=gj su Γ.
Mediante mappe locali e partizioni dell'unità, ci si riduce al problema [32] per operatori a coefficienti variabili. Fissando i coefficienti in un punto x0 qualunque del bordo, si scrivono le condizioni di Lopatinski-Shapiro in tale punto x0; quindi, facendolo variare, si ottengono le condizioni necessarie e sufficienti affinché il problema [33] sia posto correttamente (ciò consente di risolvere il problema negli spazi di Sobolev costruiti su L2 e, con l'ausilio inoltre della teoria di Calderon-Zygmund-Michlin sugli integrali singolari, anche negli spazi di Sobolev costruiti su Lp, 1〈p〈∞).
Se Ω è un aperto limitato, il nucleo N dell'operatore A per condizioni al bordo Bju=0, cioè
[34] N={u tali che Au=0, Bju=0 su Γ, ∀j}
ha dimensione finita, al pari del nucleo N* del problema aggiunto. L'indice del problema è χ=dim N−dim N*. La questione riguardante l'invarianza dell'indice per differenti modifiche del problema è stato risolto da Atiyah e Isadore Singer nel 1963, poi da Atiyah e Bott nel 1964, mediante l'impiego contemporaneo di risultati di analisi e di topologia. Uno strumento importante, per la grandissima flessibilità che introduce nelle modifiche da apportare a un dato operatore, è costituito dagli operatori pseudo-differenziali.
Se si vogliono estendere le considerazioni svolte all'inizio di questo capitolo agli operatori a coefficienti variabili
[35] formula
si è portati a introdurre il simbolo di P
[36] formula
e a considerare in modo del tutto generale gli operatori pseudodifferenziali
[37] formula
dove a si comporta come somma di funzioni omogenee per ∣ξ∣→∞. Si può estendere completamente la teoria dei problemi al bordo ellittici, sostituendo gli operatori differenziali con opportuni operatori pseudodifferenziali. Soprattutto, è possibile compiere un passo avanti decisivo nella generalizzazione degli operatori differenziali facendo ricorso alla cosiddetta teoria degli operatori integrali di Fourier, sviluppata da Hörmander e Viktor G. Maslov.
Questa teoria, sviluppata da Hörmander tra il 1969 e il 1970, si adatta sostanzialmente allo studio di operatori non ipoellittici con metodi simili a quelli classici delle trasformate di Fourier. Il loro uso fa intervenire la teoria classica delle caratteristiche e delle bicaratteristiche.
Questi operatori sono legati anche alla teoria degli sviluppi asintotici e trovano utile impiego, mediante una equazione iperbolica, nello studio delle proprietà asintotiche degli autovalori degli operatori ellittici.
Sostanzialmente, quindi, il metodo della trasformata di Fourier con le sue notevoli generalizzazioni è lo strumento di base per la soluzione dei problemi lineari di equazioni alle derivate parziali. Altri strumenti sono indispensabili per lo studio di problemi non lineari.
I problemi di evoluzione
Fin qui abbiamo voluto dare un'idea della teoria dei problemi al bordo non lineari stazionari. Passiamo ora ai problemi di evoluzione.
Nel caso dei problemi lineari, si deve a Fourier l'osservazione classica secondo cui, se si utilizzano le autofunzioni della parte ellittica dell'operatore, il problema si riduce a dei sistemi di equazioni differenziali ordinarie. Si deve a Boris G. Galerkin l'osservazione che può anche essere conveniente, invece, servirsi di una base di funzioni qualsiasi piuttosto che di autofunzioni.
Si consideri il caso delle equazioni di Navier-Stokes. Se u={u1,…,un} rappresenta il vettore velocità e p la pressione, il sistema di equazioni sarà
[38] formula
dove u0 è dato in Ω⊂ℝn. La grandezza ν, che rappresenta la viscosità, è positiva.
Allora, se Vm indica un sottospazio di V di dimensione finita m, si dimostra, mediante una serie di opportune valutazioni a priori e l'uso di teoremi di compattezza, che um data da
[39] formula
converge in modo opportuno verso una soluzione u del problema di Navier-Stokes. A tal proposito va ricordato che, anche dopo i lavori classici di Jean Leray e quelli più recenti di numerosi ricercatori in diverse direzioni, il problema fondamentale dell'idrodinamica non è stato ancora completamente risolto: se la dimensione dello spazio è uguale a due si conoscono parecchie classi funzionali per le quali si è dimostrata l'esistenza e l'unicità della soluzione, ma il problema analogo in spazi a tre dimensioni è ancora aperto; si conoscono alcune classi funzionali in cui si ha l'esistenza ma non si sa nulla sull'unicità, e viceversa. Analogamente, il problema del comportamento delle soluzioni quando la viscosità tende a zero, fondamentale nell'idrodinamica applicata, resta ancora aperto.
Nel caso in cui l'equazione di evoluzione, lineare o no,
[40] formula
ammetta un'unica soluzione opportuna, allora l'applicazione
[41] u0→u(t)=G(t)(u0)
definisce un semigruppo lineare o no.
Nel caso lineare si può scrivere formalmente
[42] G(t)u0=e−tAu0
e l'operatore A si comporta come il generatore infinitesimale del semigruppo: in un senso opportuno, si ha
[43] formula
Diviene allora naturale tentare di invertire il ragionamento e di trovare a priori le condizioni necessarie e sufficienti affinché A sia generatore di un semigruppo. Naturalmente esistono nozioni diverse di semigruppo: i semigruppi più generali sono quelli di distribuzioni o di ultradistribuzioni, ma in questo contesto ci si riferirà ai semigruppi continui. La teoria di Hille-Yosida fornisce, appunto nel caso di un semigruppo continuo, le suddette condizioni necessarie e sufficienti, espresse mediante le proprietà dello spettro di A.
Nelle applicazioni sarà quindi sufficiente verificare che un dato operatore differenziale A soddisfi le proprietà del teorema di Hille-Yosida. Si è potuta estendere la teoria anche in alcuni dei casi in cui l'operatore A dipende da t.
La teoria dei semigruppi è molto utile anche nella teoria delle probabilità, per esempio nello studio dei semigruppi di Markov. Si devono segnalare soprattutto le recenti estensioni della teoria al caso di problemi non lineari; la teoria dei semigruppi non lineari è ancora in pieno sviluppo.
Naturalmente, se si ritorna al caso lineare, la teoria dei semigruppi è legata a quella della trasformata di Laplace. Utilizzando la trasformata di Laplace nel senso delle distribuzioni, si è potuto dimostrare che tutti i problemi di evoluzione lineare ben posti possono essere risolti mediante la trasformata di Laplace in t.
Segnaliamo ancora un'estensione della teoria lineare delle equazioni di evoluzione
[44] formula
a una situazione più generale, in cui intervengono equazioni operazionali del tipo
[45] Bu+Au=f
in cui A e B sono operatori non limitati che soddisfano opportune proprietà spettrali.
Infine ricordiamo l'estensione, utile nella teoria del controllo ottimale dei sistemi retti da equazioni alle derivate parziali e in certi problemi di fisica quantistica, della teoria dei semigruppi al caso in cui gli elementi u(t) della funzione incognita siano in un'algebra.
Metodi di approssimazione
Abbiamo già avuto occasione di incontrare, a proposito della [39], un metodo di approssimazione: l'equazione alle derivate parziali non lineare da risolvere è stata approssimata con un sistema di equazioni differenziali.
Per poter utilizzare i calcolatori elettronici, è necessario invece approssimare la soluzione cercata mediante certe soluzioni di equazioni algebriche.
Prendiamo in considerazione per primo il caso stazionario. Nel caso lineare, il metodo di approssimazione più classico della soluzione di
[46] Au=f
con opportune condizioni al bordo, consiste nel sostituire alle derivate parziali dei rapporti incrementali: è questo il metodo delle differenze finite. Naturalmente si può approssimare una data derivata con una infinità di rapporti incrementali, facendo intervenire un numero più o meno grande di punti del reticolo discreto sul quale ci si pone. Si ha, dunque, a priori una infinità di schemi possibili con differenze finite: per la scelta dello schema, sia
[47] Ahuh=fh
(dove h sta a indicare un parametro a una o più dimensioni che serve a individuare il reticolo di discretizzazione); si deve verificare naturalmente che il problema algebrico [47] ammette un'unica soluzione e quindi verificare che lo schema è convergente verso la soluzione u della [46]. Tra i diversi schemi convergenti, la scelta ‒ che può anche essere difficile ‒ deve tenere conto della stima dell'errore, della facilità di definire lo schema stesso e della natura più o meno semplice della matrice Ah. Nei casi non lineari, dopo aver discretizzato, bisogna ricorrere a metodi iterativi di linarizzazione.
I problemi di evoluzione, in generale, vengono trattati dal punto di vista numerico mediante discretizzazione delle variabili spaziali e temporali. Se si deve risolvere
[48] formula
si introduce un passo temporale Δt; sia unh l'approssimazione di u all'istante n Δt. Allora, se Ah è costruito a partire da A mediante il metodo delle differenze finite o quello degli elementi finiti, alla [48] si può sostituire
[49] formula
oppure
[50] formula(
evidentemente esiste un'infinità di modi possibili). Alla [49] o alla [50] si deve aggiungere il dato iniziale
[51] formula.
Per attuare lo schema [50], ovvero per passare da uhn a uhn+1, si deve risolvere l'equazione
[52] uhn+1+ΔtAh(uhn+1)=uhn+Δtfhn+1
a motivo della quale lo schema [49] si dice implicito.
Analogamente la [50] fornisce esplicitamente uhn+1 a partire da uhn:
[53] uhn+1=uhn+Δt(fhn−Ah(uhn)).
Lo schema [50] si dice esplicito. Non se ne deve, tuttavia, dedurre affrettatamente che lo schema [50] debba essere sistematicamente preferito al [49]. Invero si dimostra che in molte classi di problemi lo schema [49] è convergente quando h e Δt tendono a zero indipendentemente, mentre lo schema [50] è convergente solo se h e Δt tendono a zero verificando una condizione detta di stabilità.
Gli schemi impliciti permettono di avanzare nel tempo scegliendo dei grandi intervalli Δt (naturalmente tali intervalli di tempo possono essere variabili) al prezzo della difficoltà essenziale di risolvere la [52], mentre gli schemi espliciti, che possono essere trattati con maggiore facilità, possono richiedere degli intervalli Δt molto più piccoli.
Sorge allora spontanea l'idea di conservare la buona convergenza dei metodi impliciti, ma di semplificare la risoluzione della [52] o di una equazione analoga. Si arriva così a uno dei metodi di decomposizione che rappresenta una delle idee fondamentali dell'analisi numerica: l'operatore A viene scomposto in parti elementari.
[54] A(u)=A1(u)+A2(u)
dove ogni Ai è più semplice di A. Questo metodo può essere di grande aiuto nelle applicazioni, ed è invero molto spesso utilizzato implicitamente dai fisici e dagli ingegneri quando si prendono in considerazione successivamente, e non simultaneamente, i diversi fenomeni fisici che intervengono in un problema. D'altra parte, dal momento che ogni teoria dell'approssimazione introduce degli errori sistematici, si può benissimo aggiungere, cambiando il tipo di equazione, un errore a priori per ottenere un'equazione più semplice. In verità, per risolvere un dato problema si può scegliere tra un gran numero di metodi numerici: i criteri di scelta dovrebbero basarsi sulla stima della quantità di calcolo, dovendosi un metodo ritenere soddisfacente quando è assai vicino alla quantità ottimale di calcolo. È stato possibile raggiungere risultati parziali in questa importante direzione grazie al concetto di entropia di Andreij N. Kolmogorov.
Bibliografia
Atiyah 1970: Atiyah, Michael - Bott, Raoul - Gårding, Lars, Lacunas for hyperbolic differential operators, "Acta mathematica", 124, 1970, pp. 109-189.
Hörmander 1964: Hörmander, Lars, Linear partial differential operators, 2. ed., Berlin, Springer, 1964.
Leray 1934: Leray, Jean, Essai sur le mouvement plan d'un liquide visqueux que limitent des parois, "Journal de mathématiques pures et appliquées", 13, 1934, pp. 331-418.
Leray, Schauder 1934: Leray, Jean - Schauder, Juliusz, Topologie et équations fonctionnelles, "Annales de l'École Normale Supérieure", 51, 1934, pp. 45-78