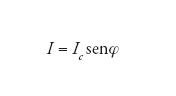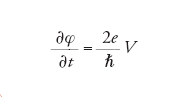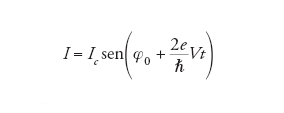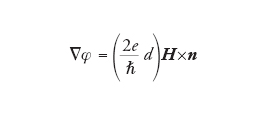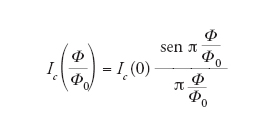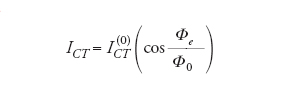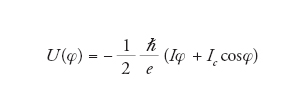Giunzioni Josephson
Giunzioni Josephson
Alla fine degli anni Cinquanta del XX sec. fu studiato il tunnel di singoli elettroni in giunzioni costituite da due film metallici separati da una barriera di ossido sottile (dello spessore di alcuni nanometri). La caratteristica corrente-tensione (I-V) risulta , in tal caso, lineare per basse tensioni (dell'ordine dei millivolt). Ciò è spiegato con una semplice applicazione della regola d'oro di Fermi e fu osservato sperimentalmente nel 1960 da Ivar Giaevier, il quale, utilizzando i risultati della teoria BCS (dalle iniziali degli autori, John Bardeen, Leon N. Cooper e John R. Schrieffer), estese il modello fenomenologico al tunnel tra superconduttori e ne sviluppò lo studio sperimentale. Il risultato per T>Tc (Tc, temperatura critica del superconduttore) indicava naturalmente l'andamento ohmico prima visto, laddove per T〈Tc (tunnel superconduttore-superconduttore) si osservava una caratteristica I-V fortemente non lineare, correlata alla presenza dei gap di energia negli spettri di eccitazione di quasi-particelle dei superconduttori.
L'esistenza e la rilevanza del possibile effetto tunnel di coppie di Cooper affascinò Brian D. Josephson, giovane studente del Cavendish Laboratory di Cambridge, che vi si dedicò con grande passione. L'analisi teorica sviluppata da Josephson dimostrò la possibilità di un accoppiamento debole tra due superconduttori in una giunzione tunnel con barriera estremamente sottile (dell'ordine di 1 nm), fornendo le equazioni che ne descrivono completamente l'elettrodinamica. Nel 1973 Josephson, con Giaevier e Leo Esaki, fu premiato con il Nobel per la fisica per le ricerche sperimentali sull'effetto tunnel.
Un superconduttore può essere descritto mediante una funzione d'onda macroscopica del tipo Ψ=ϱ1/2eiφ, dove ϱ=∣Ψ∣2 rappresenta la densità delle coppie di Cooper e φ la fase. Il numero totale di coppie N e la fase sono variabili coniugate che obbediscono a una relazione di indeterminazione del tipo ΔNΔφ≈2π. Ciò esprime la circostanza che in un singolo superconduttore isolato, per il quale cioè il numero N delle coppie di Cooper è costante, N è fisso e di conseguenza φ totalmente indeterminata.
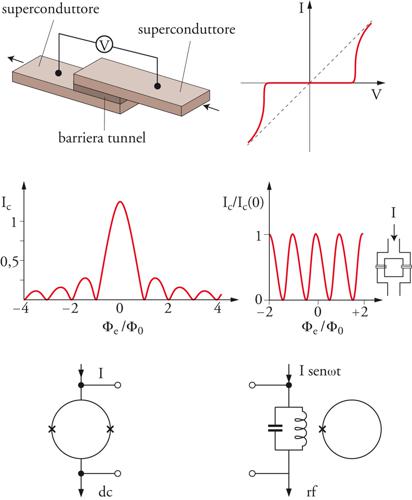
Consideriamo ora un sistema di due superconduttori S1 e S2 (descritti rispettivamente da Ψ1=√ϱ1 eiφ1 e Ψ2=√ϱ2 eiφ2) posti estremamente vicini, a una distanza di circa 1 nm. Ciò può essere realizzato mediante una giunzione S1-I-S2, in cui I rappresenta una barriera tunnel di materiale dielettrico. L'intuizione di Josephson fu appunto quella di prevedere che una struttura di questo tipo avrebbe consentito una sovrapposizione delle due funzioni d'onda macroscopiche Ψ1 e Ψ2, realizzando così un accoppiamento debole tra i due superconduttori. Se l'energia coinvolta in tale accoppiamento è maggiore di quella dovuta alle fluttuazioni termiche, si stabilisce una correlazione di fase tra i due superconduttori, che consente il passaggio delle coppie di Cooper da un superconduttore all'altro attraverso la barriera (Cooper pairs tunneling). In tal modo si ha quindi la possibilità del fluire di una supercorrente tra i due superconduttori, funzione della fase relativa φ1−φ2=φ. Il sistema (giunzione) dei due superconduttori accoppiati si comporta, in una certa misura, come un unico superconduttore.
Le equazioni costitutive dell'effetto Josephson
Le equazioni a cui perviene la teoria di Josephson in termini di relazioni corrente-fase, I(φ), e tensione-fase, V(φ), sono:
[1a] formula;
[1b] formula
dove Ic indica la supercorrente critica. Si vede che V=0 implica φ=cost e quindi la possibilità di una corrente continua che fluisce attraverso la struttura con caduta di potenziale nulla. È questo in sostanza l'effetto Josephson in corrente continua (fig. 2B). Se consideriamo V≠0, integrando la [1b] e sostituendo nella [1a], si ottiene
[2] formula.
Si ha cioè una corrente alternata con frequenza ν=2eV/ℏ (rapporto frequenza tensione ν/V=483,6 MHz/μV), che rappresenta l'effetto Josephson in corrente alternata. La rivelazione di tale effetto può ottenersi sottoponendo la giunzione a radiazione con opportuna frequenza ν e osservando le risonanze che si manifestano nella caratteristica I-V come gradini di tensione a valori Vn=(nh/2e)ν. L'equazione [1b] indica la modulazione temporale della fase da parte della tensione. Si può altresì ottenere una modulazione spaziale della fase mediante l'applicazione di un campo magnetico H:
[3] formula.
dove d=(t+λL1+λL2), t è lo spessore della barriera, λL la penetrazione di London e n il vettore unitario normale al piano della giunzione.
Ricordiamo che, dalle relazioni riguardanti l'effetto Josephson e equazioni di Maxwell, si ha un'equazione non lineare che con opportune normalizzazioni può scriversi (in una dimensione) nella forma φxx−φtt=senφ, nota come equazione Sine-Gordon. Le soluzioni solitoniche di tale equazione corrispondono ai flussoni di Josephson. Nelle Josephson, la dinamica di tali flussoni è di rilevante interesse anche in ambiti che trascendono il campo della superconduttività.
Può essere dimostrato che, nel caso stazionario, la dipendenza della corrente critica dal campo magnetico applicato è funzione della geometria della giunzione. Nel caso di giunzioni rettangolari si ottiene, in termini di flusso Φ che attraversa la giunzione, una dipendenza I-Φ di tipo Fraunhofer (fig. 2C):
[4] formula
con Φ0=hc/2e detto quanto di flusso (pari a 2,07×10−7 G∙cm2).
Questo risultato è conseguenza della natura ondulatoria del parametro d'ordine in un superconduttore. Insieme a tale fenomeno diffrattivo possono aversi fenomeni interferenziali. In particolare, se consideriamo due giunzioni Josephson in parallelo chiuse da un circuito superconduttivo, la dipendenza supercorrente-flusso riprodurrà un andamento interferenziale del tipo (fig. 2D):
[5] formula
dove ICT è la corrente totale attraverso il parallelo delle due giunzioni (assumendo IC1=IC2) e Φe/Φ0 è il flusso concatenato al circuito superconduttivo, con Φe flusso esterno; il quanto di flusso Φ0 determina la periodicità. La possibilità di misurare piccolissime frazioni di Φ0 è alla base dell'impiego di tali strutture superconduttive interferometriche, dette SQUID (Superconducting quantum interference device), per la misura di campi magnetici estremamente flebili.
Giunzioni Josephson a bassa e ad alta temperatura critica
È importante osservare che la struttura tunnel per una giunzione è la configurazione archetipo di una giunzione Josephson. Tuttavia, si possono pensare altre strutture in cui l'accoppiamento debole tra i due superconduttori viene realizzato in maniera diversa. Ciò che è necessario perché si abbia l'effetto Josephson è la sovrapposizione non nulla delle funzioni d'onda macroscopiche Ψ1 e Ψ2.
Le giunzioni Josephson basate su superconduttori tradizionali (a bassa temperatura critica) sono ottenute mediante deposizione sotto vuoto spinto di un primo film superconduttore; si realizza poi la barriera di tunnel, costituita da materiale dielettrico (con uno spessore dell'ordine di 1 nm) e quindi la deposizione del secondo elettrodo superconduttore. La barriera di tunnel può essere ottenuta mediante ossidazione del primo film superconduttore. Naturalmente, si tratta soltanto di una descrizione schematica; in realtà la scelta del materiale, l'adeguata tecnica di deposizione, la definizione della geometria della giunzione, i problemi relativi al wiring, ecc., sono tutti aspetti di rilevante importanza. Ulteriori problemi tecnologici riguardano la realizzazione di strutture complesse che utilizzano tali giunzioni (dette array di giunzioni) e in generale l'integrazione di circuiti superconduttivi.
La scoperta della superconduttività ad alta temperatura critica ha aperto un ulteriore capitolo anche nel contesto delle strutture Josephson. Nel caso delle giunzioni basate sui superconduttori ad alta temperatura critica, il piccolo valore della lunghezza di coerenza in tali materiali non consente in pratica di ottenere affidabili strutture tunnel a sandwich del tipo visto per i superconduttori convenzionali. Sono state realizzate strutture Josephson in varie configurazioni. Di maggiore interesse sono le giunzioni biepitassiali e a bicristallo. Tali strutture consentono configurazioni di fondamentale importanza per il ruolo che ha la simmetria non convenzionale del parametro d'ordine in tali classi di superconduttori. Va ricordato che l'effetto Josephson costituisce un insostituibile strumento di indagine proprio di tali aspetti fondamentali della fisica dei superconduttori ad alta temperatura critica e di altre classi di superconduttori non convenzionali.
Attivazione termica e tunnel quantistico macroscopico
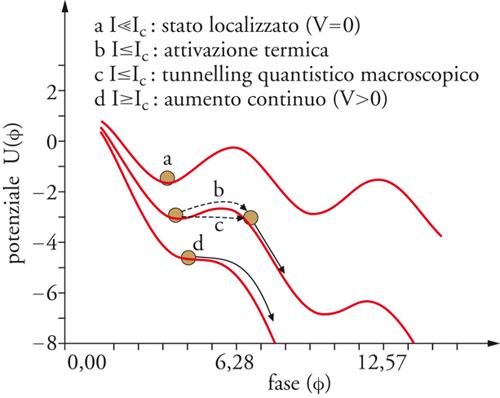
Il comportamento di una giunzione Josephson può essere descritto mediante un'energia potenziale, funzione della fase relativa, data da
[6] formula
e avente l'andamento riportato in fig. 3 curva a. La pendenza media di tale potenziale washboard è data dalla corrente di alimentazione. La posizione della fase di U(φ) può essere descritta, in analogia meccanica, come quella di una particella di massa m. Riferendoci alle equazioni [1a] e [1b], in tale analogia la posizione della particella in un minimo di U(φ) corrisponde a un valore costante della fase e pertanto allo stato della giunzione a tensione nulla. Aumentando la corrente di alimentazione, aumenta la pendenza della U(φ) e progressivamente si riduce l'altezza della barriera di potenziale fino ad annullarsi per I=Ic e, per I>Ic, producendo lo scorrimento della particella verso il basso (curva d). Conseguentemente, φ cambierà nel tempo determinando così (equazione [1b]) lo stato di tensione finita nella giunzione.
Naturalmente, per valori di corrente di polarizzazione prossimi al valore critico Ic, le fluttuazioni termiche possono, con il loro contributo energetico kT, consentire alla particella di superare la barriera di potenziale (curva b). La probabilità di tale attivazione termica può esprimersi, secondo la teoria classica di Kramer, come P=A0exp(−ΔU/kT), dove ΔU è l'altezza della barriera di potenziale che, come abbiamo visto, dipende dalla corrente di bias. L'espressione del prefattore A0 è funzione dei vari regimi di damping.
Particolarmente intrigante è la possibilità di un'attivazione quantistica (curva c), cioè di un tunnel quantistico macroscopico (MQT, Macroscopic quantum tunneling), il cui carattere deriva dalla natura stessa della variabile φ. Questa probabilità di tunnel è data da Pq=Aexp(−B), dove A=ωϱ/2π e B=7,2ΔU/ℏωϱ. Di grande importanza è la presenza, in tale tunnel quantistico macroscopico, della dissipazione.
È interessante ricordare che il tunnel quantistico su scala macroscopica è stato invocato nel contesto cosmologico in relazione al cosiddetto destino dei falsi vuoti. Si può immaginare un Universo che dopo il big bang sia in un minimo relativo e sufficientemente freddo da non poter subire attivazione termica. Si può pensare allora a uno stato quantisticamente instabile e alla penetrazione della barriera, come una sorta di non auspicabile small bang, verso uno stato più stabile. L'esistenza di livelli energetici quantizzati e il fenomeno di tale MQT previsto da P.W. Anderson sono stati osservati e ampiamente studiati in giunzioni Josephson. Recentemente si è osservato il fenomeno del MQT e la quantizzazione dei livelli anche in giunzioni Josephson ad alta temperatura critica.
Dispositivistica superconduttiva Josephson
L'elettronica superconduttiva e le sue implicazioni sono cruciali in ambiti quali la componentistica attiva e passiva, le circuitistiche complesse e una variegata tipologia di applicazioni. Molto ampia e sofisticata è la varietà del design e delle tecnologie impiegate. Nel seguito, tuttavia, verranno discusse solo alcune classi di dispositivi che si basano sull'effetto Josephson. Dal punto di vista applicativo, l'impiego delle giunzioni Josephson investe vari campi, che vanno dalla metrologia ai rivelatori di radiazione e più in generale una stimolante nuova elettronica che sfrutta le caratteristiche proprie dei dispositivi superconduttivi: alta velocità, bassa dissipazione e bassa dispersione.
In tale contesto grande attenzione è rivolta alla circuitistica elettronica SFQ (Single flux quantum). I vantaggi propri della tecnologia di circuiti integrati basati su semiconduttore e i limiti intrinseci dovuti all'elevata dissipazione hanno suggerito anche una possibile combinazione di circuitistiche ibride semiconduttore-superconduttore. Di grande importanza è anche lo sviluppo di sensori basati sull'effetto Josephson, con particolare riferimento ai rivelatori e alle applicazioni degli SQUID.
La presenza di un gap nello spettro di eccitazione dei superconduttori è stata sempre considerata un elemento chiave per ridurre i fenomeni dissipativi e favorire la coerenza dello stato superconduttivo, aumentandone i tempi di coerenza di fase. Questi elementi sono stati anche l'origine di una serie di esperimenti basati su giunzioni con superconduttori a bassa temperatura critica, che avevano come obiettivo fondamentale la dimostrazione dei principî primi del qubit (bit quantistico) e che sono ampiamente riportati in letteratura. Vi sono anche proposte di qubit con superconduttori ad alta temperatura critica, che sfruttano le proprietà uniche di tali materiali e in particolare l'anisotropia del parametro d'ordine tipo onda d, che consente di ottenere uno stato naturalmente degenere ‒ quiet qubit ‒ senza utilizzare i campi magnetici esterni richiesti nel design dei qubit con superconduttori a bassa temperatura critica. Un parametro d'ordine tipo onda d ha per converso alimentato preoccupazioni che la presenza di quasi-particelle con bassa energia generasse dissipazione, ostacolando uno stato quantistico macroscopico. In tal senso, la recente osservazione del MQT e dei livelli quantistici di energia in giunzioni con superconduttori ad alta temperatura critica potrebbe aprire nuove prospettive.
Un'interessante classe di dispositivi superconduttivi è costituita dai rivelatori di radiazione. Le giunzioni tunnel Josephson, grazie alla loro sottilissima barriera tunnel, consentono di contare efficacemente gli elettroni prodotti dalla rottura delle coppie di Cooper da parte della radiazione incidente, il cui numero è direttamente proporzionale all'energia rilasciata nel rivelatore. Ciò si ottiene infatti sopprimendo con un campo magnetico la corrente critica e facendo lavorare la giunzione nel regime di tunnel di singola quasi-particella. Si realizzano rivelatori con le giunzioni tunnel superconduttive non solo ad alta risoluzione energetica, ma anche in grado di offrire una discriminazione temporale con risoluzione dell'ordine dei nanosecondi. Tali caratteristiche rendono le giunzioni Josephson interessanti anche in contesti applicativi quali la spettrometria di massa a tempo di volo, per misurare la massa e la funzionalità di macromolecole, come frammenti di DNA e proteine, di grande interesse in biologia (genomica e proteomica). Tale uso di rivelatori superconduttori, proposto da Damian Twerenbold, è stato dimostrato in esperimenti condotti in collaborazione con il NIST (National Institute of Standards and Technology) di Boulder, Colorado (Stati Uniti). Con tali rivelatori superconduttori si è potuto contare l'arrivo di macromolecole di massa fino al milione di unità atomiche. Sono stati sviluppati in tale contesto dispositivi che impiegano due giunzioni Josephson accoppiate elettronicamente, rivelatori duali capaci di ottenere insieme elevate risoluzioni temporali ed energetiche.
Sensori SQUID
Nello sviluppo di nuovi sensori di campi e flussi magnetici, un ruolo fondamentale è ascrivibile agli SQUID. Attualmente, tali dispositivi sono i più sensibili rilevatori di campo magnetico; ciò li ha resi indispensabili in molte applicazioni pratiche, quali il biomagnetismo, la geofisica, l'analisi non distruttiva di materiali, e in esperimenti di fisica di base, quali la rilevazione di onde gravitazionali, gli effetti quantistici macroscopici, ecc.
Il cuore di uno SQUID è costituito da un interferometro, consistente in un anello superconduttore interrotto da due giunzioni Josephson. In realtà gli SQUID possono essere realizzati con due giunzioni Josephson (dc SQUID) o con una sola giunzione (rf SQUID). Nel seguito si discuterà solo la prima classe di dispositivi, il cui impiego negli ultimi anni, grazie a una migliore sensibilità e stabilità, è stato senza dubbio prevalente. La sensibilità degli SQUID è una frazione del quanto di flusso elementare, generalmente 10−5÷10−6 Φ0. Tali dispositivi possono operare in una banda di frequenza compresa tra 200 e 300 MHz. La minima variazione di energia che può essere rivelata risulta essere dell'ordine di 2×10−34 JHz−1, valore prossimo al limite fissato dal principio di indeterminazione di Heisenberg. Tipicamente, i sensori SQUID in configurazione magnetometrica sono caratterizzati dalla presenza di un circuito di rivelazione, noto anche come trasformatore di flusso, consistente in bobine superconduttrici che rivelano il campo magnetico esterno e lo trasferiscono allo SQUID tramite un accoppiamento induttivo. In particolare, la presenza di un campo magnetico esterno genera, per effetto Meissner nella bobina principale di rivelazione, detta di pick-up, una corrente di schermaggio che scorre in un'altra bobina a forma di spirale, posta in serie alla prima e accoppiata induttivamente all'interferometro. In tal modo la corrente di schermaggio produce un flusso magnetico nello SQUID tradotto in tensione.
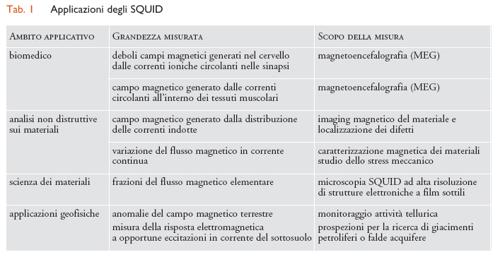
È possibile misurare campi magnetici la cui intensità è pari a circa 10−16 tesla. Per ottenere una risposta lineare e minimizzare il rumore introdotto dall'elettronica di lettura del dispositivo, vengono usati complessi schemi di misura, che richiedono la presenza di bobine e resistori a stretto contatto con il chip superconduttore; ciò rende difficile per tali sensori il grado di impacchettamento necessario in sistemi multicanale di grande complessità, quali per esempio i sistemi per magnetoencefalografia, che utilizzano un numero di sensori superiore a 100. È diventato pertanto necessario lo sviluppo di sensori SQUID completamente integrati. Gli SQUID vengono realizzati con le tecniche di deposizione dei film sottili (sputtering, laser ablation, electron beam evaporation), in modo analogo alla realizzazione dei dispositivi elettronici a semiconduttore. I materiali utilizzati per la fabbricazione del film superconduttore determinano le proprietà elettroniche dei dispositivi e la loro sensibilità. Attualmente, i superconduttori più utilizzati per la realizzazione degli SQUID sono il niobio (temperatura di transizione, 9,2 K) e il composto ceramico YBa2Cu3O7−x (temperatura di transizione, 92 K). I primi, a bassa temperatura di transizione, detti LTS SQUID (Low temperature semiconductors), raggiungono sensibilità al campo magnetico di pochi femtotesla, mentre quelli ad alta temperatura di transizione, detti HTS SQUID (High temperature semiconductors), mostrano una sensibilità di 20÷30 femtotesla. Tipicamente, le giunzioni Josephson negli LTS SQUID sono di tipo tunnel, mentre negli HTS SQUID sono di tipo ramp-edge e biepitassiali. Nella tab.1 sono riportate alcune principali applicazioni degli SQUID.
Biomagnetismo
I dispositivi SQUID hanno grande rilevanza nello sviluppo di sensori per applicazioni biomediche. Tale strumentazione è in grado di rilevare i flebili campi magnetici generati dalle correnti elettriche responsabili del funzionamento di sistemi biologici. Tecniche di biomagnetismo sono impiegate per lo studio sia dell'attività normale sia di quella patologica del corpo umano. Per le applicazioni diagnostiche relative all'apparato cardiaco e al cervello ci si riferisce qui, rispettivamente, alla magnetocardiografia (MCG) e alla magnetoencefalografia (MEG), o neuromagnetismo. Quest'ultima, insieme ad altre tecniche di indagine funzionale del cervello, quali la tomografia a emissione di positroni (PET, Positron emission tomography) e la risonanza magnetica funzionale (fMRI, Functional magnetic resonance imaging), consente di ottenere preziose informazioni sull'attività fisiologica delle differenti funzioni del cervello sotto esame e di monitorarne l'evoluzione temporale con elevata precisione. Si tratta di una tecnica assolutamente non invasiva, non comportando l'applicazione di campi magnetici o l'esposizione a radiazione, né il ricorso a sostanze nocive. L'intensità del campo magnetico misurato in prossimità del cranio, dovuto all'attività neuronale della regione occipitale (attività alfa, la più intensa del cervello), è di circa 100 milioni di volte più piccola del campo magnetico terrestre. Ciò comporta, nell'impiego di tali tecniche, notevoli problemi dovuti alla necessità di schermaggio e contenimento del rumore elettronico.
Analisi non distruttive sui materiali
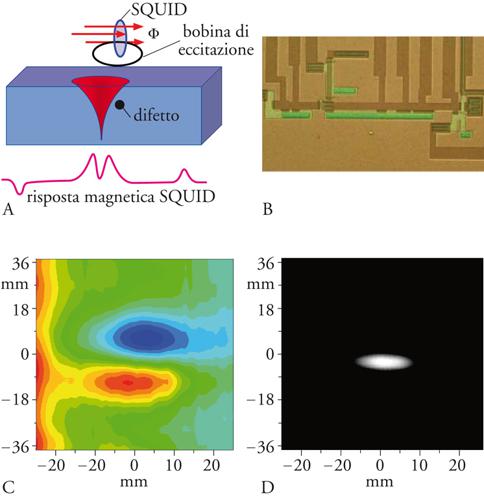
Un'altra applicazione degli SQUID riguarda le analisi non distruttive sui materiali, dove gli SQUID vengono utilizzati nella misurazione del campo magnetico prodotto dalle correnti parassite (eddy currents), indotte mediante opportune bobine sul campione in esame (fig. 4). La presenza di difetti nel materiale, quali cricche da fatica o disomogeneità causate dai processi di fabbricazione, procura un'alterazione della distribuzione delle correnti indotte e del relativo campo magnetico a esse associato. Questa tecnica è stata recentemente applicata sui materiali di interesse aerospaziale e nello studio delle caratteristiche fisiche dei materiali compositi funzionali.
Le analisi non distruttive sui materiali mediante magnetometria SQUID consentono, specialmente a basse frequenze, un'eccellente sensibilità nella rivelazione di difetti presenti in leghe metalliche anche a profondità di decine di millimetri. L'impiego di sensori SQUID basati sui superconduttori ad alta temperatura critica permette prestazioni superiori a quelle ottenibili con dispositivi convenzionali, quali bobine a induzione, sonde di Hall, flux-gate, tecniche a ultrasuoni. Ne è un esempio la rivelazione di difetti su scala millimetrica a elevata profondità in campioni di materiali compositi CFRP (Carbon fibre reinforced plastic). Nelle figg. 4C e D è riportata l'immagine di un difetto causato da un impatto con energia di 5 J. In tali compositi è stato dimostrato che è possibile rivelare danneggiamenti provocati da impatti impressi con energia inferiore a 2 J.
Cenni sulla criogenia associata
Il funzionamento dei dispositivi superconduttori richiede l'utilizzo di tecniche di criogenia associata, necessarie per poter lavorare a basse temperature. È quindi evidente che la necessità di raffreddare i dispositivi possa considerarsi come un limite per la diffusione della tecnologia superconduttiva. Naturalmente, questa è una difficoltà significativa più per applicazioni distribuite, quali possibili cavi per il trasporto di energia, che non per una dispositivistica elettronica. Nel caso degli LTS SQUID, il raffreddamento si ottiene con l'impiego di elio liquido (4,2 K), mentre per gli HTS SQUID si utilizza l'azoto liquido (77 K). La complessità dell'apparato criogenico e gli alti costi dell'elio liquido, 20 volte quello dell'azoto, hanno dato un forte impulso allo sviluppo di criogeneratori a circuito chiuso di piccole dimensioni, facilmente trasportabili e in grado di ottenere le temperature di funzionamento dei dispositivi con elevata efficienza, basso consumo energetico e stabilità in temperatura.
Bibliografia
Barone 1992: Principles and applications of superconducting quantum interference devices, edited by Antonio Barone, Singapore-London, World Scientific, 1992.
Barone, Paternò 1982: Barone Antonio - Paternò, Gianfranco, Physics and applications of the Josephson effect, New York, Wiley, 1982.
Claeson, Delsing 2001: Condensation and coherence in condensed matter, edited by Tord Claeson, Per Delsing, Stockholm, Royal Swedish Academy of Sciences, 2001.
Clarke 1994: Clarke, John, SQUIDs, "Scientific American", 271, 1994, pp. 36-44.
Clarke, Braginsky 2004-2005: Clarke, John - Braginsky, Alex I., The SQUID handbook, Weinheim, Wiley-VCH, 2004-2005.
De Gennes 1966: De Gennes, Pierre-Gilles, Superconductivity of metals and alloys, New York, Benjamin, 1966.
Kagan, Leggett 1992: Quantum tunneling in condensed media, edited by Yu Kagan, Anthony J. Leggett, Amsterdam-London, North-Holland, 1992.