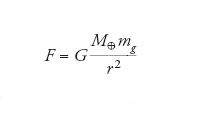Gravitazione
Gravitazione
La teoria della relatività generale (RG), di Einstein costituisce la più importante teoria della gravitazione dopo quella newtoniana, sebbene il suo pieno riconoscimento e i suoi più compiuti sviluppi siano abbastanza recenti. Infatti, tra la metà degli anni Venti e la fine degli anni Cinquanta del XX sec., si diffonde la convinzione che la RG abbia a che fare più con la matematica che con la fisica. La situazione cambia drasticamente a partire dagli anni Sessanta, quando nuove scoperte astronomiche e nuovi esperimenti riaccendono l'interesse per la RG. Questa nuova fase inizia nel 1960, con la prima conferma sperimentale dello spostamento gravitazionale della frequenza della luce, e termina nel 1979 con l'osservazione della diminuzione del periodo orbitale di una pulsar binaria di una quantità coerente con la previsione della RG della perdita di energia per emissione di onde gravitazionali. Tutti i risultati di questo periodo confermano la validità della RG e permettono di attuare una selezione nell'insieme delle teorie alternative della gravitazione che in quegli anni erano state presentate anche nella speranza di unificare RG e meccanica quantistica.
A partire dal 1980, si è dovuto prendere atto che l'indagine sperimentale e teorica sulla gravitazione nell'ambito del Sistema solare (campi gravitazionali deboli) ha raggiunto i limiti di precisione consentiti dalle tecnologie disponibili: le predizioni della RG e delle teorie antagoniste che rimangono da indagare in questo ambito sono perlopiù estremamente piccole in termini quantitativi e quindi difficili da misurare. L'investigazione delle previsioni della RG in campi gravitazionali deboli si è pertanto via via spostata verso una ricerca più opportunistica, che utilizza verifiche della gravitazione provenienti da nuove idee teoriche e moderne tecniche sperimentali. Basti pensare ai test accuratissimi della relatività ristretta che utilizzano atomi raffreddati con la tecnica del raffreddamento laser, alle proposte di una quinta forza che si risolvono in una verifica con precisione sempre maggiore del principio di equivalenza debole e, infine, alle teorie che prevedono ulteriori dimensioni, aggiuntive alle quattro dello spazio-tempo fisico, che sono alla base di recenti esperimenti per verificare l'andamento della forza di gravità a distanze minori di 100 μm.
Tuttavia, dal 1980, i maggiori sforzi si sono concentrati su esperimenti che riguardano effetti di campi gravitazionali intensi. Il parametro ε, che permette di distinguere tra campi intensi e campi deboli, è dell'ordine di GM/(Rc2), essendo G la costante gravitazionale di Newton, M la scala di massa caratteristica del fenomeno, R la scala di distanza propria del sistema in esame e c la velocità della luce nel vuoto. Vicino all'orizzonte degli eventi di un buco nero (non rotante), ε vale circa 0,5 e per una stella a neutroni circa 0,2, entrambi valori tipici del regime di gravità forte, mentre nel Sistema solare è ε〈10−5, valore tipico del regime di gravità debole. La ricerca mirante all'osservazione delle onde gravitazionali è diretta proprio a investigare regimi di gravità forte associati con la formazione e la dinamica di oggetti quali i buchi neri.
I fondamenti delle teorie della gravitazione
Il principio di equivalenza è alla base sia della teoria della gravitazione universale di Newton sia della RG di Einstein. Eppure soltanto dopo gli anni Sessanta, grazie soprattutto ai contributi di Robert H. Dicke, si è arrivati a una comprensione più profonda di questo principio come fondamento non solamente della RG ma di una più ampia classe di teorie della gravitazione basate sull'idea di uno spazio-tempo curvo. Consideriamo allora il principio di equivalenza nelle sue varie formulazioni, analizzandone le implicazioni teoriche e le prove sperimentali.
Il principio di equivalenza debole e le sue verifiche sperimentali
Il principio di equivalenza debole (PED) asserisce l'uguaglianza, a parte una costante di proporzionalità K, della massa inerziale mi e della massa gravitazionale mg di un qualunque corpo. La massa inerziale mi di un corpo si misura applicando a esso una forza nota F e stabilendo la sua accelerazione a dalla legge di Newton F=mia; quindi, mi misura l'inerzia del corpo, che si può anche interpretare come la riluttanza di un corpo a essere messo in movimento. D'altra parte, la massa gravitazionale mg è dedotta dalla legge di gravitazione di Newton. La forza di attrazione fra due corpi, per esempio, tra la Terra, di massa M⊕, e una pietra, di massa mg, vale:
[1] formula
dove G è nota come costante di gravitazione universale ed è uguale a 6,670×10−11 N∙m2∙kg−2 (ossia G/c2=7,421×10−28 m/kg, dove c è la velocità della luce nel vuoto) e r è la distanza fra i centri di massa dei due corpi.
Empiricamente, e con grande precisione, risulta mi=Kmg. Poiché K è una costante universale, possiamo ridefinire G in modo tale da avere K=1. Ne consegue che l'accelerazione di gravità g sulla Terra, espressa da GM⊕/R2⊕, con R⊕ raggio della Terra, supposta sferica, è indipendente dalla massa mg della pietra; pertanto, qualora si potesse trascurare la viscosità dell'aria, i gravi cadrebbero tutti con la stessa accelerazione. Questo fatto era già noto a Galileo Galilei e quindi il principio di equivalenza debole è anche chiamato principio di equivalenza di Galilei. I primi esperimenti di verifica del principio di equivalenza debole furono condotti da Galilei, Christiaan Huygens e Isaac Newton con l'utilizzazione di pendoli, raggiungendo una precisione che implica l'uguaglianza di mi e mg (cioè mi /mg=1) con un errore inferiore al millesimo. Le prime misure moderne con l'uso di bilance di torsione furono eseguite dal barone ungherese Loránd Eötvös. Tra il 1889 e il 1919, Eötvös e i suoi collaboratori stabilirono che il rapporto mi /mg è uguale a 1 con un errore relativo dell'ordine di qualche parte su un miliardo (ca. 5×10−9). Recentemente si è raggiunta la precisione di qualche parte su 10.000 miliardi (ca. 4×10−13 ).
Il principio di equivalenza di Einstein: conseguenze teoriche e verifiche sperimentali
Einstein si rese conto che il principio di equivalenza debole è un fatto empirico di estrema importanza e lo estese introducendo un principio fondamentale della fisica, che condiziona ogni futura teoria della gravitazione. Il suo punto di partenza fu l'esperimento concettuale (Gedankenexperiment) dell'ascensore (Tav. I). Esso si basa, innanzitutto, sull'assoluta validità del principio di equivalenza debole. Inoltre, le conclusioni ricavate (l'equivalenza fra osservazioni nelle fasi A e C e osservazioni nelle fasi B e D) valgono solamente entro certe approssimazioni: precisamente, le dimensioni del laboratorio devono essere sufficientemente piccole e i moti dei corpi devono essere nel regime non relativistico, cioè in campi gravitazionali deboli, a basse velocità e accelerazioni, assumendo la validità della meccanica newtoniana. Il risultato rivela tuttavia una straordinaria equivalenza fra inerzia e gravità, anche se questa equivalenza è valida a livello puramente locale, non potendosi espandere indefinitamente le pareti del laboratorio.
Albert Einstein trasformò questo risultato in un grande manifesto scientifico, postulandone la validità ben al di là delle assunzioni iniziali. Egli richiese, per un campo gravitazionale qualsiasi, che i sistemi di riferimento locali in caduta libera (fase C) fossero equivalenti ai sistemi di riferimento inerziali in regioni limitate dello spazio-tempo (fase A). Entro questi sistemi, le leggi della fisica verificabili con misurazioni che non implichino la gravitazione si presentano uguali a quelle della relatività ristretta. Per esempio, una misurazione della forza elettrica tra due corpi carichi è un esperimento locale non gravitazionale, mentre non lo è la misurazione della forza di attrazione gravitazionale tra due corpi. Riassumendo, il principio di equivalenza di Einstein (PEE) è l'insieme di queste tre asserzioni: (a) vale il principio di equivalenza debole; (b) il risultato di qualunque esperimento non gravitazionale è indipendente dalla velocità del sistema di riferimento locale in caduta libera nel quale esso è eseguito (invarianza locale di Lorentz); (c) il risultato di qualunque esperimento non gravitazionale è indipendente da dove e quando esso è eseguito nell'Universo (invarianza locale di posizione nello spazio-tempo). Il principio di equivalenza di Einstein è spesso chiamato anche principio di equivalenza forte, ma in anni recenti quest'ultima espressione ha assunto un significato diverso.
Negli ultimi quaranta anni gli sviluppi teorici e sperimentali relativi alla gravitazione hanno permesso di cogliere la centralità del principio di equivalenza di Einstein nell'ambito non soltanto della RG ma anche di molte teorie alternative della gravitazione. Se il principio di equivalenza di Einstein è valido, allora è possibile dedurne in modo convincente che la gravitazione è un fenomeno dello spazio-tempo curvo o, in altri termini, che gli effetti della gravitazione sono dovuti alla curvatura dello spazio-tempo. Questa conclusione è vera non soltanto per la RG ma anche per una classe di teorie, note come teorie metriche, delle quali la RG è solamente un caso particolare. Tra le teorie metriche alternative alla RG la più famosa è quella di Jordan-Fierz-Brans-Dicke, oggi comunemente nota come teoria di Brans-Dicke. Le teorie metriche soddisfano i seguenti tre postulati: (a) lo spazio-tempo è dotato di una metrica (simmetrica o, più precisamente, lo spazio-tempo è una varietà di Lorentz); (b) le traiettorie dei corpi in caduta libera sono geodetiche di quella metrica (nei sistemi di riferimento locale in caduta libera, i corpi di prova appaiono non accelerati, si muovono cioè in linea retta; tuttavia tali traiettorie localmente rettilinee corrispondono alle geodetiche in uno spazio-tempo curvo); (c) nei sistemi di riferimento locali in caduta libera, le leggi non gravitazionali della fisica sono quelle scritte nel linguaggio della relatività ristretta.
Aggiungiamo un commento al postulato (b). Il principio di equivalenza fissa, in modo quasi inequivocabile, il moto di particelle puntiformi all'interno di un campo gravitazionale, determinando il moto lungo linee, le geodetiche, che in uno spazio curvo generalizzano il concetto di linea retta. Una geodetica su una superficie è la linea più breve fra due punti ed è anche quella che più si avvicina a una retta; un esempio ci è dato dalle circonferenze massimali di una sfera. È quindi naturale richiedere che nello spazio-tempo i corpi si muovano lungo una geodetica. Così facendo, vediamo che il moto geodetico è estremamente vicino a quello newtoniano: è necessario, quindi, applicarsi molto per trovarne la differenza. A volte si rimane sconcertati dalla considerazione che, dopotutto, nello spazio ordinario la strada più breve fra la posizione attuale della Terra e quella che occuperà fra sei mesi passi direttamente attraverso il Sole, e ci si domanda come mai invece la Terra segua una perfetta orbita ellittica. Tuttavia, l'ellisse è soltanto la proiezione sullo spazio ordinario di una curva dello spazio-tempo, simile a un'elica molto allungata lungo la direzione del tempo; essendo una geodetica, essa è poi, per definizione, più diritta di qualsiasi altra linea. Quindi, l'idea di geodetica deve essere applicata a una rappresentazione quadridimensionale dello spazio-tempo e non al solo spazio ordinario tridimensionale.
Torniamo ora alle teorie metriche. Per definizione, ogni teoria metrica della gravità ha la stessa struttura spazio-temporale (varietà lorentziana) e formalmente le stesse equazioni geodetiche, ossia le medesime equazioni di moto delle particelle di prova della RG. Si può così affermare che la geometria dello spazio-tempo vincola la massa-energia a muoversi come previsto dalla teoria di Einstein; tuttavia, le equazioni di campo e la risultante metrica dello spazio-tempo definite dalle altre teorie metriche sono diverse da quelle di Einstein; quindi, la massa-energia induce sulla geometria dello spazio-tempo una curvatura in modo diverso da quanto formulato dalla RG. Vale forse la pena di soffermarsi su quest'ultimo aspetto, cercando di capire in che cosa la RG differisca dalle altre teorie metriche. Le equazioni di campo di Einstein determinano la curvatura (ovvero la metrica dello spazio-tempo) generata da una data distribuzione di massa-energia: una volta nota la metrica dello spazio-tempo, il principio di equivalenza di Einstein ci suggerisce quale sia la risposta della massa-energia alla curvatura spazio temporale. La curvatura è individuata da un campo metrico tensoriale che assegna a ogni punto dello spazio-tempo dieci numeri (le componenti del tensore metrico). Nello spazio-tempo esistono tuttavia altri tipi di campi oltre quello tensoriale della RG, tra i quali i vettoriali (che assegnano a ogni punto dello spazio-tempo quattro componenti) e gli scalari (che assegnano a ogni punto dello spazio-tempo una sola componente). Nel caso particolare delle teorie scalare-tensore, come la teoria di Brans-Dicke, al campo tensoriale metrico ne è aggiunto uno scalare: le equazioni di campo devono quindi determinare la quantità di campo scalare generata dalla materia-energia e specificare come cambia la curvatura in relazione alla materia-energia combinata con il campo scalare.
Altre teorie metriche introducono vari tipi di campi addizionali a quello tensoriale metrico; tuttavia, per ognuna di esse, una volta determinata la metrica, il principio di equivalenza di Einstein vincola la risposta della massa-energia alla curvatura spazio-temporale. Quindi, ciò che distingue una teoria metrica dall'altra è il modo in cui la massa-energia e gli eventuali campi aggiuntivi generano la metrica. Per analizzare i risultati sperimentali sulla gravitazione e paragonarli con le previsioni delle diverse teorie metriche, Kenneth Nordtvedt ha sviluppato negli anni Sessanta una tecnica, introdotta da Arthur S. Eddington negli anni Venti, che va sotto il nome di formalismo PPN (Parametrised post-newtonian formalism). Alla base di questo approccio sta la constatazione che, nel limite di campo gravitazionale debole e di moti con velocità piccola rispetto a quella della luce, è relativamente semplice confrontare tra loro le diverse teorie metriche e mettere in relazione le loro previsioni con i risultati sperimentali. Entro questo limite, noto come limite post-newtoniano, perché prende in considerazione soltanto la prima correzione introdotta dalle nuove teorie a quella della gravitazione di Newton, l'approssimazione ottenuta ha un'accuratezza sufficiente per la trattazione della maggioranza dei test sperimentali della gravitazione, sia terrestri sia spaziali, condotti nell'ambito del Sistema solare. Risulta inoltre che, entro lo stesso limite, la metrica dello spazio-tempo delle diverse teorie della gravitazione ha una struttura generale basata sul valore di un comune insieme di parametri: diversi valori dell'insieme di parametri individuano differenti teorie metriche.
I parametri rilevanti nel caso di teorie metriche che ammettano la conservazione dell'energia-impulso sono essenzialmente cinque: γ, che misura la curvatura prodotta dalla massa-energia in relazione alla curvatura della RG; β, che misura la non linearità rispetto alla RG; ξ, che misura la dipendenza degli effetti gravitazionali dalla posizione; α1 e α2, che misurano la dipendenza degli effetti gravitazionali dalla velocità. Per la RG si ha γ=1, β=1, ξ=α1=α2=0, mentre per la teoria di Brans-Dicke si ha γ=(1+ω)/(2+ω), β=1, ξ=α1=α2=0, dove la costante ω, il cui valore viene corretto in funzione dei dati sperimentali, misura la rilevanza del campo scalare nella determinazione della curvatura: più grande è il suo valore, minore è l'influenza del campo scalare, fino al limite di ω→∞ nel quale la teoria di Brans-Dicke diventa identica alla RG.
Non tutte le teorie della gravitazione elaborate negli ultimi decenni sono teorie metriche nel senso sopra esposto. Per esempio, le cosiddette teorie di superstringa, che ugualmente si basano su una metrica spazio temporale anche se trattano oggetti che vivono in spazi di dimensione superiore a quella dello spazio-tempo quadridimensionale, richiedono l'introduzione di campi addizionali (dilatoni, moduli) che si accoppiano alla materia-energia in modo tale da portare a una violazione del principio di equivalenza di Einstein (in particolare, del principio di equivalenza debole).
Per quanto riguarda la verifica sperimentale dei vari asserti del principio di equivalenza di Einstein, abbiamo già parlato della prima delle tre asserzioni, che esprime la validità del principio di equivalenza debole. La seconda asserzione, cioè l'invarianza locale di Lorentz, può considerarsi di fatto verificata in tutti gli esperimenti che confermino le previsioni della relatività ristretta, come avviene di frequente in quelli di fisica delle alte energie; non è però facile, anche a causa dei complicati effetti legati alla presenza delle interazioni forti e deboli, interpretarli quali prove dell'invarianza locale di Lorentz. L'esperimento, che molti autori giudicano come la verifica diretta dell'invarianza locale di Lorentz, riguarda una misura dell'anisotropia nella massa inerziale ed è stato condotto per la prima volta da Vernon Hughes (1960) e da Ron Drever (1961).
Se le propietà inerziali di un corpo dipendessero dalla distribuzione delle masse nell'Universo, si potrebbe pensare per esempio che la massa inerziale di un corpo in caduta libera verso il centro della Galassia (dove è concentrata una massa maggiore) sia diversa da quella dello stesso corpo in caduta libera in direzione perpendicolare alla precedente. L'esperimento di Hughes e Drever stabilisce l'isotropia a meno di una parte su 1027.
La terza asserzione del principio di equivalenza di Einstein è l'invarianza locale di posizione, che può essere provata misurando lo spostamento verso il rosso (redshift) della luce che risale un campo gravitazionale. Einstein, già nel 1907, aveva concepito il redshift gravitazionale della luce come un esperimento a supporto della nuova teoria della gravitazione (formulata compiutamente solo nel 1916). Oggi il redshift è visto più in generale come un fenomeno a favore del principio di equivalenza di Einstein, che quindi non discrimina tra la RG e le altre teorie metriche.
Sulla base del principio di equivalenza debole, del principio di conservazione dell'energia e di alcuni principî base di meccanica classica e quantistica, possiamo derivare un'espressione del redshift in approssimazione di campo debole utilizzando il seguente Gedankenexperiment. Si costruisca una macchina per il moto perpetuo, con un tubo piegato a formare un anello e posto verticalmente. Il tubo è pieno di un fluido di atomi aventi due stati, uno fondamentale e uno eccitato, separati da un'energia E=hν, con h costante di Planck e ν frequenza del fotone emesso dall'atomo nel passaggio dallo stato eccitato a quello fondamentale o assorbito nel passaggio inverso. La macchina è posta su un astro che ha accelerazione di gravità aG. Il fluido ascende lungo il ramo destro e discende lungo quello sinistro. Entrambi i rami hanno altezza l. Gli atomi in ascesa sono nello stato fondamentale e quelli in discesa nello stato eccitato. Una volta arrivati in basso, gli atomi eccitati emettono un fotone che viene spedito verso l'alto per essere quindi riassorbito dagli atomi dello stato fondamentale in ascesa. Poiché la massa di un atomo eccitato è maggiore di quella dell'atomo nello stato fondamentale, il fluido discendente è più pesante di quello ascendente e si ottiene un guadagno energetico di EaGl/c2.
Sappiamo però che, per il principio di conservazione dell'energia, il moto perpetuo non è possibile. Tuttavia la macchina funziona solamente se il fotone emesso e quello assorbito hanno la stessa energia. Evitiamo quindi il paradosso se assumiamo che il fotone, in ascesa nel campo gravitazionale, perda esattamente l'energia che si spera di ottenere dall'atomo durante un ciclo. Questo implica che la frequenza ν del fotone emesso da un atomo debba diminuire, salendo dal ramo orizzontale basso a quello alto, della frazione ΔV/c2, dove ΔV=aGl è la variazione di potenziale gravitazionale nel passaggio dal primo al secondo ramo. Precisamente, si ha Δν=νaGl/c2, da cui hΔν=hνaGl/c2=EaGl/c2: la perdita di energia per fotone pareggia così il guadagno energetico della macchina, in accordo con il principio di conservazione dell'energia. Nel risalire un campo gravitazionale il fotone perde quindi energia, cioè la sua frequenza diminuisce (nello spettro del visibile si sposta verso la regione del rosso). Per converso, un fotone che scende lungo il campo gravitazionale aumenta la sua energia, e quindi la sua frequenza (nello spettro del visibile si sposta verso la regione del blu, blueshift). A entrambi i fenomeni, redshift e blueshift, si attribuisce comunque il nome di redshift gravitazionale. La diminuzione della frequenza di un fotone che esce dalla Terra e viene osservato da distanza infinita, ossia fuori dal campo gravitazionale, è dell'ordine di GM⊕/(c2r⊕), che equivale a circa una parte su un miliardo.
Usando raggi gamma emessi dal Fe57, Robert V. Pound e Glen A. Rebka (1960) e lo stesso Pound e Joseph L. Snider (1965) hanno misurato per la prima volta con grande precisione (errore relativo di circa l'1%) il redshift gravitazionale, trovandolo pari a Δν/ν≃−2,46×10−15 su una salita di soli 22,6 m, in perfetto accordo con le previsioni teoriche. Ulteriori esperimenti sono stati condotti in seguito; uno dei più accurati è stato realizzato alla fine degli anni Settanta con due orologi atomici, uno a terra e uno su un razzo lanciato a un'altezza di circa 10.000 km, confermando le previsioni teoriche con un errore dell'ordine di 1 su 10.000. Lo spostamento verso il rosso gravitazionale è stato osservato in un certo numero di corpi celesti. Nel Sole ammonta a due parti su un milione ed è difficile, ma non impossibile, vederlo a causa dell'allargamento termico delle linee dello spettro. L'effetto è molto più evidente per le nane bianche e dovrebbe avvicinarsi al 10% su una stella di neutroni. Il redshift gravitazionale, per quanto detto, potrebbe simulare l'effetto Doppler dovuto alla recessione della sorgente, e qualcuno l'ha anche proposto in alternativa all'effetto Doppler cosmologico (interpretato come espansione dell'Universo) per spiegare il redshift osservato nella luce emessa dalle galassie. Questa interpretazione non ha però avuto molto successo: un corpo il cui campo gravitazionale dovesse produrre un redshift di un fattore 2 o anche maggiore (come quelli osservati per le galassie) sarebbe infatti pericolosamente vicino al collasso gravitazionale e la sua configurazione sarebbe estremamente instabile. Ricapitolando, il principio di equivalenza di Einstein ha ricevuto conferme sperimentali sempre più accurate. Tuttavia, gli attuali sviluppi della fisica teorica sembrano prevedere una violazione del PEE a qualche livello, dovuta a effetti di gravità quantistica derivanti dalle teorie di stringa o a interazioni ancora non conosciute. Ecco perché si continuano a progettare nuovi esperimenti come STEP (Satellite test of the equivalence principle), attuato da una collaborazione NASA-ESA-CNES, che ha l'obiettivo di verificare l'equivalenza tra massa inerziale e gravitazionale con un errore dell'ordine o minore di 1 su 1017.
Teorie della gravitazione a confronto: gli esperimenti classici della relatività generale
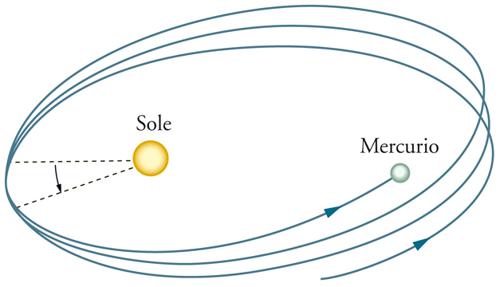
Quando si parla di esperimenti classici della RG ci si riferisce solitamente alla precessione del perielio di Mercurio, alla deflessione della luce e al redshift gravitazionale, cioè ai tre effetti che per primi sono stati considerati negli scritti di Einstein. Tuttavia, come già osservato, il redshift gravitazionale non è più oggi considerato un test della RG, ma un test del principio di equivalenza di Einstein comune a tutte le teorie metriche. Un confronto tra la RG e le altre teorie metriche può quindi essere realizzato facendo riferimento agli altri due esperimenti classici e alle loro conseguenze. Usando il formalismo PPN, i risultati di questi esperimenti nell'ambito del Sistema solare possono essere interpretati come misure per la stima dei valori dei vari parametri e la conseguente determinazione di quale sia la teoria che meglio si adatta alle osservazioni. Il perielio di Mercurio compie una precessione (fig. 3) di circa 5600″ a secolo, tutti, salvo 43″, spiegati dalla perturbazione newtoniana dovuta agli altri pianeti. Calcolando esattamente il moto dei pianeti con le equazioni della RG, si dimostra che si può dar conto dei 43″ addizionali e predire effetti simili per gli altri pianeti, anch'essi in accordo con le osservazioni. Questo accordo tra previsioni teoriche e dati sperimentali è molto importante, poiché dipende da caratteristiche proprie della RG che non hanno precedenti nella teoria newtoniana.
Sfortunatamente, l'interpretazione dell'avanzamento del perielio di Mercurio come chiara conferma della teoria della RG è complicata: errori sistematici di osservazione ed errori nella valutazione degli effetti planetari potrebbero invalidare l'accordo. Sull'avanzamento del perielio di Mercurio possono influire numerosi fattori. Tra questi, uno dei più indagati è quello relativo allo schiacciamento polare del Sole, che porterebbe all'introduzione di un contributo del termine di quadrupolo J2 nel potenziale gravitazionale. Se si assume che il Sole ruoti su sé stesso con una velocità angolare uniforme che produce lo schiacciamento polare, misurando la velocità di rotazione del Sole è possibile dedurre un valore sufficientemente piccolo, J2≈10−7, che giustifichi il pieno accordo tra la RG e la precessione del perielio di Mercurio. Una serie di misure ottenute nel 1966 da Dicke e H. Mark Goldenberg dà invece J2≈2,5×10−5, un valore che implica un disaccordo tra RG nella sua formulazione standard e dati osservati sulla precessione di Mercurio. Anche su questa base sono state approfondite le ricerche di teorie della gravità, competitive con la RG, tra le quali, in particolare, la teoria di Brans-Dicke. In questa gli effetti, come la precessione del perielio di Mercurio, sono spiegati in modo diverso che nella RG standard: sono messi in relazione allo schiacciamento polare del Sole e fatti dipendere dal campo scalare aggiuntivo introdotto nella teoria. Se il valore di J2 fosse dell'ordine di quello trovato da Dicke e Goldenberg, esso contribuirebbe a spiegare 4″ dei 43″ dell'avanzamento del perielio di Mercurio, ponendo seri limiti all'accordo tra previsioni della RG e osservazioni, mentre la teoria di Brans-Dicke sarebbe in perfetto accordo fissando uguale a circa 5 la costante ω che compare nel parametro γ del formalismo PPN.
Altre osservazioni sul Sistema solare, delle quali parleremo tra breve, forniscono invece valori di ω ben più alti. D'altra parte, a partire dal 1982, ulteriori misurazioni, anche se non ancora definitive, hanno portato a un valore del termine di quadrupolo tra 10−6 e 10−7, assai prossimo a quello richiesto per il pieno accordo tra precessione di Mercurio e teoria della RG nella sua formulazione standard, permettendo al contempo di elevare il valore di ω come richiesto da altre evidenze sperimentali. Si può comunque affermare che la precessione di Mercurio rimane uno dei capisaldi osservativi della teoria della RG, anche perché pone limiti stringenti su teorie competitive come quella di Brans-Dicke. Accanto alla precessione del perielio di Mercurio sono state recentemente migliorate le misure relative alle precessioni di altri pianeti. Il perielio di Venere compie una precessione di circa 5069″ a secolo, dei quali solamente 8,6″ necessitano delle correzioni della RG; per la Terra si hanno 6189″, dei quali soltanto 4″ richiedono correzioni della RG; per Marte si hanno 6627″, dei quali soltanto 1,35″ necessitano delle correzioni della RG. A causa della minore entità degli effetti non spiegabili nell'ambito della teoria newtoniana, queste misurazioni risultano più difficili di quelle relative al perielio di Mercurio.
Parlando di precessioni delle orbite vale la pena di citare le pulsar binarie. La prima pulsar binaria, PSR 1913+16, è stata scoperta nel 1974 da Russel Hulse e Joseph Taylor; a questa, a partire dagli anni Novanta, si è via via aggiunta un'intera famiglia di pulsar binarie. Esse costituiscono un laboratorio naturale unico per verificare gli effetti relativistici. PSR 1913+16 è composta da due corpi collassati, probabilmente ambedue stelle a neutroni, con un raggio di circa 10 km, con un'orbita molto stretta ed eccentrica con semiasse maggiore di circa 700.000 km ‒ giusto per dare un'idea, l'orbita del sistema binario potrebbe essere contenuta all'interno del Sole ‒ e un periodo di rivoluzione di circa 8 ore. Uno soltanto dei due corpi emette pulsazioni con un periodo di 59 ms; l'altro (detto stella compagna) potrebbe essere anche una nana bianca, una stella di elio o un buco nero. In queste condizioni, la precessione del periastro è di 4,22° ad anno ed è abbastanza facile da osservare. Riparleremo delle pulsar binarie nell'ambito degli effetti legati ai campi gravitazionali intensi. Va ricordato, comunque, che ancora oggi la RG è la teoria che fornisce le migliori e più dirette previsioni per quanto concerne l'avanzamento del periastro nelle pulsar binarie.
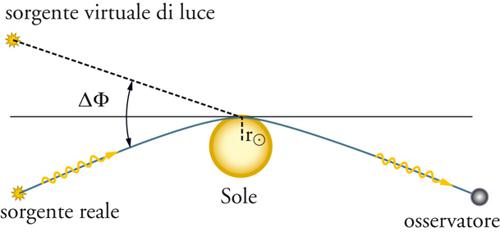
Il secondo test classico riguarda la deflessione della luce. Einstein divenne famoso nel mondo dopo l'esatta predizione della deflessione Δφ (fig. 4) dei raggi di luce che passano radenti al bordo del Sole (cioè a una distanza pari al raggio R⊙ del Sole; per distanze d>R⊙ la deflessione diminuisce ed è uguale a circa 1,75″ R⊙/d). In una delle prime versioni della teoria (1911), Einstein predisse un valore (0,87″ di arco) che è in realtà solamente la metà di quello corretto (circa 1,75″ di arco, come comunicato dallo stesso Einstein nel novembre del 1915). Vari ostacoli, tra i quali l'inizio della Prima guerra mondiale, impedirono un esperimento prematuro che avrebbe screditato la teoria. Nel 1919, la spedizione di Eddington a Prince Island, nell'emisfero meridionale, riuscì finalmente a compiere osservazioni su un'eclissi totale di Sole che concordavano con il valore teorico corretto. Utilizzando il formalismo PPN, la deflessione per raggi radenti al Sole è espressa da [(1+γ)/2]1,75″. Il coefficiente (1+γ)/2, che ha valore 1 nella RG, assume valori differenti nelle diverse teorie metriche a seconda del valore assunto da γ: il primo addendo, 1/2, può essere calcolato ricorrendo soltanto al principio di equivalenza, determinando la deflessione che si produce in una sequenza di osservatori in caduta libera lungo la traiettoria del fotone nel passaggio da un osservatore all'altro; il secondo addendo, γ/2, dipende dal fatto che a causa della curvatura dello spazio-tempo le linee rette locali sono curvate proprio da questo fattore relativamente alle linee rette lontane (asintoticamente) dal Sole.
Se l'approssimazione delle prime misure di deflessione della luce condotte da Eddington era di circa il 30%, gli sviluppi della radioastronomia hanno notevolmente aumentato l'accuratezza delle misure, in buon accordo con la RG. Recenti esperimenti che utilizzano un radiotelescopio per osservare vari gruppi di quasar periodicamente nascosti dal Sole, hanno errori relativi che vanno da qualche parte su 1000, (1+γ)/2=0,9996±0,0017, a qualche parte su 10.000, (1+γ)/2=0,99992±0,00014, in buon accordo con le previsioni della RG.
La deflessione gravitazionale è presente ogni qualvolta ci siano masse interposte tra la sorgente e il ricevitore. Einstein, già nel 1936, aveva considerato alcune sorprendenti conseguenze astronomiche di questo effetto. Supponendo la presenza di un corpo di massa molto grande interposto tra la Terra e un oggetto astronomico distante (come una quasar), Einstein aveva previsto che la luce passando su bordi opposti del corpo fosse deviata verso l'esterno simulando due immagini dello stesso oggetto. Nel 1979 è stata osservata effettivamente per la prima volta una coppia di quasar, separate nel cielo di soli 6″, che mostravano identiche componenti dello spettro di emissione con spostamenti verso il rosso assolutamente uguali. Successivamente, tra il 1980 e il 1981, ricerche ottiche hanno evidenziato la presenza di una debole galassia ellittica collegata a un ammasso di galassie, a distanza di 1″ da una delle immagini. È la prima evidenza che una galassia, o un ammasso di galassie, che si frappone tra noi e una quasar si comporta come una gigantesca lente gravitazionale. L'effetto finale è quello di simulare la presenza di due o più quasar con la stessa distribuzione spettrale e lo stesso redshift gravitazionale; inoltre, eventuali fluttuazioni di luminosità di un'immagine si ripresentano nell'altra, con un ritardo di alcuni mesi dovuto alla differenza di cammino ottico. Dal numero e dalle caratteristiche delle immagini prodotte da tali lenti gravitazionali si sono potute ricavare preziose informazioni sulle loro dimensioni e distanze. Per queste ragioni queste 'lenti galattiche' sono sfruttate per diminuire le incertezze sul valore della costante di Hubble, un dato di primaria importanza nello sviluppo dei modelli cosmologici.
Strettamente legato alla deflessione della luce è un altro test di alta precisione sulla curvatura dello spazio-tempo noto come ritardo temporale di Shapiro, dal nome dello scienziato Irwin Shapiro che lo propose nel 1964. Esso riguarda il ritardo dei segnali di luce che passano vicino al Sole ed è alla base di esperimenti assai accurati che utilizzano, in particolare, la propagazione di onde radio. Nel vuoto queste si propagano alla velocità costante della luce; quindi la misurazione del tempo di andata e ritorno di un segnale inviato dalla Terra su un pianeta permette di ricavare la distanza tra il pianeta e la Terra. Nel caso di Marte, la cui orbita è particolarmente eccentrica, questa distanza varia da un valore minimo di circa 80 milioni di km a un valore massimo di circa 380 milioni di km, tranne quando il cammino delle onde Terra-Marte passa vicino al bordo del Sole. In quella regione Marte sembra muoversi fuori dalla sua orbita, allontanandosi progressivamente fino a circa 30 km (equivalenti a un ritardo anomalo di circa 200 μs) prima di tornare nuovamente al suo cammino normale: per circa due mesi e mezzo Marte appare spostato di più di 15 km dalla sua orbita. La spiegazione di tale fenomeno è che per effetto della massa solare la luce viaggia più lentamente nelle vicinanze del Sole.
Nell'espressione del ritardo temporale in condizioni di campo debole compare di nuovo il fattore (1+γ)/2, indicazione dello stretto legame tra questo fenomeno e la deflessione della luce. Gli attuali risultati, ottenuti da Shapiro per il ritardo temporale e per la deflessione della luce con la tecnica VLBI (Very-long-baseline radio interferometry), che riesce ad apprezzare differenze angolari dell'ordine di 100 microarcosecondi, danno (1+γ)/2=1, a meno di circa 2 parti su 10.000. Quest'ultimo risultato porta a fissare per le teorie metriche con scalare e tensore del tipo Brans-Dicke un valore ω>3500.
Il principio di equivalenza forte
Il principio di equivalenza di Einstein asserisce che l'invarianza locale di Lorentz e l'invarianza locale di posizione sono rispettate da tutte le leggi della fisica che non coinvolgano la gravitazione. Se si estende il principio di equivalenza di Einstein, localmente, a tutte le leggi della fisica compresa la gravitazione, si ha il cosiddetto principio di equivalenza forte (PEF), secondo il quale non solamente i corpi di prova (quelli di dimensione degli usuali laboratori) ma anche i corpi celesti (pianeti e stelle) cadono tutti con la stessa accelerazione in un campo gravitazionale esterno. Inoltre, in analogia con la seconda e terza asserzione del principio di equivalenza di Einstein, in un sistema di riferimento locale in caduta libera abbastanza grande da contenere corpi come pianeti o stelle, tutte le leggi della fisica, comprese quelle della gravitazione, non dipendono né dalla velocità né dalla posizione spazio-temporale del sistema di riferimento in caduta libera.
Il PEF è un principio molto più vincolante di quello di equivalenza di Einstein e, a tutt'oggi, l'unica teoria metrica che non lo violi è la RG. Per questo, gli esperimenti di verifica del principio di equivalenza forte acquistano una particolare importanza tra gli esperimenti di conferma della RG. Una violazione del PEF implicherebbe che l'energia di legame gravitazionale di un corpo contribuisca in modo diverso alla massa inerziale e alla massa gravitazionale del corpo stesso. Questo fatto, considerato per la prima volta da Nordtvedt nel 1968 e da allora noto come effetto Nordtvedt, può essere messo in evidenza da osservazioni sulle orbite di rivoluzione del sistema Terra-Luna in una sorta di esperimento planetario di tipo Eötvös. A causa, infatti, delle differenze tra massa inerziale e massa gravitazionale, la Terra e la Luna dovrebbero palesare differenti accelerazioni di caduta sul Sole, che si tradurrebbero in una elongazione dell'orbita lunare nella direzione Terra-Sole. A partire dalla missione Apollo del 1969 sono stati sistemati sulla Luna opportuni riflettori di raggi laser inviati dalla Terra. Il LURE (Lunar laser ranging experiment) utilizza proprio questo sistema di riflettori, misurando i tempi di andata e ritorno dei segnali luminosi e ricavando precise misure della distanza Terra-Luna.
I dati accumulati in circa trent'anni di osservazioni sistematiche permettono oggi di conoscere la distanza Terra-Luna nelle varie fasi dell'orbita lunare con un'accuratezza che ha raggiunto il centimetro (equivalente a circa 50 ps). La precisione raggiunta implica che l'identità tra massa inerziale e massa gravitazionale per la Terra e la Luna è verificata a meno di 5 parti su 1013. I risultati dell'esperimento, inoltre, implicano che nella teoria di Brans-Dicke la costante di accoppiamento ω debba essere maggiore di 1000. Tra le conseguenze del PEF ne va segnalata un'altra di grande interesse sia teorico sia sperimentale. L'invarianza locale di posizione spazio-temporale contenuta nel principio di equivalenza di Einstein, di cui abbiamo già detto, ha un'importante implicazione: tutte le costanti fisiche fondamentali (come la velocità della luce nel vuoto, la costante di Planck, la carica e la massa dell'elettrone, la massa del protone, ecc.) che compaiono nelle leggi fisiche non gravitazionali devono essere indipendenti dal tempo. Se il principio di equivalenza forte è valido, allora anche le costanti che compaiono nelle leggi di gravitazione, in particolare la costante G di gravitazione, devono essere indipendenti dal tempo.
Varie teorie contemplano violazioni del PEF. Gli esempi più noti di teorie che contemplano la variazione di G con il tempo sono la cosmologia ipotizzata da Paul Dirac tra il 1937 e il 1938 e le teorie metriche con scalare e tensore, come la teoria di Brans-Dicke. Secondo l'idea di Ernest Mach, la massa inerziale mi e la massa gravitazionale mg di un corpo dipendono dalla distribuzione delle altre masse nell'Universo. Quello che di fatto possiamo misurare direttamente non è mg, ma Gmg. Si può allora ipotizzare che G muta al variare della distribuzione e del moto della massa-energia nell'Universo, per esempio a causa dell'espansione di quest'ultimo. Nella teoria di Brans-Dicke G effettivamente dipende da una funzione, determinata dalla distribuzione di massa-energia dell'Universo, identificata con il campo scalare aggiuntivo. La questione è uno dei punti più interessanti dell'attuale dibattito sulla gravitazione, anche alla luce di nuove evidenze sperimentali. Attualmente gli esperimenti più accurati per determinare la dipendenza di G dal tempo indicano un limite di variazione di G su scala di tempo cosmico inferiore a qualche parte su 1011 anni.
Campi gravitazionali intensi e onde gravitazionali
Nel Sistema solare il campo gravitazionale è sufficientemente debole da poter applicare il formalismo PPN, utilizzando soltanto il primo termine di correzione alla teoria newtoniana. La questione è più complessa nel caso di campi gravitazionali intensi, evidenziati da molte situazioni astronomiche. Quelle oggi maggiormente studiate sono relative alla formazione, struttura e dinamica delle stelle di neutroni e dei buchi neri. In alcuni casi è possibile tentare di calcolare correzioni di ordine superiore del formalismo PPN; in altri, le tecniche di analisi da utilizzare sono diverse; tra esse si segnalano le ricerche di una soluzione generale delle equazioni di Einstein con metodi numerici, uno dei settori attualmente in espansione. D'altra parte, nell'ambito dei campi gravitazionali intensi le teorie della gravitazione e delle particelle elementari (in particolare la teoria quantistica dei campi, nota come Modello Standard delle particelle e le teorie di stringa) hanno una forte intersezione che complica ulteriormente il quadro.
Proprio come il campo di Maxwell possiede 'quanti' (i fotoni) associati alla propagazione di onde, si suppone che anche il campo gravitazionale abbia 'quanti' (i gravitoni) associati a moti ondulatori. Le equazioni di campo per la gravitazione sono non lineari e ciò rende difficile determinare soluzioni esatte per onde gravitazionali arbitrarie. Se ci limitiamo al caso più realistico delle onde deboli, è allora possibile risolvere l'equazione di campo della RG con il metodo della approssimazione lineare; questa è certamente adeguata per la maggior parte degli scopi. Le onde gravitazionali si propagano alla velocità della luce e, proprio come la luce, hanno due distinti stati di polarizzazione. Tuttavia i gravitoni sono particelle di spin 2 e il loro comportamento, se sottoposti a una rotazione, è abbastanza diverso da quello dei fotoni (particelle di spin 1). Infatti, se si ruota il campo lungo la linea di propagazione, il gravitone torna nella posizione originale dopo 180°; per i fotoni ciò accade dopo 360°, per gli elettroni (particelle di spin 1/2) dopo 720°: in generale, servono 360°/J, dove J è lo spin della particella. Ulteriori differenze si verificano anche nel meccanismo di emissione di radiazione e possono essere viste nel seguente modo. È noto che una particella carica accelerata perde energia per emissione di radiazione; in prima approssimazione, la potenza emessa è analoga a quella di un dipolo elettrico oscillante ed è direttamente proporzionale alla quarta potenza della frequenza ν della radiazione. La formula corrispondente per l'emissione gravitazionale da parte di una massa accelerata fornisce invece una potenza dell'ordine di ν6, perché nel caso gravitazionale si ha a che fare con un'emissione di quadrupolo. Non esiste, infatti, nessuna radiazione di dipolo per le onde gravitazionali (questo è vero nella RG ma non in altre teorie alternative della gravitazione) e, naturalmente, nessuna radiazione di monopolo, come avviene anche nel campo di Maxwell. Da ciò consegue che si producono onde gravitazionali solamente per particolari moti accelerati delle masse, del tipo di quelli nei quali la sorgente cambia forma, cioè nei casi in cui la dinamica non è uguale in tutte le direzioni (dinamica non sferica). Vibrazioni o collassi di stelle puramente sferici non producono radiazione gravitazionale.
Oltre a quelle appena ricordate, esiste un'altra fondamentale differenza tra onde elettromagnetiche e onde gravitazionali, che ha importanti conseguenze sul piano sperimentale: la potenza emessa da masse accelerate è sempre estremamente piccola, e quindi di difficile osservazione, a differenza di quella emessa da corpi carichi accelerati (che per questo è utilizzata in innumerevoli dispositivi di uso quotidiano, come, per es., le antenne di trasmissione e ricezione di segnali per le radiocomunicazioni).
La potenza emessa da masse accelerate diventa una frazione apprezzabile se la massa M vibra o compie moti di rivoluzione a velocità relativistiche ad altissima frequenza. Condizioni che, seppure lontanamente, richiamano questa situazione sono veramente rare. Alcuni dei fenomeni candidati per l'emissione di radiazione gravitazionale potenzialmente osservabile sono: il collasso di una supernova non isotropa (una stella che esplode e il cui nucleo collassa in modo disuguale nelle diverse direzioni); la collisione tra due stelle di neutroni; il moto a spirale di due buchi neri che cadono l'uno sull'altro fino a unirsi. Quanto lontane siano queste situazioni da quelle che si presentano nel Sistema solare è dimostrato dal calcolo applicato al caso del moto di rivoluzione della Terra, dal quale si ricava che la perdita di energia per emissione di onde gravitazionali ha il valore irrisorio di 200 W circa, ossia l'energia dissipata da una comune lampadina alogena. Ciò significa che un collasso gravitazionale dell'orbita terrestre avverrebbe fra circa 1024 anni. Altre cause, quali perturbazioni da parte dei pianeti, probabilmente agiranno molto prima, diciamo fra circa 1010 anni. Nel caso della pulsar binaria PSR 1913+16, di cui abbiamo già parlato, il periodo di rivoluzione è di poche ore e il sistema dovrebbe decadere fra circa 109 anni. Questo fa sì che la perdita di energia per emissione di onde gravitazionali abbia un valore entro i limiti di osservazione: la perdita di energia si evidenzia nella diminuzione del periodo orbitale di 7,2×10−5 secondi all'anno circa. Si è potuto così concludere che l'effetto esiste in perfetto accordo con la teoria dell'approssimazione di quadrupolo.
Tuttavia, siamo di fronte in questo caso a evidenze indirette delle onde gravitazionali; vediamo le perdite di energia del sistema che le emette ma non siamo in grado di riceverle nel nostro laboratorio. Proprio per ottenere questo risultato, molti gruppi di ricercatori, sulla spinta del lavoro pionieristico di Joseph Weber (iniziato nei primi anni Sessanta nell'Università del Maryland a Baltimora), hanno cominciato a costruire ricevitori gravitazionali (antenne gravitazionali). Generalmente, questi dispositivi sono grandi cilindri di alluminio. Le onde in entrata (che ci si aspetta nella regione di 1 kHz) produrranno piccole oscillazioni nella forma del cilindro che, se tutto procede correttamente, potranno essere rilevate. La sensibilità degli apparati di misura di onde gravitazionali può essere espressa dal rapporto Δl/l tra l'ampiezza Δl dell'oscillazione prodotta nell'antenna e la lunghezza l dell'antenna. Nel caso dei primi strumenti utilizzati da Weber, questa sensibilità non era superiore a 10−15. Negli anni successivi, raffreddando il cilindro (per diminuire gli effetti dovuti all'agitazione termica) e utilizzando cavità con materiale superconduttore, questo tipo di strumenti ha raggiunto sensibilità dell'ordine di 10−18, che significa grosso modo riuscire ad apprezzare una vibrazione delle estremità della barra dell'ordine del centomilionesimo delle dimensioni di un atomo di idrogeno su una lunghezza di qualche metro. Solo con una grande dose di fortuna si può pensare di osservare un tale evento.
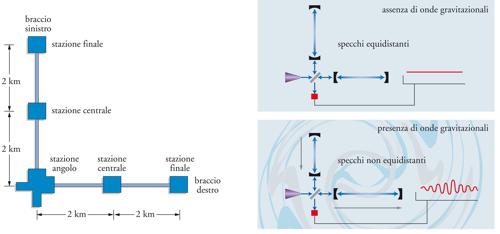
Sono stati anche progettati ricevitori gravitazionali basati su schemi interferometrici, la cui sensibilità sarebbe molto più elevata (10−22 e oltre). Essi sono costituiti da due gallerie lunghe alcuni chilometri che si intersecano ad angolo retto. Alle estremità delle gallerie e nel punto di intersezione sono sospese masse le cui distanze relative sono misurate accuratamente per mezzo di impulsi laser. In tal modo è possibile apprezzare cambiamenti della distanza tra le masse dell'ordine di un centomilionesimo del diametro di un atomo di idrogeno (su distanze di vari chilometri). I rivelatori LIGO (Laser interferometer gravitational-wave observatory), costruiti negli Stati Uniti da una collaborazione tra Caltech e MIT) (fig. 6) e VIRGO, realizzato in Italia da una cooperazione tra enti di ricerca francesi e italiani, nonché GEO600 (nato da una collaborazione tra Germania e Inghilterra) e TAMA300 (Giappone), sono già quasi tutti operativi. A questi si aggiungerà, intorno al 2015, LISA (Laser interferometer space antenna), nato da una cooperazione ESA-NASA, un interferometro laser orbitante costituito da tre navicelle spaziali separate da distanze di milioni di chilometri. La rilevazione diretta di onde gravitazionali aprirebbe nuove strade all'astrofisica, permettendo di seguire in dettaglio i collassi gravitazionali di supernovae e molti altri fenomeni che coinvolgono stelle di neutroni e buchi neri. Non è escluso, inoltre, che si arrivi a rilevare onde gravitazionali provenienti da altre galassie. Si spera, così, di dare inizio alla cosiddetta astronomia gravitazionale.
Bibliografia
Dyson 1979: Dyson, Freeman J., Disturbing the Universe, New York-London, Harper and Row, 1979 (trad. it.: Turbare l'universo, Torino, Bollati Boringhieri, 1981).
Dyson 1988: Dyson, Freeman J., Infinite in all directions, New York-London, Harper and Row, 1988 (trad. it.: Infinito in ogni direzione, Milano, Rizzoli, 1989).
Hawking 1988: Hawking, Stephen W., A brief history of time: from big bang to black holes, Boston (Mass.), G.K. Hall, 1988 (trad. it.: Dal big bang ai buchi neri, Milano, Rizzoli, 1988).
Livio 2003: Livio, Mario, La bellezza imperfetta del cosmo, Torino, UTET, 2003.
Regge 1995: Regge, Tullio, Infinito. Viaggio ai limiti dell'universo, Milano, Mondadori, 1995.
Regge 1999: Regge, Tullio, L'universo senza fine. Breve storia del Tutto: passato e futuro del cosmo, Milano, Mondadori, 1999.
Regge, Peruzzi 2003: Regge, Tullio - Peruzzi, Giulio, Spazio, tempo e universo. Passato, presente e futuro della teoria della relatività, Torino, UTET, 2003.
Schwinger 1986: Schwinger, Julian, Einstein's legacy, New York, Freeman, 1986 (trad. it.: L'eredità di Einstein. L'unità di spazio e tempo, Bologna, Zanichelli, 1988).
Wald 1977: Wald, Robert M., Space time and gravity: the theory of the big bang and black holes, Chicago-London, University of Chicago Press, 1977 (trad. it.: Teoria del big bang e buchi neri, Torino, Bollati Boringhieri, 1980).
Weinberg 1977: Weinberg, Steven, The first three minutes, Glasgow, Collins, 1977 (trad. it.: I primi tre minuti, Milano, Mondadori, 1986).
Weinberg 1992: Weinberg, Steven, Dreams of a final theory, New York, Pantheon, 1992 (trad. it.: Il sogno dell'unità dell'universo, Milano, Mondadori, 1993).
Wheeler 1990: Wheeler, John A., A journey into gravity and spacetime, New York, Scientific American Library, 1990 (trad. it.: Gravità e spazio-tempo, Bologna, Zanichelli, 1993).
Will 1986: Will, Clifford M., Was Einstein right? Putting general relativity to the test, New York, Basic Books, 1986 (trad. it.: Einstein aveva ragione? Le prove sperimentali della relatività generale, Torino, Bollati Boringhieri, 1989).