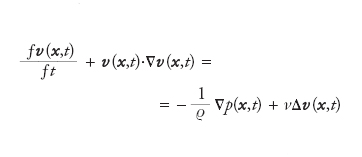numero di Reynolds
numero di Reynolds
L’evoluzione di un fluido incompressibile (cioè tale che ∇∙v(x, t)=0) è descritta dalle equazioni di Navier-Stokes
dove v(x,t) è il campo di velocità nel punto x al tempo t, p(x,t) la pressione, ϱ densità del fluido e ν la viscosità cinematica. Indicando con V e L rispettivamente la velocità e la dimensione lineare caratteristiche e fissata la geometria del sistema, l’unico parametro rilevante è il numero di Reynolds Re=VL/ν. Per convincersi di questo è sufficiente usare variabili adimensionali, cioè v′=v/V, x′=x/L, t′=tV/L, p′= p/(ϱV2) e notare che nelle equazioni di Navier-Stokes per le variabili adimensionali appare solo Re. Questo risultato è importante anche a livello tecnologico: permette, infatti, di utilizzare esperimenti su modelli a scala ridotta. Intuitivamente il numero di Reynolds indica il rapporto tra il valore tipico del termine non lineare v∙∇v, di ordine V2/L e di quello lineare ν∇v, di ordine νV/L2. Per piccoli valori di Re il campo di velocità ha un comportamento regolare (moto laminare); per valori di Re dell’ordine di 100 si osserva un moto con strutture spazialmente ben organizzate ma con un’evoluzione temporalmente caotica. La transizione da un comportamento regolare a uno caotico al variare di un parametro di controllo è un fenomeno piuttosto comune. Per es., nel moto convettivo di un fluido tra due piani orizzontali, riscaldato dal basso (convezione di Rayleigh-Bénard) il parametro è il numero di Rayleigh R=ϱ0gαL3ΔT/χν dove ΔT è la differenza di temperatura tra i due piani, ϱ0 è la densità media del fluido, g è l’accelerazione di gravità, α il coefficiente di dilatazione termica e χ il coefficiente di diffusione termica.
→ Caos deterministico; Turbolenza