omologia
omologia
omologia termine che assume diversi significati a seconda del contesto.
☐ In geometria elementare, si dicono vertici omologhi i vertici di due angoli congruenti in due triangoli simili, e lati omologhi i lati opposti ad angoli congruenti.
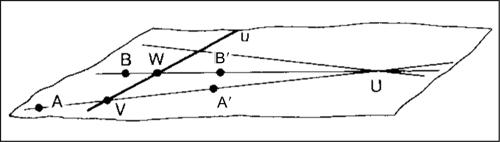
☐ In geometria proiettiva, l’omologia è una particolare → omografia, tale che ogni punto e il suo trasformato sono allineati con un punto fisso U detto centro dell’omologia. È detta anche omologia proiettiva perché è il più generale tipo di omologia. L’omologia piana (detta anche proiettività omologica) è una omografia di un piano proiettivo in sé che ha un centro e una retta u luogo di punti uniti, detta asse dell’omologia. Per dualità, nel piano esiste un fascio di rette unite il cui centro è detto centro dell’omologia. Se il centro appartiene all’asse la trasformazione è detta omologia speciale. Un’omologia piana è univocamente determinata dal centro U, dall’asse u e da una coppia qualsiasi di punti corrispondenti. Ogni coppia di punti A, A′, che sono corrispondenti e distinti, è allineata col centro. Se A, A′ e B, B′ sono due coppie di punti corrispondenti e se V e W sono le intersezioni di u rispettivamente con le rette AA′ e BB′, vale la relazione tra i birapporti (AA′VU) = (BB′WU) = k e il numero k si dice caratteristica dell’omologia. Se U è un punto improprio e u una retta propria, l’omologia prende il nome di omologia affine (o affinità omologica). Se la direzione del centro U (improprio) è perpendicolare all’asse u, l’omologia si dice omologia ortogonale, altrimenti omologia obliqua; in questo caso k si riduce al rapporto semplice (AA′V) e se risulta k = −1 l’omologia si dice simmetrica rispetto all’asse. Se viceversa U è un punto proprio e u la retta impropria, l’omologia è una → omotetia; in particolare, se risulta k = −1, è una → simmetria centrale di centro U. Se asse e centro dell’omologia sono entrambi impropri si ha una → traslazione (per gli aspetti grafico-costruttivi si vedano → affinità omologica e → proiettività omologica). L’omologia spaziale è analoga a quella piana: in essa esiste una stella di piani uniti il cui centro S è il centro dell’omologia e, per dualità, un piano σ di punti uniti che costituisce il piano dell’omologia. La caratteristica dell’omologia è il valore costante k che assume il birapporto (SRPP′ ), avendo indicato con P e P′ due qualsiasi punti corrispondenti e con R l’intersezione del piano σ con la retta PP′. Se risulta k = −1 l’omologia si dice omologia armonica.
☐ In topologia algebrica, il termine «omologia» indica un metodo per assegnare degli invarianti a uno spazio topologico. È utilizzato correntemente al posto di «gruppi di omologia» così come si usa dire «omologia di dimensione i» anziché «i-esimo gruppo di omologia» (→ omologia, gruppi di). La teoria dell’omologia ha come oggetto la specificazione di alcune proprietà geometriche e di caratteri topologici di una varietà mediante un opportuno gruppo abeliano, detto gruppo di omologia della varietà, che ne costituisce un invariante topologico. Per la determinazione dei gruppi di omologia delle varietà si può ricorrere a diversi procedimenti, come la triangolazione, che consiste nel sostituire una varietà con opportuni complessi simpliciali, per l’analisi dei quali esistono algoritmi appropriati studiati nell’ambito della topologia combinatoria. La teoria dell’omologia presenta vari sviluppi, alcuni dei quali, con carattere prevalentemente algebrico, riguardano l’omologia come esempio notevole di funtore, mentre altri, con carattere prevalentemente geometrico, stabiliscono legami con la teoria dell’omotopia.