poliedro
poliedro
La forma di un mattone, di un dado, di un cristallo
Un libro, i mattoni per muratura, ma anche i dadi per giocare o un pallone da calcio sono oggetti dalle forme geometriche semplici, regolari, che l’uomo ha realizzato per i più diversi scopi. Ma anche in natura, nel regno delle cose non viventi, esistono oggetti con forme regolari stupefacenti per la loro perfezione, come se qualcuno le avesse scolpite
Progettare poliedri
Molti oggetti realizzati dall’uomo hanno forme regolari. Per esempio, un mattone è un parallelepipedo rettangolo (perché ha sei facce rettangolari) tutte disposte ad angolo retto fra loro.
Ci sono motivi precisi per scegliere tali forme regolari: posti l’uno sopra l’altro, i mattoni permettono di costruire solidi muri verticali senza che tra essi rimangano spazi vuoti. Il parallelepipedo è un esempio di poliedro, forse il più diffuso, perché dà la forma a scatole, libri, stanze e così via.
Un poliedro è una figura solida delimitata da facce a forma di poligono. I lati delle facce sono gli spigoli del poliedro e i punti comuni agli spigoli costituiscono i vertici.
Poliedri regolari
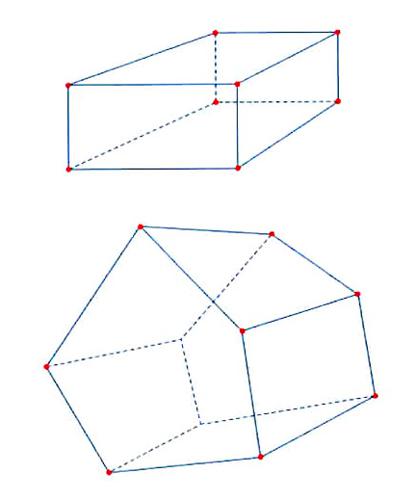
Se tutte le facce sono poligoni regolari dello stesso tipo e di uguali misure, il poliedro si dice regolare. Un parallelepipedo rettangolo (la forma tipica di un mattone) e l’altro poliedro qui raffigurati (v. fig.)non sono regolari. Un esempio di poliedro regolare è invece il cubo perché le sue facce sono costituite da sei quadrati uguali.
I dadi da gioco sono a forma di cubo. La regolarità del cubo è importante, perché ne garantisce la simmetria. Essendo tutte uguali e tutte ugualmente disposte rispetto al centro del cubo, non esistono facce ‘privilegiate’, ma tutte hanno la stessa probabilità di ‘uscire’ dopo il lancio. I poliedri regolari sono quelli più interessanti; sono infatti simmetrici rispetto al loro centro e, inoltre, hanno una particolarità che destò stupore fin dall’antichità: ne esistono soltanto cinque diversi tipi.
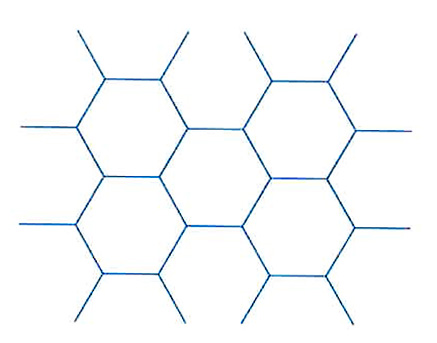
Per capire il motivo si può partire da un poliedro non regolare, molto noto perché dà la struttura a uno dei modelli più diffusi di pallone da calcio. Questo pallone è formato da 20 esagoni e 10 pentagoni. Ma perché non sono stati usati solo esagoni? La spiegazione è semplice: gli esagoni non permettono di fare ‘piegature’ lungo i lati e con essi si può ottenere solo una superficie piana (v. fig.), come pavimento piatto senza poter dare quella curvatura che serve per formare una sfera.
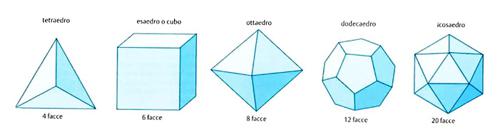
Gli angoli dell’esagono, infatti, misurano ciascuno 120° e, disponendo vicini tre esagoni, gli angoli, sommati, formano un angolo di 360°, cioè un intero angolo giro. Per questo motivo non esiste nessun poliedro regolare che abbia facce con 6 o più lati e gli unici casi possibili sono quelli con facce di 3, 4 o 5 lati. I poliedri regolari possibili sono soltanto quelli raffigurati in fondo alla pagina (v. fig.).
Regolarità dell’uomo e della natura
Il filosofo greco Platone era convinto che l’essenza del mondo fosse di tipo matematico e attribuiva la forma dei poliedri regolari agli elementi che formavano (secondo le convinzioni dell’epoca) la materia: il tetraedro per il fuoco, l’ottaedro per l’aria, l’icosaedro per l’acqua, il cubo per la terra. All’ultimo poliedro regolare, il dodecaedro, spettava un ruolo particolare: «C’era tuttavia una quinta combinazione», scrive Platone nel dialogo intitolato Timeo, «e Dio l’usò per decorare l’universo». Per tale motivo i poliedri regolari sono ancora oggi chiamati solidi platonici.
Torniamo ora agli oggetti progettati e costruiti dall’uomo. Può non sorprendere che abbiano forme regolari con facce lisce e angoli uguali, invece è stupefacente che anche in natura si trovino forme così regolari da sembrare scolpite intenzionalmente. Il legame particolarmente forte che unisce gli atomi di alcune sostanze – dette cristalli – fa sì che, in condizioni opportune, esse crescano riproducendo su grande scala le regolarità del reticolo atomico e quindi abbiano forme poliedriche quasi perfette.