Rendita

Rendita

Premessa

La rendita è stata inizialmente considerata come quel surplus che va al proprietario terriero per l'uso produttivo della terra scarsa. Successivamente e con ripetuti ampliamenti la rendita è stata definita, nei termini più generali possibili, come un surplus dovuto a differenze o tra costi di produzione di una stessa merce, essendo il saggio di profitto uniforme, o tra redditi per l'uso di un fattore produttivo impiegato nella produzione di una stessa merce in diverse condizioni di produzione, o tra prezzi pagati e pagabili per uno stesso bene. Queste definizioni individuano due categorie di rendita: quella astrattamente generale e di natura classificatoria; quella connessa specificamente alla distribuzione del reddito e alla dinamica con scarsità.

Sotto il profilo astrattamente generale-classificatorio la rendita viene definita in almeno tre modi: 1) come la differenza positiva (X-Y) tra il pagamento che un fattore di produzione riceve (X) e quello che esso riceverebbe nell'impiego successivo in termini di redditività (Y); 2) come il reddito che un fattore di produzione riceve (Z) al netto (Z-z) di quello minimo occorrente per mantenere il fattore stesso in attività (z) in quanto un pagamento inferiore a z porterebbe il proprietario del fattore a non impiegarlo più; 3) come la differenza (C-c) tra il costo di produzione di una merce prodotta nelle condizioni peggiori (C) e quello nelle condizioni migliori (c), ovviamente essendo C maggiore di c e andando la rendita a chi produce nelle condizioni migliori.

La seconda categoria di rendita si connette alle tipologie di scarsità di certi mezzi di produzione, innanzitutto a quelle delle risorse naturali e della terra (ma non esclusivamente); in questo caso essa emerge quale perdurante grandezza nella crescita economica e nella distribuzione del reddito a fianco di salari e profitti. Noi seguiremo questa linea d'analisi ripercorrendone l'evoluzione storico-analitica, che presuppone entro certi limiti la conoscenza dei problemi della distribuzione del reddito e della ricchezza, della crescita, della dinamica.

I classici

Il punto di partenza è rappresentato dai classici e in particolare da Adam Smith, Thomas Robert Malthus e soprattutto David Ricardo, per il quale "la rendita è quella parte del prodotto della terra che viene pagata al proprietario per l'uso dei poteri originari e indistruttibili del suolo" (v. Ricardo, 1817; tr. it., p. 222). Impossibile ripercorrere le analisi della rendita di tutti questi autori data l'ampiezza. Ci concentreremo su Ricardo, comunemente reputato come il teorico più completo al proposito, con cenni brevissimi agli altri due.

Merito di Adam Smith è probabilmente l'individuazione della rendita della terra e delle miniere come surplus (v. Smith, 1776, libro I, cap. 11). In Smith ci sono tuttavia varie concezioni della rendita (tra le quali quella di prezzo di monopolio pagato per l'uso della terra e quella di rendita di posizione) che comunque non sono centrali nella sua teoria (v. Schumpeter, 1954; tr. it., vol. I, cap. 5), per la quale la ricchezza delle nazioni dipende dall'abilità e dalla divisione del lavoro nella manifattura, sicché la scarsità delle terre, da cui dipende la rendita, non ha un ruolo capace di arrestare i processi di crescita. Da ciò discende anche una visione ottimistica sulle possibilità di crescita.

Thomas Robert Malthus (v., 1798 e 1814) esprime invece una visione pessimistica affermando che tra popolazione e produzione alimentare esiste un divario strutturale, in quanto la prima cresce in progressione geometrica mentre la seconda cresce in progressione aritmetica. Le risorse naturali agricole sono caratterizzate da scarsità assoluta e la rendita surplus va dunque a tutte le terre indipendentemente dalle loro diverse fertilità.

In generale per i classici (tra cui anche James Anderson ed Edward West) la rendita è un surplus sul costo di produzione sulla terra agricola, incluso il reddito dell'agricoltore. La dimensione del surplus dipende dalla domanda dei prodotti agricoli e dai costi dell'offerta, che a loro volta dipendono dalla fertilità e dalla localizzazione della terra. I beneficiari di questo surplus sono i proprietari terrieri.

David Ricardo: rendita surplus e scarsità dinamica

La formulazione rigorosa del concetto di rendita surplus è data da Ricardo, che l'anticipa nello Essay (1815) e la elabora nei Principles (1817). Nella Prefazione ai Principles egli dice che, senza la conoscenza della dottrina della rendita, non è possibile capire l'effetto del progresso della ricchezza sui profitti e sui salari. Tre sono le proposizioni fondamentali di Ricardo.

1. Rendita, distribuzione e accumulazione. - "Nei diversi stadi della società le proporzioni di tutto il prodotto della terra assegnate a ognuna di queste classi [proprietari della terra, proprietari del capitale, lavoratori] sotto il nome di rendita, profitto e salari saranno essenzialmente diverse; soprattutto a seconda dell'effettiva fertilità del suolo, dell'accumulazione del capitale e della popolazione, e a seconda dell'abilità, ingegnosità e strumenti impiegati nell'agricoltura" (v. Ricardo, 1817; tr. it., p. 165).

2. Rendita, produttività e dinamica. - "È [...] perché la quantità della terra non è illimitata e la sua qualità non è uniforme, e perché man mano che la popolazione aumenta viene coltivata terra di qualità inferiore o in posizione meno vantaggiosa, che si paga una rendita per il suo uso. Quando, col progredire della società, viene coltivata una terra di secondo grado di fertilità, si forma subito una rendita su quella di prima qualità, il cui ammontare dipenderà dalla differenza di qualità di queste due porzioni di terra" (pp. 224 s.)."Ogni successivo aumento della popolazione, costringendo un paese a ricorrere a terra di qualità inferiore per poter incrementare la sua provvista di alimenti, aumenterà la rendita su tutte le terre più fertili" (pp. 225 s.)."Tutto ciò che diminuisce la differenza nel prodotto ottenuto da successive proporzioni di capitale impiegato sulla terra o su una terra nuova tende ad abbassare la rendita; e tutto ciò che aumenta questa differenza produce necessariamente un effetto opposto e tende ad aumentarla" (pp. 236 s.).

3. Rendita e prezzi. - "La ragione per cui il valore relativo del prodotto grezzo aumenta è perché per produrre l'ultima porzione ottenuta viene impiegata una maggiore quantità di lavoro e non perché si paga una rendita al proprietario. Il valore del grano è regolato dalla quantità di lavoro impiegato per produrlo su quella qualità di terra o con quella parte di capitale che non paga rendita. Il grano non è caro perché si paga una rendita, ma si paga una rendita perché il grano è caro" (p. 229)."La materia prima entra nella composizione di gran parte delle merci ma il valore di quelle materie prime, come quello del grano, è determinato dalla produttività della porzione di capitale impiegato per ultimo sulla terra che non paga; perciò la rendita non è una parte componente del prezzo delle merci" (v. Ricardo, 1817, ed. 1951, p. 78).

4. In conclusione: la rendita deriva dai costi crescenti della produzione agricola quando la produzione cresce. La proprietà tecnica della decrescente fertilità della terra (rendimenti decrescenti estensivi che causano la rendita estensiva) e la proprietà per cui aumenti nel lavoro e nel capitale applicato alla stessa terra generano decrescenti aumenti di produzione (rendimenti decrescenti intensivi che generano la rendita intensiva) stanno alla base sia delle leggi dei rendimenti decrescenti sia dei due tipi di rendita, estensiva e intensiva.

Il costo dell'ultima unità prodotta che, a causa dei rendimenti decrescenti, è più alto di quello di tutte le precedenti, determina a sua volta il prezzo del grano. È questo differenziale di costi che configura la rendita come surplus a vantaggio delle terre e dei processi (e dei proprietari) ove si produce a costi più bassi, essendo il saggio di profitto uniforme per la concorrenza e il salario unitario, anch'esso uniforme, alle sussistenze. Perciò la rendita è una conseguenza e non la causa dell'alto prezzo del grano e non entra nella teoria del valore. Un aumento della domanda, che aumenta il prezzo ma non cambia la produzione, non aumenta la rendita ma il profitto. La rendita non influenza i prezzi ma la distribuzione del prodotto netto e il profitto di cui è antagonista.

A noi sembra che il disegno di Ricardo si sia posto come intermedio, a proposito di dinamica con risorse naturali, tra il pessimismo malthusiano (scarsità assoluta) e l'ottimismo smithiano (producibilità assoluta) incorporando il principio della scarsità relativa, in quanto le diverse terre esistenti non configurano una scarsità assoluta finché c'è crescita, che è sostenuta anche dal progresso tecnico. Ricardo, sottovalutando il progresso tecnico, prevede però in conclusione la caduta del saggio di profitto, l'arresto dell'accumulazione e lo stato stazionario con scarsità assoluta. In tale situazione estrema la rendita diventa massima. In agricoltura l'aumento del costo di produzione per unità di prodotto comprime il saggio di profitto essendo dato il salario. La conseguente crescita del prezzo del grano porta con sé l'aumento dei salari monetari che in tal modo, a fronte della crescita dei prezzi, mantengono stabili i salari reali, i quali altrimenti andrebbero sotto il livello delle sussistenze. Ma l'aumento dei salari monetari determina la caduta del profitto in tutti i settori dell'economia e quindi l'arresto dell'accumulazione (v. Pasinetti, 1960).

I marginalisti: rendita marginalistica e scarsità statica

La teoria marginalistica o neoclassica della distribuzione del reddito e della rendita ebbe il suo periodo fondativo tra il 1871 e il 1936. Tra i molti, due sembrano essere i più chiari e importanti autori per l'analisi della rendita: Wicksteed e Marshall, gli unici tra l'altro citati a questo proposito dal 'neoricardiano' Sraffa.

Wicksteed: la produttività marginale e la rendita

Philip H. Wicksteed, definito da Sraffa il "purista della teoria marginale" (v. Sraffa, 1960, p. VI), presenta la teoria della distribuzione del reddito basata sulla produttività marginale come 'evoluzione' della teoria ricardiana della rendita intensiva e dei rendimenti decrescenti intensivi in base all'ipotesi di sostituibilità continua tra fattori di produzione, di concorrenza perfetta e di particolari funzioni di produzione (v. Wicksteed, 1894).

La scarsità statica e generale dei fattori (terra, lavoro, capitale) li pone tutti su di uno stesso piano per un impiego efficiente in base alle loro produttività marginali, che a loro volta ne determinano la remunerazione. Di nuovo si impone una citazione integrale, data la sua nitidezza.

"Nello studio delle leggi della distribuzione si è considerato di solito ciascuno dei grandi fattori di produzione, quali la Terra, il Capitale e il Lavoro, separatamente, ricercando le condizioni speciali in cui il fattore partecipa alla produzione, [... e] deducendo da tutti questi elementi una legge particolare che regola la quota di prodotto spettante a quel fattore all'atto della distribuzione [...]. Fintantoché la legge della rendita, ad esempio, si basa su uno standard oggettivo di fertilità della terra, mentre la legge dell'interesse si fonda su uno standard soggettivo di valutazione del futuro rispetto al presente, risulta difficile persino poter concepire un qualsiasi calcolo per cui la quota della terra e la quota del capitale vengano sommate, per poi verificare se la quota residua coincida o meno con quella che la teoria assegna ai salari. [...] La base comune a queste leggi non deve essere cercata nella speciale natura dei servizi resi dai vari fattori ma nel fatto, a tutti comune, di prestare un servizio [... misurato] nel suo impiego marginale" (v. Wicksteed, 1894; tr. it., pp. 126 s.).

Dunque: la legge della produttività marginale della terra determina la rendita. La stessa legge applicata a ogni altro fattore garantisce, laddove sia applicabile il teorema di Eulero, l'esaurimento del prodotto. È inutile, anzi sbagliato, considerare la rendita come surplus, essendo possibile dimostrare che, date certe condizioni, la rendita surplus coincide con quella individuabile in base alla produttività marginale.

Marshall: generalizzazioni su rendita e quasi-rendita

L'altro studioso considerato neoclassico, ma con una teoria della rendita di ben più ampia generalità, è Alfred Marshall che nei suoi Principles (1890) da un lato cerca di mantenere la continuità con l'impostazione classica, dall'altro contribuisce alla nuova concezione marginalistica della distribuzione e apporta specifici contributi allo studio della rendita. Sono tre le proposizioni marshalliane da citare.La prima è la definizione della rendita come un caso particolare del più generale caso del surplus del produttore: "La rendita della terra non è un caso unico ma semplicemente la specie principale di un largo genere di fenomeni economici; [...] la teoria della rendita della terra [... è] una delle principali applicazioni di un corollario derivato dalla teoria generale della domanda e dell'offerta; [...] vi è una graduazione continua che va dalla vera rendita di quei doni naturali di cui si è appropriato l'uomo ai redditi derivati dai miglioramenti permanenti del suolo, a quelli generati da costruzioni rurali e industriali, da macchine a vapore e beni meno durevoli. [...] il reddito netto della terra [... è diviso] in due parti. Una parte si riferisce alla quantità totale del reddito netto, o surplus del produttore, dalla terra; l'altra al modo con cui questo reddito è distribuito tra quelli che hanno un interesse nella terra" (v. Marshall, 1890, ed. 1920⁸, p. 523).

La seconda è la definizione di quasi-rendita: "Ciò che è giustamente considerato come interesse sul capitale 'libero' o 'fluttuante', o su nuovi investimenti di capitale, va trattato più propriamente come un tipo di rendita - una quasi-rendita [...] - sui vecchi investimenti di capitale. E non vi è una rigida linea di demarcazione tra il capitale libero e quello che è stato 'immobilizzato' per uno specifico ramo di produzione, né tra nuovi e vecchi investimenti di capitale; ogni gruppo sfuma dentro l'altro gradualmente. E perciò anche la rendita della terra è vista non come una grandezza a sé stante ma come la specie principale di un genere più largo; anche se per il vero essa ha sue proprie peculiarità che sono di vitale importanza dal punto di vista sia teorico che pratico" (v. Marshall, 1890, Prefazione).

Il tempo è di importanza centrale per la distinzione tra rendita e quasi-rendita, in quanto la prima si ha se l'offerta di un fattore di produzione limitato non può essere aumentata quale che sia il periodo di tempo.

La terza è la distinzione, che Marshall considera labile, tra rendita da scarsità e rendita differenziale: "In un certo senso tutte le rendite sono rendite di scarsità e tutte le rendite sono rendite differenziali. Ma in certi casi conviene valutare la rendita di un certo fattore confrontandone il reddito con quello di un fattore inferiore (o forse marginale) quando questo sia applicato analogamente con gli opportuni strumenti. In altri casi è meglio andare sino alle relazioni fondamentali della domanda alla scarsità o abbondanza dei mezzi per la produzione di quelle merci per cui serve il fattore considerato" (v. Marshall, 1890; tr. it., p. 578).

Scarsità dinamica e statica, rendita surplus e marginalistica

Con le precedenti riflessioni non abbiamo proposto una rassegna delle analisi sulla rendita, di solito connesse a quelle sulla distribuzione del reddito (v. Cannan, 1893; v. Fetter, 1932; v. Stigler, 1941; v. Schumpeter, 1954; v. Valassina, 1976; v. Quadrio Curzio, 1987 e 1993), ma ne abbiamo individuato i concetti fondamentali.

È utile soffermarsi conclusivamente sulla differenza tra rendita-surplus e rendita-marginalistica, ovvero tra Ricardo e Wicksteed. Al proposito Sraffa (v., 1960, p. V) rileva che la rendita estensiva e i rendimenti decrescenti estensivi ricardiani vengono trascurati dai marginalisti in quanto essi non implicano cambiamenti nelle proporzioni dei fattori produttivi sulla cui base si determina il prodotto marginale e il costo marginale.

La rendita estensiva è differenziale per le diverse terre a differente fertilità. La rendita intensiva è uniforme per terre omogenee e determinabile in base alla produttività marginale. Entrambe le rendite derivano da una 'scarsità', ma di diverso tipo: quella marginalistica è statica e generale, quella ricardiana è dinamica e relativa. Marshall per certi versi sta tra Ricardo e Wicksteed. In particolare con la quasi-rendita, derivante da scarsità temporanee, si possono interpretare categorie generali per tutte le risorse scarse (naturali o non) ma anche aumentabili nel tempo sia per sostituzione che per progresso tecnico.

Verso l'abbandono della rendita

I classici e Ricardo hanno posto le basi delle teorie della scarsità e della dinamica e su queste hanno fondato la rendita. Marshall ha pure contribuito a chiarire la natura della rendita. Da allora passiamo agli anni trenta del Novecento - in questo 'intermezzo' non ci sono stati contributi centrali su questi temi -, quando prendono l'avvio varie linee di analisi che si interessano di crescita e scarsità. In particolare vi sono quella sulle scarsità specifiche delle risorse naturali, che inizia con Hotelling, e quella sulla crescita senza scarsità, che inizia con Harrod e von Neumann. Nessuno di questi filoni considera però in modo significativo la rendita.

Riferiamoci qui solo al secondo per la sua ripresa della dinamica classica, anche se è difficile definire unitariamente queste teorie come 'post-classiche', pur avendo esse in comune l'attenzione per i fenomeni dinamici della produzione e dell'accumulazione. Tra i molti, sono due i filoni principali che a noi interessano. Uno è quello macroeconomico avviato da Roy Harrod (v., 1939 e 1948); l'altro è quello multisettoriale di John von Neumann (v., 1937) che, pur con qualche differenza, sarà affiancato dal metodo delle interdipendenze industriali di Leontief (v., 1941).

Questi autori accennano alla scarsità della terra e delle risorse naturali per escluderne una rilevanza nella crescita. Più tardi J. Robinson (v., 1956) e J. Meade (v., 1961) terranno conto della terra e della rendita, ma con modalità piuttosto superate. Nel complesso tuttavia il problema è trascurato, come rivelano una importante rassegna di teoria della crescita (v. Hahn e Matthews, 1965) e questa affermazione di J. Hicks: "La crescita in equilibrio [... ha varie] difficoltà da fronteggiare che sono abbastanza serie. Una, ben nota, è la questione della terra; solo quando l'offerta di terra è abbondante, un'economia può mantenersi in equilibrio di crescita con una tecnologia invariata. Se si trascura questa obiezione, allora si sta seguendo Smith e non Ricardo; ma ritornare a uno stato di innocenza senza rendimenti decrescenti non è cosa che si possa fare sentendosi a proprio agio. Tuttavia, per ora, è quello che faremo qui" (v. Hicks, 1965, pp. 133 s.).

Sraffa: una nuova teoria della rendita con radici classico-ricardiane

È invece merito di Sraffa avere elaborato con geniale originalità una teoria multisettoriale della produzione, della distribuzione e dei prezzi, che riprende l'impostazione ricardiana sulla 'terra', sulle 'risorse naturali' e sulla 'rendita'.Sraffa con Produzione (v., 1960; tr. it., cap. XI) inserisce la scarsità delle risorse naturali in processi produttivi circolari (ma trascura la dinamica che è centrale nella rendita ricardiana) e definisce la rendita con le seguenti fondamentali proposizioni.

Risorse naturali e merci non-base. "Le risorse naturali che sono usate per la produzione, come la terra e i giacimenti minerari, e che essendo scarse permettono ai loro proprietari di ottenere una rendita, si può dire che occupino tra i mezzi di produzione un posto equivalente a quello che le merci non-base hanno tra i prodotti. Essendo impiegate nella produzione senza che siano esse stesse prodotte, rappresentano l'inverso di quelle merci che, per quanto prodotte, non sono usate nella produzione" (ibid., p. 94).

Rendita estensiva. "Se si impiegano n diverse qualità di terra, esse daranno luogo a un eguale numero di diversi metodi di produzione del grano [...] vi saranno quindi n equazioni della produzione alle quali si deve aggiungere la condizione che una delle terre non dà alcuna rendita". "L'ordine di fertilità [...] non viene definito indipendentemente dalle rendite [e quindi dai prezzi]; tale ordine può variare con la variazione del saggio di profitto e del salario unitario" (pp. 94-95).

Rendita intensiva. "Se la qualità della terra è uniforme e la sua disponibilità è limitata, questo di per sé rende compatibile l'uso su terre simili di due diversi processi produttivi [...] l'uno a fianco dell'altro, determinando una rendita uniforme per ettaro". "L'esistenza di due metodi l'uno a fianco dell'altro può essere considerata come una fase nel corso di un progressivo aumento dei prodotti ottenuti dalla terra". "Mentre la scarsità di terra crea [...] la situazione da cui sorge la rendita, il solo segno visibile di tale scarsità che si riscontri nel processo di produzione è la coesistenza di due metodi su terre della stessa qualità" (pp. 96-97).

Quasi-rendita. "Macchine di modello antiquato che son tenute ancora in funzione sono paragonabili alla terra in quanto vengono usate come mezzi di produzione benché non siano più prodotte. Se ci è consentito di usare il termine marshalliano di quasi-rendita in un senso più restrittivo di quello datogli da Marshall, diremo che la quasi-rendita che viene percepita per quegli elementi di capitale fisso in uso normale nel passato ma che sono ormai superati per quanto valga la pena di impiegarli fino a consumazione, è determinata precisamente nello stesso modo della rendita della terra" (p. 99).

Valutazioni di sintesi ed estensioni. Con queste proposizioni Sraffa getta le basi della moderna teoria della rendita anche se vari problemi sono solo abbozzati. Non valuteremo criticamente la teoria di Sraffa, i cui meriti vanno ben oltre le possibili perplessità, ma ne rileviamo i limiti principali: l'accostamento tra risorse naturali e merci non-base è discutibile in quanto le risorse naturali tramite le materie prime influenzano tutte le variabili dell'economia, a meno che ci si trovi in un contesto uniperiodale senza cambiamenti nelle quantità prodotte; il problema di un 'ordine di fertilità' tra i processi con terra e dei suoi cambiamenti non viene risolto.

Più in generale Sraffa non si interessa o non porta a conclusione questi problemi: la distinzione tra fertilità delle terre ed efficienza dei processi che le utilizzano, in quanto l'efficienza dipende da tutta la tecnologia del sistema economico; la distinzione tra l'ordine di efficienza da seguire nell'attivare le terre e l'ordine delle rendite; gli effetti che le variazioni nelle quantità prodotte esercitano sulle rendite; gli effetti che le variazioni della grandezza distributiva esogena (salario per unità di lavoro o saggio di profitto) hanno sull'ordine di efficienza dei processi con terre e sulle rendite; il ruolo dell'accumulazione della dinamica e del cambiamento tecnologico con tutti i loro effetti su quantità, prezzi, distribuzione e rendite.

In definitiva vengono trascurate le relazioni tra variazioni nel sistema prezzi-distribuzione-rendite e variazioni nel sistema terre-grano-produzione, essendo il modello Sraffa a quantità fisse. Per questi motivi l'impostazione di Sraffa su risorse-scarsità-rendita, mentre da un lato è di grande originalità ed è alla base della moderna teoria della rendita, da un altro lato presenta dei limiti poi superati da vari autori, a cominciare da Quadrio Curzio con Rendita (1967) e con altri lavori (v. bibliografia) che seguiremo qui attraverso la trattazione di Quadrio Curzio e Pellizzari (v., 1996) che, dopo aver ricompreso generalizzandoli i precedenti studi, va molto oltre.

Verso una definizione più generale: la rendita tecnologica

In termini intuitivi che si ricollegano alle definizioni prima date si può dire che la rendita è il reddito che va a un fattore di produzione scarso che non ha un costo di produzione (e che non è prodotto o non è producibile, quantomeno nell'orizzonte temporale considerato, a tecniche date). Esempio tipico è la 'terra'. E poiché tale fattore serve direttamente o indirettamente alla produzione di tutte le merci dell'economia perché produce il 'grano', la determinazione del reddito della 'terra' si connette a quella di altre variabili. In altri termini, la determinazione della rendita può essere fatta solo in connessione a quella delle altre grandezze distributive (salari e profitti) e dei prezzi delle merci. Proprio per questo motivo la rendita è una categoria distributiva tutt'altro che arcaica o solo agraria.

Ma c'è di più: la 'terra' è solo uno dei mezzi di produzione non prodotti di qualità data e scarsa, e il 'grano' è solo una delle materie prime o merci prodotte con l'uso di 'terra'. Vi sono infatti altre risorse naturali come i giacimenti minerari e vi sono anche mezzi di produzione prodotti al presente o in passato che percepiscono una rendita. Si considerino al proposito due altri casi. Nel primo caso un processo produttivo utilizza una macchina innovativa che nessun altro processo relativo alla produzione dello stesso bene usa. Il costo di produzione del processo innovativo per la produzione del bene è più basso di quello degli altri processi in attività che determinano il prezzo del bene, generando una rendita per la macchina innovativa. Nel secondo caso un processo utilizza una macchina tecnicamente superata e del tutto ammortizzata che non dà più luogo a una componente di costo. Altri usano macchine innovative più efficienti, ma non ammortizzate e tali quindi da comportare una componente positiva nel costo di produzione della merce che risulta più alto di quello relativo al processo con la macchina tecnicamente superata, la quale percepisce perciò una rendita. I mezzi di produzione che generano rendita possono perciò essere la terra (che non è prodotta), le miniere (che non sono prodotte ma si esauriscono), le macchine antiquate (prodotte ma non più riprodotte), le macchine innovative (prodotte ma non diffuse a tutti i processi). Tutti questi casi presentano distinzioni che non potremo considerare qui. Ciò che importa rilevare è che la teoria della rendita da noi riferita nel seguito alla 'terra' e al 'grano', intesi qui come sinonimi di categorie ben più generali, si può applicare, con opportune modificazioni, a molti altri casi. Di qui innanzi useremo come sinonimi: 'terra' e mezzi di produzione non prodotti o non riprodotti o non ampiamente riproducibili; 'grano' e materia prima-merce 1. In questa accezione la rendita assume perciò una connotazione tecnologica dove si perde assai della distinzione tradizionale ma forse non così rilevante tra rendita e quasi-rendita, tra rendita differenziale e rendita da scarsità. Inoltre essa chiama in causa tutte le interdipendenze tra processi produttivi.

Un modello generale per le rendite, i prezzi, i salari e i profitti

Bisogna allora considerare un modello relativo alla determinazione dei prezzi e della distribuzione del reddito tra salari, profitti e rendite. Riferiamoci al più semplice dei casi possibili in cui ci sono tre processi produttivi (1) che utilizzano come mezzi di produzione merci prodotte, lavoro e 'terre' di diversa qualità e che producono 'grano' (merce 1), e un processo che produce una merce industriale (merce 2) solo con l'impiego di merci e lavoro. Sia la merce 1 che la merce 2 sono 'base' e quindi entrambe sono sia mezzi di produzione che prodotti. Dunque almeno un processo (1) deve essere in attività, perché diversamente l'economia non potrebbe funzionare. Infine il sistema economico è vitale cioè in grado di generare prodotti netti.Le equazioni (1) e (2) che seguono riguardano le relazioni tra costi, redditi (o remunerazioni) dei fattori (salari, profitti, rendite) e prezzi nella produzione delle merci 1 e 2:

I processi con terra che producono grano sono:

[a₁₁(1a)p₁ + a₂₁(1a) p₂(h)] [1+π(h)] + l₁(1a)w(h) + t₁(1a) ϱ(h) = p₁   (1a)

[a₁₁(1b)p₁ + a₂₁(1b) p₂(h)] [1+π(h)] + l₁(1b)w(h) + t₁(1b) ϱ(h) = p₁ (1b)

[a₁₁(1c)p₁ + a₂₁(1c) p₂(h)] [1+π(h)] + l₁(1c)w(h) + t₁(1c) ϱ(h) = p₁.   (1c)  

Il processo che produce la merce industriale è:

[a₁₂p₁ + a₂₂p₂(h)] [1+π(h)] + l₂w(h) = p₂(h).      (2)

Le altre relazioni del modello sono:

p1 = 1                                                                                                                (3)

Formula,                                                                                                            (4)

ϱ(1a)ϱ(1b)ϱ(1c) = 0,                                                                                         (5)

q₁(h)≤T(h)/t₁(h),        h = 1a, 1b, 1c.                                                                 (6)

I dati sono i coefficienti tecnici (di tipo 'leontieviano') di merci impiegate per unità di prodotto (a₁₁(h), a₂₁(h), a₁₂, a₂₂), di lavoro per unità di prodotto (l₁(h) e l₂) e di terra per unità di prodotto (t₁(h)). Sono date anche le entità di 'terra' T(h) di ogni qualità h=1a, 1b, 1c. La produzione della merce ottenuta dal processo h con l'uso della 'terra' di tipo h è q₁ (h), che è qui una variabile esogena e quindi non spiegata dal modello.

Le incognite sono p₁ e p₂, prezzi delle merci prodotte; w(h), il salario per unità di lavoro ('salario unitario'); π(h), il saggio di profitto; ϱ(h), la rendita per unità di terra; w è uniforme in tutti i processi e così pure π per la mobilità del lavoro e del capitale circolante.

Il significato delle equazioni è semplice: il prezzo (p) di ogni merce generata da un processo produttivo deve coprire i costi di produzione, i salari, i profitti. E, come vedremo, in taluni casi dare una rendita ai processi che usano 'terra'.

Nelle equazioni (1) compare la rendita ϱ(h) che non compare invece nella (2). Le (1) riguardano la merce 1 prodotta da un processo che usa tra i fattori anche una 'terra', scarsa e di data qualità. Per i processi (1) in attività che usano tutta la loro 'terra' si avrà una rendita positiva dovuta alla scarsità, mentre il processo meno efficiente avrà rendita zero proprio perché la 'terra' che esso utilizza non è scarsa. Tale condizione è data dalla (5) che per ora lascia impregiudicato quale sia il processo con rendita zero. I tre processi (1) dovranno essere attivati in successione, al crescere della produzione, seguendo un ordine di efficienza, non potendo ciascuno di essi produrre una quantità superiore a quella che utilizza tutta la 'terra' di una data qualità come indicato dalla (6).

L'equazione (2) riguarda l'altra merce dell'economia che non utilizza direttamente 'terra' ma ne è indirettamente condizionata utilizzando la merce 1 che è prodotta anche usando 'terra'.

Le equazioni (1) e (2) rappresentano una tecnologia multisettoriale di produzione.L'equazione (3) esprime la scelta del numerario che viene dunque identificato con la merce 1. Abbiamo dunque prezzi in termini di merce 1.

L'equazione (4) esprime la scelta esogena di una delle due variabili distributive. Si ha perciò una teoria aperta della distribuzione del reddito, per la quale la scelta della grandezza esogena tra w e π configura una valutazione economico-storico-istituzionale specifica. Assumeremo come esogeno π. Essendo stati inclusi nei coefficienti tecnici (a) i consumi di sussistenza, w sarà il salario unitario di sovrappiù per cui se w è zero il lavoro sarà pagato solo alla sussistenza storica. Nelle figure supporremo un w minimo di sussistenza pari a 1 con una semplificazione non rigorosa ma di facile intuibilità.

Risolvendo il sistema (1)-(5) si determinano i prezzi delle due merci, i saggi di rendita, il salario unitario. Ma le soluzioni non sono analiticamente semplici e si possono trovare solo facendo ricorso a sottosistemi prezzi-salario-profitto ('sottosistemi pwπ') che illustreremo qui intuitivamente (per il caso generale v. Quadrio Curzio e Pellizzari, 1996).

Rendita differenziale

Consideriamo tre casi ponendo in successione eguale a zero la rendita dei tre processi (1). Quando ϱ(1a) è zero le equazioni (1a), (2), (3), (4) (sottosistema pwπ di tipo 1a) determinano p₂(1α) e w(1α); quando ϱ(1b) è zero le equazioni (1b), (2), (3), (4) determinano p₂(1b) e w(1b); quando ϱ(1c) è zero le equazioni (1c), (2), (3), (4) determinano p₂(1c) e w(1c).

fig. 1

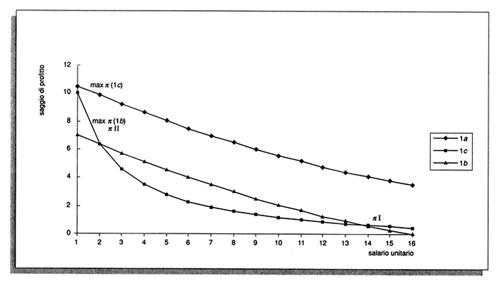
Dunque, a seconda di quale processo con terra abbia rendita zero, cambiano i prezzi e il salario. È altresì possibile individuare una relazione salarioprofitto per ogni sottosistema che evidenzia l'efficienza relativa dello stesso in quanto, a parità di π, determina il salario unitario che quel sottosistema consente di raggiungere come si vede dalla fig. 1. Ogni curva della figura è la relazione che sussiste tra salario e profitto per una tecnica (sottosistema) composta da uno dei tre processi che producono 'grano' e dal processo che produce la merce industriale. Ogni curva esprime l'efficienza, in termini di salari e profitti pagabili, di una tecnica.

E veniamo alle rendite. In base a p₂ e w, determinati in un sottosistema pwπ, le rendite si calcolano dalle equazioni (1) diverse da quella la cui rendita è zero. Abbiamo in tal modo i sei seguenti saggi di vendita:

per ϱ(1a) = 0 si calcolano ϱ(1b) e ϱ(1c);

per ϱ(1b) = 0 si calcolano ϱ(1a) e ϱ(1c);

per ϱ(1c) = 0 si calcolano ϱ(1a) e ϱ(1b).

Riferiamoci all'esempio della fig. 1 per illustrare un possibile caso.Il sottosistema di tipo 1a, e quindi il processo 1a, è più efficiente degli altri due perché a parità π ha un w sempre più alto. Se entrambi i processi 1a e 1b sono in attività e il saggio di profitto è dato, i prezzi e il salario unitario per tutto il sistema economico saranno p(1b) e w(1b), cioè in base al processo meno efficiente dei due che altrimenti non potrebbe funzionare. Così, per esempio, se π=4%, il salario unitario sarà circa pari a 6 in base al processo 1b mentre la maggiore efficienza di 1a rispetto a 1b darà luogo a una rendita per il processo 1a in proporzione alla differenza (14-6), essendo circa 14 il salario che per π=4% si avrebbe con il processo 1a se lo stesso fosse il solo attivato.In sintesi emerge così la natura della rendita. Essa nasce quando almeno due processi con 'terra' sono in attività e va a vantaggio del più efficiente di questi due processi, in quanto ha costi di produzione più bassi. La sua entità dipende dal divario di efficienza tra i due processi. Se i processi con 'terra' in attività sono tre, la rendita andrà a vantaggio dei due più efficienti.

La rendita è strutturale in quanto nasce dalla presenza di almeno due processi che utilizzano 'terra' e che producono la stessa merce, ed è differenziale in quanto dipende dalla maggior efficienza dei processi rispetto a quello che ha rendita zero. Questi aspetti strutturali prevalgono su quelli qualitativi di antica memoria, impliciti nella denominazione di rendita estensiva tipica di 'terre di diversa fertilità' attivate in successione. Ma ancora più pertinente ci appare la denominazione, già citata, di rendita tecnologica, in quanto è la scarsità di un mezzo di produzione ('terra') collegata alla natura della tecnologia multisettoriale che genera la rendita.

Ordine di efficienza

Usando antiche categorie diremmo che, quando un'economia cresce, dapprima utilizza appieno la 'terra più fertile' e poi, quando la prima è del tutto utilizzata, quelle via via meno 'fertili'. Ma quando la 'terra' è un mezzo di produzione in processi complessi come sono quelli rappresentati dalle (1) non è possibile riferirsi a un ordine di fertilità in quanto i mezzi di produzione impiegati per unità di prodotto non sono direttamente confrontabili. Se a₁₁(1a) > a₁₁(1b) e a₂₁(1a)> a₂₁(1b), l'efficienza dei processi 1a e 1b non può essere stabilita in base a confronti fisici dei mezzi di produzione ma bisogna passare ai prezzi, i quali a loro volta cambiano con la distribuzione del reddito. La misura dell'efficienza data dal 'grano per ettaro' non regge perché la produttività della terra dipende dal processo di produzione usato e il costo di produzione del grano per ettaro cambia con i prezzi, il salario e il profitto.

Ne seguono due problemi: individuare l'ordine di efficienza tra i processi 1a, 1b, 1c; stabilire come lo stesso cambia con la distribuzione del reddito, cioè di π.

Questo è ancor più vero se ci si riferisce a generici mezzi di produzione non prodotti, che non hanno una 'fertilità naturale' e la cui efficienza è inestricabile da quella del processo in cui sono inseriti. L'efficienza dei processi 1a, 1b, 1c si determina in base ai relativi sottosistemi pwπ data la variabile distributiva esogena π.

È possibile dimostrare che per ogni livello della variabile distributiva esogena π si trova l'ordine decrescente dell'altra variabile e dei prezzi come segue:

w(1a)>w(1b)>w(1c); p₂(1a)>p₂(1b)>p₂(1c).        (7)

Tale ordine è di efficienza, per cui il processo 1a è più efficiente dell'1b e questo dell'1c. Consideriamo nella fig. 1 vari casi esemplificativi con il processo 1a che è sempre il più efficiente.Se π=10,20% solo il processo 1a può essere attivato perché gli altri non sono in grado di pagare il salario minimo fissato pari a 1.

Se π=10% possono funzionare il processo 1a e 1c. Il salario sarà 1 e il processo 1a, che potrebbe pagare un salario maggiore, pari circa a 2, data l'uniformità del salario per tutta l'economia avrà invece una rendita proporzionale alla sua maggiore efficienza cioè alla differenza (2-1).

Se π=7% possono funzionare i processi 1a, 1b e 1c. Essendo l'1a e l'1c più efficienti dell'1b, a parità di salario unitario eguale a 1 essi avranno una rendita.Se 1%⟨π⟨6,10%, l'ordine di efficienza cambia e diventa 1a, 1b, 1c. Chiaro è per esempio il confronto tra il caso con π=4%, dove l'ordine di efficienza è 1a, 1b, 1c, e quello con π=8% dove l'ordine di efficienza è 1a, 1c, 1b.Dunque se cambia la distribuzione del reddito, che per noi parte dal saggio di profitto, può cambiare anche l'ordine di efficienza. Così se π cresce dal 4 all'8%, l'ordine di efficienza da 1a, 1b, 1c diventa 1a, 1c, 1b. Quest'ultimo processo addirittura non è più attivabile perché avrebbe un salario unitario inferiore al minimo ovvero risulterebbe incapace di generare un saggio di profitto così alto.

Ordine di redditività

Individuato l'ordine di efficienza, l'espansione della produzione deve avvenire seguendo lo stesso. Finché non è del tutto utilizzata una 'terra', la produzione si espande senza che cambi il numero di processi produttivi in attività. Poi ne viene introdotta un'altra e quindi aumenta il numero di processi in attività. Si passa così da un minimo di 1 processo a un massimo di 3 processi con 'terra' in attività e la tecnologia cambia dimensione.

Nell'espansione della tecnologia e delle produzioni le rendite cambiano seguendo un ordine di redditività che è la successione dimensionale delle rendite quando varia il livello di attività ma non la grandezza distributiva esogena. Sono i cambiamenti indotti nell'ordine di redditività, che può non coincidere con quello di efficienza.

Dimostriamolo supponendo che la variabile distributiva esogena π sia a un livello tale da consentire l'attivazione di tutti i processi 1a, 1b, 1c. Si può dimostrare che la rendita cresce quando calano w e p₂ e questo accade quando si introducono ulteriori 'terre' seguendo l'ordine di efficienza. Ma in tale crescita l'ordine di grandezza delle rendite, cioè l'ordine di redditività, può cambiare sia perché dipende dai coefficienti t₁(h), sia perché le variazioni di w e p₂ incidono diversamente sulle rendite.

fig. 2

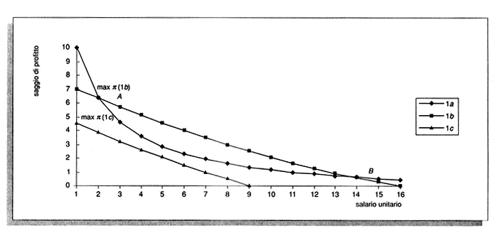
Consideriamo un caso semplificato rappresentato nella fig. 2 con il processo 1c che è sempre il meno efficiente.

Può accadere che un processo di efficienza inferiore venga ad avere una rendita maggiore di uno con efficienza superiore quando entrambi sono attivati e hanno rendita positiva.

Nella fig. 2 sono rappresentati i soliti tre processi con 'terre' (o sottosistemi pwπ) operanti. Il sottosistema meno efficiente è l'1c e quindi i processi 1a e 1b saranno perdite. È chiaro che tra le coordinate (date da π e w) dei punti A e B il processo 1b è più efficiente di 1a, ma può accadere, per opportuni valori dei coefficienti tecnici, che la rendita di 1a sia superiore a quella di 1b. In tal caso l'ordine di redditività è diverso da quello di efficienza.Oltre a questi effetti dell'espansione della produzione sulle rendite, se ne verificano altri sui salari e sui profitti (anche totali), dimostrando in tal modo la rilevanza della rendita. Si supponga, per esempio, π=7% (cioè π=max π(1b)) e che si debba espandere la produzione introducendo anche il processo 1c. Allora π deve scendere almeno fino a 4,70% (cioè a max π(1c)). In tal caso può cambiare anche l'ordine di efficienza.

Rendite in funzione del saggio di profitto

I cambiamenti nella variabile distributiva esogena π generano, in presenza di 'terre', cambiamenti nell'ordine di efficienza e di redditività, modificando la tecnologia dell'economia e i livelli di attività nonché le relazioni tra w e π. Consideriamo al proposito cinque casi stilizzati tra i molti possibili e teniamo a riferimento le figg. 1 e 2 senza analisi formalizzate.

Il primo caso (fig. 2) si ha quando sono in attività i processi 1a, 1b, 1c e il meno efficiente (1c) rimane sempre tale, pur cambiando π esogeno tra 0 e max π(1c), pari a 4,70%. La relazione tra w e π è data dalla curva 1c. Il processo 1c ha rendita zero e i processi 1a e 1b hanno rendite positive che normalmente cambieranno nelle dimensioni relative al variare di π.

Il secondo caso (fig. 1) si ha quando non cambia il processo meno efficiente in attività (sottosistema risolutivo pwπ) ma cambiano i processi con 'terra' operanti. Si considerino i processi 1b e 1c, trascurando l'1a. Nell'intervallo 10%≥π>7% opera solo il processo 1c, la cui produzione supponiamo sia sufficiente alle esigenze dell'economia. Nell'intervallo 6,10%≥π≥1% il processo 1b diventa più efficiente del processo 1c e quindi deve essere attivato. Ma se l'entità della sua 'terra' è insufficiente per soddisfare i livelli di produzione necessari all'economia, anche il processo 1c continuerà a operare. Allora il sottosistema risolutivo pwπ rimarrà quello con il processo 1c e il processo 1b avrà una rendita. In tal caso cambia la tecnologia (che passa da uno a due processi con 'terra' in attività), compare la rendita ma non cambia la relazione πw. Nell'intervallo πI>π≥0 il processo 1c diventa più efficiente del processo 1b che viene disattivato e perciò la rendita scompare. Dunque al crescere di π la rendita su 1b diventa positiva per π>πI e tale rimane fino a π=6,10% (cioè a πII) prima crescendo e poi decrescendo.

Il terzo caso (fig. 1) si ha quando, trascurando la presenza del processo 1a, operano sempre i processi 1b e 1c in quanto entrambi sono necessari data la limitatezza delle rispettive 'terre'. In tal caso la rendita sarà sempre positiva salvo che per π=πI e π=πII, ma passerà dal processo 1c al processo 1b per ritornare poi al processo 1c come risulta dalla fig. 1 per π calante da 10% a 0.

Il quarto caso (fig. 1) si ha quando il processo con 'terra' 1a è sempre attivato, mentre in alternativa operano il processo 1b o 1c per soddisfare le necessità di produzione dell'economia data la scarsità delle 'terre'. Per π che cresce da 0 a max π(1b) il processo in attività, oltre all'1a, sarà dapprima l'1c, poi l'1b, poi di nuovo l'1c. Il sottosistema risolutivo pwπ cambierà due volte e il processo 1c avrà sempre rendita.

Il quinto caso (fig. 2) si ha quando π supera un max π. In tal caso un processo deve essere disattivato e la relazione πw subisce una discontinuità. Se sono in attività tutti e tre i processi, fino a max π(1c), pari al 4,70%, i processi 1a e 1b hanno rendita. Superato max π(1c) avrà rendita solo il processo 1b; superato π(A) avrà rendita l'1a e infine, superato max π(1b), cioè il 7%, opererà solo l'1a e non ci sarà più rendita.I casi esaminati sono soltanto alcuni tra i molti possibili, ma dimostrano che i cambiamenti della variabile distributiva esogena, da noi indicata in π, a causa delle 'terre' e della rendita hanno effetti sulla tecnologia e sulla distribuzione assai più complessi di quelli dei modelli lineari di produzione-distribuzione.

Rendita intensiva

Nel caso della rendita intensiva c'è una 'terra' di qualità uniforme e di quantità data sulla quale inizialmente è utilizzato un solo processo di produzione (v. Sraffa, 1960, pp. 96 s.). Finché tale 'terra' non è scarsa non c'è rendita.

Quando, al crescere della produzione, si giunge a utilizzare tutta la 'terra' con il processo di produzione 1a, la produzione potrà ulteriormente crescere solo introducendo il processo 1b che usa la stessa 'terra' traendone una maggiore produttività in forza di un impiego di mezzi di produzione per unità di terra e di prodotto maggiore di quello di 1a.

Avendo il processo 1b un costo di produzione per unità di prodotto più alto del processo 1a, bisogna che p₁ salga fino a coprire tale costo di produzione. Ovviamente qui p₁ non è più scelto eguale a 1 e la merce 1 non è il numerario. La crescita di p₁ farà emergere una rendita da scarsità ϱ(1a) sul processo 1a che ha un costo di produzione per unità di prodotto più basso.

fig. 3

Pagando una rendita alla 'terra' usata dal processo 1a si potrebbe impedirne l'utilizzo con il processo 1b che non ha rendita. Nella fig. 3, per p₁=5 vi è una rendita per il processo 1a mentre il processo 1b non può funzionare perché il suo costo di produzione non lo consente. In tal caso però la produzione non aumenterebbe. Se la domanda continua a crescere, p₁ aumenta finché si avrà ϱ(1b) eguale a ϱ(1a) e quindi 1b potrà utilizzare una parte o tutta la 'terra' potendo pagare alla stessa una rendita così come può il processo 1a.

Continuando a crescere la domanda, cresce la quantità di 'terra' impiegata con il processo 1b in quanto la produzione del processo 1a non può più crescere. Riducendosi la 'terra' usata con 1a, T(1a), si riduce la produzione di tale processo e cresce la 'terra' usata con il processo 1b, T(1b), con un aumento di produzione. Si ha infatti: T(1a)+T(1b)=T ovvero T(1b)=T-T(1a), essendo T la quantità totale di terra disponibile.

Quando tutta la 'terra' è utilizzata dal processo 1b si disattiva il processo 1a ma non scompare la rendita, che anzi ricomincerà a crescere quando la crescita della domanda renderà necessario un ulteriore aumento di produzione con l'introduzione di un processo 1c più costoso dell'1b ma anche con una produttività della terra più alta. Vi sono fasi in cui opera un processo e fasi in cui operano due processi, e ogni volta che ne deve essere introdotto uno nuovo la rendita cresce in una misura che è tanto maggiore quanto maggiori sono i divari di costo e minori quelli di produttività dei due processi.

Le precedenti proposizioni possono essere illustrate in un caso semplificato ma chiaro (v. Montani, 1975) che noi reinterpretiamo. Supponendo di avere due sole merci, e che solo la merce 2 sia base e numerario, il sistema prezzi-distribuzione diventa:

a₂₂(1+π) + l₂w = 1,                                            (8)

a₂₁(1a)(1+π) + l₁ (1a)w + t₁(1a)ϱ(1a) = p₁   

a₂₁(1b)(1+π) + l₁ (1b)w + t₁(1b)ϱ(1b) = p₁       (9).

Per la (8), che è relativa alla merce 'industriale', si ha una relazione lineare πw per cui, dato uno dei due, si trova l'altro, mentre in base alle (9), che sono relative alla merce 'grano', si hanno due relazioni tra p₁ e ϱ date da:

ϱ(1a) = - [a₂₁(1a)(1+π) + l₁(1a)w]/ t₁(1a) + [p₁/t₁(1a)]

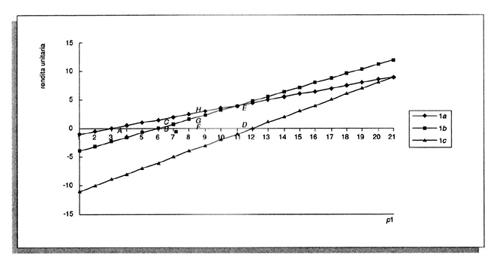
ϱ(1b) = - [a₂₁(1b)(1+π) + l₁(1b)w]/ t₁(1b) + [p₁/t₁(1b)]    (10)

i cui coefficienti sono tali da dare le relazioni (10) come rappresentate dalle rette 1a e 1b nella fig. 3, dove risulta che al crescere di p₁ crescono ϱ(1a) e ϱ(1b).Quando funziona solo il processo 1a, la rendita è zero e p₁ è OA pari a 3. Se per la crescita della domanda il prezzo sale a OB, cioè a 6, può funzionare anche il processo 1b, ma ciò non accade se il processo 1a che gode a quel prezzo di una rendita (che altri preferirebbe chiamare extraprofitto) di BC è disposto a trasferirla in tutto o in parte al proprietario della 'terra'.

Poiché per tutti i p₁ eguali o maggiori di OB e minori di OD (che è uguale a 11) il processo 1a può pagare alla 'terra' una rendita maggiore del processo 1b, esso è in grado di impedire l'uso della 'terra' al processo di 1b. Quando p₁ è diventato eguale a OD per il crescere della domanda, essendo la rendita per unità di 'terra' eguale nei due processi, entrambi possono funzionare in quanto possono egualmente pagare una rendita alla 'terra'. Al crescere della domanda si espanderà il processo 1b e si contrarrà il processo 1a senza variazione in p₁, finché sarà necessario introdurre un processo 1c secondo gli stessi criteri seguiti nel passaggio dall'1a all'1b.

Questa è la trattazione tradizionale della rendita intensiva, ma a nostro avviso si possono presentare casi più complessi, la cui soluzione dipende anche dalle entità totali dei profitti attinenti i processi 1a e 1b e quindi dalle quantità prodotte. Si consideri per esempio, tra i possibili, il seguente caso: il processo 1a, che al prezzo OB gode di una rendita pari a BC, invece di trasferirla alla 'terra' per impedire l'attivazione del processo 1b la tiene per sé. In tal modo verrà attivato anche il processo 1b che sottrarrà parte di 'terra' al processo 1a, il quale vedrà perciò ridotti i propri profitti totali ma in misura che può essere più che compensata dalla rendita e quindi tale da confermare la scelta fatta di non trasferire la stessa alla 'terra'. In tal caso la rendita intensiva sarebbe differenziale, cioè basata sulla differenza dei costi di produzione dei due processi 1a e 1b. Questa situazione potrebbe aversi fino al prezzo OD con un graduale trasferimento di rendita alla 'terra'. Così al prezzo OF andrebbe alla 'terra' una rendita di FG da parte di entrambi i processi, mentre il processo 1a terrebbe per sé una rendita di GH. Naturalmente aumentando la domanda solo il processo 1b potrà soddisfarla e quindi alla fine il processo 1a sarà disattivato.

Dunque si potrebbe dire che, sia con rendita uniforme per unità di 'terra', sia con rendita diversa, ci troviamo di fronte a una rendita strutturale intensiva perché determinata dalla scarsità di una 'terra' rispetto alla domanda e dalla differenza nei costi unitari di produzione e nelle produttività. Né è rilevante che la rendita sia pagata alla 'terra' o rimanga al processo, perché ciò che conta è la sua esistenza dovuta alla scarsità e non chi la percepisce.

Rendita tecnologica con scarsità complesse e dinamiche: ulteriori estensioni

Ai contributi di Sraffa (v., 1960) e di Quadrio Curzio (v., 1967) ne sono seguiti molti altri: quello, citato, di Montani (v., 1975) sulla rendita intensiva; quello di Abraham-Frois e Berrebi (v., 1980) sulla 'rendita differenziale esterna'; quello di Salvadori (v., 1983) sulla 'rendita singolare'; quelli di D'Agata (v., 1983 e 1984) sulla 'rendita a equilibri multipli'. Si tratta di casi assai interessanti ma analiticamente molto complessi, che non possono essere trattati qui (per una rassegna v. Kurz e Salvadori, 1995).

La precedente analisi di rendita, prezzi e distribuzione, in un contesto uniperiodale e di confronti uniperiodali, non ha considerato in modo esplicito il sistema delle quantità fisiche e la dinamica. In questa direzione sono stati elaborati modelli (v. Quadrio Curzio, 1975, 1986 e 1997; v. Quadrio Curzio e Pellizzari, 1991 e 1996) a 'tecnologie globali' (tramite coefficienti di erogazione ripartiti in una stessa tecnologia) e a 'tecnologie composte' (con tecniche lineari connesse tra loro tramite l'accumulazione dei prodotti netti che si generano nei processi entrati in stato stazionario), che ampliano e rendono probabilmente più realistico il significato della rendita tecnologica. La natura analiticamente complessa di tali estensioni rende impossibile trattarne qui e perciò ci limiteremo a orientamenti intuitivi su tre aspetti.

1. Impossibilità della crescita regolare. Con le tecnologie composte la dinamica dell'economia è a saggi variabili, diversi per le varie merci, con problemi di compatibilità strutturale tra tecniche e con possibilità di residui, cioè di prodotti netti non accumulabili. Emerge la rilevanza della 'scarsità tecnologica', che non è solo quella delle risorse scarse in natura (come la terra) ma anche quella delle tecniche che dalle stesse sono vincolate sia in scala che in struttura ma che, cambiando, possono superare le scarsità. Circa le modalità della dinamica, quella massima a saggio costante pari al saggio uniforme di prodotto netto, che è anche saggio di accumulazione, non è più possibile. Si delineano percorsi dinamici alternativi che dipendono dagli orizzonti temporali, dai residui di prodotti netti non accumulabili, dalla loro ordinabilità, dai divari dei saggi di crescita interni di ogni tecnica. Dunque viene meno quel sistema di crescita regolare e massima alla von Neumann nella quale era possibile accumulare tutto il prodotto netto ed espandere l'economia in un genere di armoniosa crescita equiproporzionale.

2. Scelta delle tecniche in relazione alla grandezza economica che si vuole massimizzare e al comportamento degli operatori. Il sistema prezzi-distribuzione e quello delle quantità fisiche diventano interconnessi causalmente, come già visto in parte, per cui le soluzioni del sistema prezzi-distribuzione influenzano quelle del sistema delle quantità fisiche che a loro volta influenzano alcune grandezze del sistema prezzi-distribuzione. Viene così meno l'indipendenza tra prezzi-distribuzione e quantità dei modelli lineari di produzione alla von Neumann e alla Leontief, che rappresentava un'altra semplificazione possibile in assenza di rendita.

Ma c'è di più in relazione al comportamento degli operatori, in quanto nella dinamica la stessa individuazione di ordini di efficienza tra tecniche con 'terra' diventa molto più articolata. Ricordiamo che l'ordine di efficienza è quello da seguire nell'attivare i processi. Ebbene, oltre a quello individuato nei precedenti capitoli sono stati individuati l'ordine dinamico-fisico, basato sui saggi uniformi di prodotto netto delle diverse tecniche e sulla compatibilità di struttura tra le stesse, e l'ordine dinamico-valori, basato sul saggio medio intertemporale di valore aggiunto al quale si deve ricorrere quando, a causa dei residui e degli orizzonti temporali diversi, è impossibile utilizzare l'ordine di efficienza dinamico-fisico.

Si è posto quindi il problema di stabilire se gli ordini di efficienza dinamici che garantiscono una crescita massima dell'economia siano compatibili con l'ordine prezzi-distribuzione che viene utilizzato dall'operatore-profitti ('imprenditore') che guida l'accumulazione e sceglie le tecnologie. La conclusione è che si può trovare un ordine di efficienza dinamico prezzi-distribuzione capace di determinare una scelta delle tecnologie da parte dell'operatore-profitti che guida il processo di accumulazione a cui corrisponde la crescita massima. Su tali basi si sono studiati gli effetti dell'accumulazione e della dinamica sulla distribuzione del reddito tra salari, profitti e rendite per quanto riguarda sia le grandezze unitarie, sia le grandezze totali, sia le quote distributive. Ne sono emerse novità che configurano diverse coincidenze o contrasti di interessi tra gli operatori che 'controllano' un fattore produttivo e che percepiscono rispettivamente salari, profitti, rendite.

3. Progresso tecnico e progresso tecnologico. Diventano una componente essenziale nello studio della rendita perché da essi dipende la scarsità e l'ordine di efficienza da seguire nella crescita. In estrema sintesi diciamo che si ha progresso tecnico quando migliora l'efficienza di una singola tecnica, si ha progresso tecnologico quando migliora l'efficienza di tutta l'economia in cui operano molte tecniche e il cui insieme dà luogo a una tecnologia. Non sempre il progresso in una tecnica si traduce nel progresso della tecnologia in quanto vi possono essere dei problemi di combinazioni di tecniche.

Le modificazioni dei prezzi e della distribuzione del reddito dovute ai diversi tipi di progresso tecnico e tecnologico individuano inoltre altre categorie di rendita tecnologica e quindi l'interesse dei diversi operatori a favore o meno dell'innovazione. Si possono così creare interessi comuni non stabili di operatori che percepiscono salari, profitti e rendite. In definitiva i problemi dell'introduzione dell'innovazione e i suoi effetti sono assai ampliati dalla presenza della rendita.

Conclusioni

Abbiamo esaminato il percorso concettuale e analitico della rendita: nata con i classici, e studiata in particolare da Ricardo, quale parte del prodotto netto che va ai proprietari terrieri per la terra ch'essi concedono in uso ai processi produttivi, la rendita si è caratterizzata principalmente per due aspetti: 1) la scarsità della terra e la sua qualità differenziata e declinante, che rallenta i processi di crescita fino a prefigurare per alcuni lo 'stato stazionario' dove la crescita cessa; 2) la natura di 'non produttori' dei percettori di rendita, che nel linguaggio comune ha configurato la categoria dei rentiers.

Per i marginalisti, essendo la terra scarsa come ogni fattore di produzione scarso, sarà remunerata in base alla sua produttività marginale; né ha rilevanza distinguere una sua specifica 'legge di formazione' rispetto ai salari e ai profitti. Per Marshall tuttavia la natura della rendita è assai più complessa, perché bisogna ben distinguere tra rendite da fattori produttivi scarsi in assoluto e quasi-rendite dovute a fattori la cui offerta può essere aumentata nel tempo.

Per i moderni studiosi della crescita e della dinamica, tra i quali i capostipiti von Neumann (v., 1937) e Harrod (v., 1948), la rendita non ha rilevanza perché non ne ha la scarsità della terra. Essi e quasi tutti i loro successori sono dei sostenitori della 'producibilità assoluta', che ha al suo opposto la 'scarsità assoluta' dei sostenitori dello stato stazionario alla Malthus.

La linea che cerca di ricomprendere l'impostazione classico-ricardiana e aspetti di quella marshalliana collocandoli in un contesto di moderne economie industrializzate e tecnologiche è quella di Sraffa (v., 1960), successivamente sviluppata da Quadrio Curzio (v. i contributi citati in bibliografia) e da altri (v. Quadrio Curzio e Pellizzari, 1996). Per questi autori, in sistemi economici circolari, cioè di produzione di merci a mezzo di merci, vi sono anche mezzi di produzione scarsi che creano la rendita. Tra questi mezzi di produzione vi sono la terra, le risorse naturali, ma anche altri mezzi di produzione che si possono assimilare alla 'terra' non per la loro natura di fattori originari ma per la scarsità, la non aumentabilità (per condizioni tecnologiche o di mercato), la necessità d'essere usati nei processi produttivi.

La teoria della rendita che abbiamo presentato si applica dunque a molti mezzi di produzione. Infatti la terra che dura (anche se deve avere una manutenzione), le miniere che si esauriscono e le macchine che incorporano un'invenzione che l'inventore non lascia diffondere, tutti percepiscono una rendita. Ma anche i mezzi di produzione prodotti e non più riprodotti e ancora in attività possono avere una rendita. E i casi si possono moltiplicare.Il progresso tecnico diventa perciò una componente fondamentale per l'entità e la durata delle rendite. Quello che riduce la necessità della terra o la rende omogeneamente più fertile riduce la rendita, così come quello che elimina il carbone a vantaggio del petrolio cancella la rendita carbonifera e crea quella petrolifera. E infine quando una 'macchina innovativa', che ha una rendita in quanto opera a fianco di altre meno efficienti, si diffonde a tutta la produzione, cessa di avere una rendita. L'ampiezza dei casi possibili ci sembra consenta di affermare che si è davvero passati dalla 'antica' rendita della terra alla 'moderna' rendita tecnologica. (V. anche Agricoltura; Distribuzione della ricchezza e del reddito; Marginalismo; Prezzi; Profitto; Risorse naturali; Salari e stipendi).

Bibliografia

Abraham-Frois, G., Berrebi, E., Rentes, rareté et surprofits, Paris 1980.

Cannan, E., A history of the theories of production and distribution in English political economy from 1776 to 1848 (1893), London 1917³ (tr. it.: Storia delle teorie della produzione e della distribuzione nell'economia politica inglese dal 1776 al 1848, Milano 1975).

D'Agata, A., The existence and unicity of cost-minimizing systems in intensive rent theory, in "Metroeconomica", 1983, XXXV, 1-2, pp. 147-158.

D'Agata, A., Molteplicità di merci agricole e rendita differenziale estensiva, in "Ricerche economiche", 1984, XXXVIII, pp. 78-94.

Fetter, F.A., Rent, in Encyclopedia of the social sciences, New York 1932, vol. XIII.

Hahn, F.H., Matthews, R.C.O., The theory of economic growth: a survey, in "Surveys of economic theory", American Economic Association-Royal Economic Society, 3 voll., London 1965, vol. II (tr. it.: Teoria dello sviluppo economico, in Il pensiero economico contemporaneo, 3 voll., Milano 1968, vol. II).

Harrod, R., An essay in dynamic theory, in "The economic journal", 1939, XLIX, pp. 14-33.

Harrod, R., Towards a dynamic economics, London-New York 1948 (tr. it.: Dinamica economica, Bologna 1990).

Hicks, J., Capital and growth, Oxford 1965 (tr. it.: Capitale e sviluppo, Milano 1971).

Kurz, D.H., Salvadori, N., Theory of production, Cambridge 1995.

Leontief, W., The structure of American economy, 1919-1929, Cambridge, Mass., 1941.

Malthus, T.R., An essay on the principle of population, as it affects the future improvement of society, London 1798 (tr. it.: Saggio sul principio di popolazione, Torino 1977).

Malthus, T.R., An enquiry into the nature and progress of rent and the principles by which it is regulated, London 1814.

Marshall, A., Principles of economics (1890), London 1920⁸ (tr. it.: Principî di economia, Torino 1972).

Meade, J., A neoclassical theory of economic growth, London 1961.

Montani, G., Scarce natural resources and income distribution, in "Metroeconomica", 1975, XXVII, pp. 68-101.

Neumann, J. von, Über ein ökonomisches Gleichungs-System und eine Verallgemeinerung der Brouwerschen Fixpunktsatzes, in Ergebnisse eines mathematische Kolloquiums, vol. VIII, Wien 1937, pp. 73-83 (tr. it.: Un modello di equilibrio economico generale, in "L'industria", 1952, n. 1, pp. 1-13).

Pasinetti, L., A mathematical formulation of the Ricardian system, in "The review of economic studies", 1960, XXVII, 2, pp. 78-98 (tr. it.: Una formulazione matematica del sistema ricardiano, in Sviluppo economico e distribuzione del reddito, Bologna 1977, pp. 9-42).

Quadrio Curzio, A., Rendita e distribuzione in un modello economico plurisettoriale, Milano 1967.

Quadrio Curzio, A., Accumulazione del capitale e rendita, Bologna 1975.

Quadrio Curzio, A., Rendita, distribuzione del reddito, ordine di efficienza e di redditività, in Contributi alla teoria della produzione congiunta (a cura di L. Pasinetti), Bologna 1977, pp. 301-327.

Quadrio Curzio, A., Technological scarcity: an essay on production and structural change, in Foundations of economics - Structure of inquiry and economic theory (a cura di M. Baranzini e R. Scazzieri), Oxford 1986, pp. 311-338.

Quadrio Curzio, A., Land rent, in The new Palgrave. A dictionary of economics (a cura di J. Eatwell, M. Milgate e P. Newman), vol. III, London-Basingstoke 1987, pp. 118-121.

Quadrio Curzio, A., Rent, distribution and economic structure: a collection of essays, Milano 1990.

Quadrio Curzio, A., Distribuzione della ricchezza e del reddito, in Enciclopedia delle scienze sociali, vol. III, Roma 1993, pp. 194-207.

Quadrio Curzio, A., Production and efficiency with global technologies, in Production and economic dynamics (a cura di M. Landesmann e R. Scazzieri), Cambridge 1997.

Quadrio Curzio, A., Pellizzari, F., Structural rigidities and dynamic choice of technologies, in "Rivista internazionale di scienze economiche e commerciali", 1991, XXXVIII, 6-7, pp. 482-517.

Quadrio Curzio, A., Pellizzari, F., Risorse, tecnologie, rendita, Bologna 1996.

Ricardo, D., Essay on the influence of a low price of the corn on the profits of stock (1815), in The works and correspondence of David Ricardo (ed. critica a cura di P. Sraffa e M. Dobb), vol. IV, Cambridge 1951.

Ricardo, D., On the principles of political economy and taxation (1817), in The works and correspondence of David Ricardo (ed. critica a cura di P. Sraffa e M. Dobb), vol. I, Cambridge 1951 (tr. it.: Principî dell'economia politica e dell'imposta, Torino 1986).

Robinson, J.V., The accumulation of capital, London 1956 (tr. it.: L'accumulazione del capitale, Milano 1961).

Salvadori, N., On a new variety of rent, in "Metroeconomica", 1983, XXXV, 1-2, pp. 73-85.

Schumpeter, J.A., History of economic analysis, 3 voll., New York 1954 (tr. it.: Storia dell'analisi economica, 3 voll., Torino 1959-1960).

Smith, A., An inquiry into the nature and causes of the wealth of nations (1776), in The Glasgow edition of the works and correspondence of Adam Smith (ed. critica a cura di R.H. Campbell, A.S. Skinner e W.B. Todd), vol. II, London 1976 (tr. it.: Indagine sulla natura e le cause della ricchezza delle nazioni, Milano 1973).

Sraffa, P., Production of commodities by means of commodities, Cambridge 1960 (tr. it.: Produzione di merci a mezzo di merci, Torino 1960).

Stigler, G.J., Production and distribution theories: the formative period, New York 1941.

Valassina, G., La teoria della rendita nella storia del pensiero economico, Milano 1976.

Wicksteed, P.H., An essay on the co-ordination of the laws of distribution, London 1894 (tr. it.: La coordinazione delle leggi della distribuzione, in La distribuzione del reddito nella teoria economica, a cura di S. Lombardini e A. Quadrio Curzio, Milano 1972, pp. 123-172).