Cerca in:
gruppo di Lie
Enciclopedia della Scienza e della Tecnica (2008)
gruppo di Lie
Luca Tomassini
Un gruppo G sul quale sia definita una struttura di varietà analitica tale che la mappa μ:(x,y)→xy−1 dal prodotto diretto G×G in G stesso sia analitica. In altre parole, [...] che lo definisce. Ogni gruppo di Lie complesso è dotato naturalmente della struttura di gruppo di Lie reale per semplice restrizione del campo complesso. Il principali esempi di gruppo di Lie sono quelli del gruppo lineare generale GL(n,ℝ) sul ...
Leggi Tutto
gruppi di Lie
Enciclopedia della Matematica (2013)
gruppi di Lie
gruppi di Lie → Lie, gruppo di. ...
Leggi Tutto
Gruppi
Enciclopedia del Novecento (1978)
Gruppi
GGeorge W. Mackey
di George W. Mackey
SOMMARIO: 1. Introduzione e storia. □ 2. Concetti fondamentali. □ 3. Anelli di endomorfismi e gruppi lineari. □ 4. La struttura dei gruppi finiti. □ 5. Gruppi [...] che soddisfi l'identità di Jacobi, L si chiama un'‛algebra di Lie' su F. L'algebra di Lie reale LG sopra definita si chiama ‛algebra di Lie del gruppo di Lie G'.
6. La struttura delle algebre di Lie e dei gruppi di Lie connessi.
Come abbiamo indicato ...
Leggi Tutto
gruppi, teoria dei
Enciclopedia della Matematica (2013)
gruppi, teoria dei
gruppi, teoria dei branca dell’algebra che si occupa dello studio dei gruppi e della loro classificazione. L’importanza del → gruppo come struttura primaria dell’algebra nello sviluppo [...] uno spazio euclideo in sé stesso. La teoria dei gruppi di Lie e quella degli omomorfismi di un gruppo in un gruppo lineare (cioè la teoria delle rappresentazioni lineari di un gruppo) diventano uno strumento indispensabile sia per il matematico sia ...
Leggi Tutto
Lie Marius Sophus
Dizionario delle Scienze Fisiche (1996)
Lie Marius Sophus
Lie 〈lìi〉 Marius Sophus [STF] (Nordfijordeid 1842 - Christiania 1899) Prof. di matematica nell'univ. di Christiania, ora Oslo (1872), di Lipsia (1886) e ancora di Christiania (1898); [...] (v. oltre). ◆ [ALG] Condizioni di L.: condizioni di integrabilità per un campo vettoriale definito su una varietà: v. gruppi di Lie: III 115 a. ◆ [ALG] Costanti di struttura di L.: v. gruppi di Lie: III 115 b. ◆ Derivata di L.: (a) [ALG] la derivata ...
Leggi Tutto
gruppi sporadici
Enciclopedia della Matematica (2013)
gruppi sporadici
gruppi sporadici locuzione, dovuta a W Burnside, con la quale si indicano complessivamente 26 gruppi finiti semplici che non rientrano nella classificazione dei gruppi finiti semplici, [...] , un gruppo finito semplice, a meno di isomorfismi, avrebbe dovuto essere di uno dei seguenti quattro tipi:
• gruppi ciclici di ordine un numero primo;
• gruppi alterni An con n ≥ 5;
• gruppi di Chevalley;
• gruppi di Lie.
Il primo gruppo che ...
Leggi Tutto
combinatòria
Enciclopedia on line
Termine con cui è anche chiamata l'algebra combinatoria, disciplina che studia, piuttosto che le strutture algebriche classiche (gruppo, anello, corpo, ecc.), le strutture algebriche di tipo più semplice, [...] metodi che risalgono a Hermann Weyl si possono anche ottenere informazioni sulle rappresentazioni dei gruppi di Lie classici.
Più interessante è la situazione per le rappresentazioni in caratteristica diversa da zero. Le rappresentazioni non sono ora ...
Leggi Tutto
CATEGORIA:
ALGEBRA
Dieudonné, Jean
Enciclopedia on line
Matematico francese (Lilla 1906 - Parigi 1992), insegnò in università francesi e di altri paesi, specialmente negli USA. Fu tra i fondatori e principali collaboratori dell'opera Éléments de mathématique [...] D. si interessò ai gruppi di trasformazioni lineari, alla teoria di Galois per gli anelli semplici e semisemplici, allo studio dei gruppi classici (lineare, simplettico, ortogonale, unitario), alla algebrizzazione dei gruppi di Lie. Tra le sue opere ...
Leggi Tutto
CATEGORIA:
BIOGRAFIE
Haar, Alfred
Enciclopedia on line
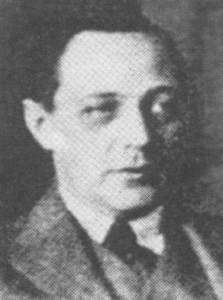Matematico ungherese (Budapest 1885 - Szeged 1933), allievo di D. Hilbert, prof. di fisica-matematica a Kolozsvár (1912) e quindi (dal 1920) di matematica a Szeged. I suoi contributi scientifici vanno [...] a J. L. von Neumann e a L. S. Pontrjagin la soluzione, per i gruppi compatti, del celebre "5º problema di Hilbert" che consisteva nel caratterizzare i gruppi di Lie mediante proprietà topologiche. Insieme con F. Riesz fondò (1922) la rivista Acta ...
Leggi Tutto
CATEGORIA:
BIOGRAFIE
trasformazione
Enciclopedia on line
trasformazione Mutamento di forma, di aspetto, di struttura.
Biologia
Trasformazione batterica
Fenomeno che si verifica spontaneamente in natura quando le cellule si trovano in uno stadio, detto competente, [...] , grazie alle proprietà a e b, appartiene sempre all’insieme.
Tra i gruppi di t. hanno particolare importanza i gruppi di Lie. Un gruppo di Lie è anzitutto un gruppo topologico (ossia uno spazio topologico S al quale è stata attribuita, con opportune ...
Leggi Tutto