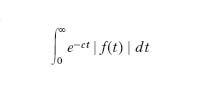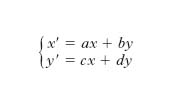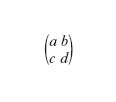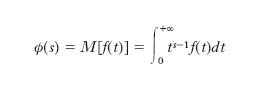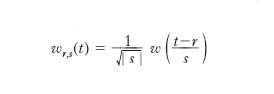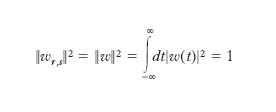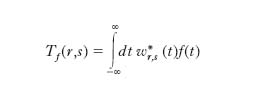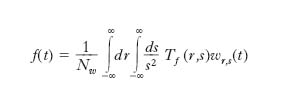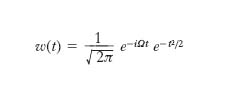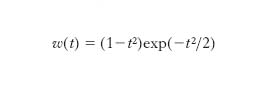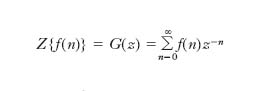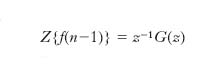trasformazione
trasformazione Mutamento di forma, di aspetto, di struttura.
Biologia
Trasformazione batterica
Fenomeno che si verifica spontaneamente in natura quando le cellule si trovano in uno stadio, detto competente, durante il quale sono attivate proteine di membrana che permettono alla cellula di incorporare DNA. Tecniche per trasformare batteri sono anche utilizzate in laboratorio per clonare i geni, cioè per introdurre, in ceppi batterici ospiti, sequenze nucleotidiche inserite in plasmidi. Poiché i plasmidi contengono per lo più geni codificanti fattori di resistenza agli antibiotici, dopo la t. è possibile selezionare i cloni delle cellule trasformate in terreni di coltura solidi contenenti antibiotici. L’elevata velocità di crescita dei batteri e la relativa semplicità con cui è possibile isolare DNA plasmidico rendono questa tecnica molto utilizzata nell’analisi di sequenze geniche e in generale nelle tecnologie di ingegneria genetica.
T. di cellule eucariotiche
Anche la t. delle cellule eucariotiche, detta transfezione, costituisce un metodo di indagine genetica di largo impiego, che permette di studiare la funzione dei geni. Le cellule usate negli esperimenti di transfezione sono per lo più cellule di mammifero in coltura (topo o uomo) e cellule di lievito opportunamente trattate (sferoplasti). I primi esperimenti di trasferimento genico sono stati realizzati mediante l’esposizione delle cellule da trattare a una soluzione di fosfato di calcio o attraverso tecniche di iniezione diretta del DNA nelle cellule mediante aghi sottilissimi. Sono stati sviluppati in seguito altri metodi, quali l’elettroporazione e l’inserimento nelle cellule di vescicole lipidiche artificiali (liposomi) o di retrovirus. Mediante l’elettroporazione le cellule sono esposte a un brevissimo impulso di corrente elettrica ad alto voltaggio che produce un’apertura dei pori dell’involucro cellulare, consentendo l’entrata del DNA estraneo. I liposomi sono utilizzati in virtù della loro composizione chimica, che consente loro di attraversare il doppio strato lipidico della membrana cellulare e riversare all’interno della cellula il DNA trasportato. I vettori virali sono invece impiegati quando è necessaria una elevata efficienza di trasferimento genico, come nel caso della terapia genica (➔ terapia).
T. neoplastica o oncogena
Conversione della cellula eucariotica, in vitro, a uno stato di crescita illimitata, simile o identico alla condizione tumorale e causato da una alterazione permanente ed ereditabile del genoma. Le cellule animali coltivate in vitro, quando sono esposte ad agenti oncogeni (alcuni virus, sostanze chimiche o radiazioni), possono subire modificazioni morfologiche e funzionali e sono chiamate cellule trasformate. Una caratteristica distintiva delle cellule trasformate è la loro somiglianza con le cellule dei tumori: sono immortali; si riproducono più velocemente delle cellule normali e danno origine a un clone, cioè a una popolazione di cellule identiche che presentano sovente forma irregolare; sopravvivono in concentrazioni molto basse di siero e possono formare colonie in terreni semisolidi; se sono coltivate su un supporto solido (superficie di una piastra o una bottiglia di coltura) non mostrano il fenomeno dell’inibizione da contatto, tipica delle cellule normali, ma continuano a crescere in strati sovrapposti. A livello della membrana si modificano sia le proteine sia i lipidi sia i carboidrati. Sulla superficie della cellula si perdono alcuni recettori e se ne formano di nuovi (per es., antigeni di trapianto tumore-specifici). Le cellule trasformate hanno inoltre funzioni cellulari alterate, quali l’aumento della glicolisi aerobia e della produzione di proteasi e la diminuzione dei livelli dell’AMP ciclico, molecola necessaria per la trasmissione di moltissimi segnali intracellulari. Tutte le cellule trasformate hanno un corredo cromosomico aneuploide e, spesso, presentano anomalie cromosomiche di struttura. I retrovirus hanno un genoma a RNA che viene trascritto a DNA e, successivamente, integrato nel genoma della cellula ospite, determinandone talvolta la t. neoplastica. Per es., la proteina trasformante del virus del sarcoma di Rous, detta P60, è stata localizzata a livello della membrana plasmatica; è una chinasi, cioè un enzima in grado di regolare l’attività di altre proteine attraverso la fosforilazione. La proteina P60 virale ha una struttura lievemente diversa da quella delle cellule normali ed è presente nelle cellule infettate in quantità 50 volte maggiore del normale. Si conoscono anche numerosi virus a DNA in grado di indurre t. cellulare, per es., il polioma, l’SV40, alcuni virus che causano tumori benigni (papillomi o polipi della pelle), alcuni adenovirus, il virus Epstein-Barr della famiglia degli herpesvirus. Studi di biologia molecolare hanno dimostrato che alcuni virus a DNA, come l’SV40 o gli adenovirus, causano la t. neoplastica perché il loro DNA si integra in prossimità di un protooncogene, alterandone la funzione. Anche le radiazioni ionizzanti e molte sostanze chimiche aromatiche, quali il benzopirene o le nitrosammine alifatiche, sono in grado di indurre t. di cellule in vitro come anche tumori in animali da laboratorio. La maggior parte di queste sostanze chimiche, per es. il benzopirene, sono precancerogene perché divengono attive solo dopo che sono state modificate chimicamente nell’organismo da parte di enzimi cellulari, detti sistemi attivanti. Per es., il sistema della monossigenasi trasforma nella cellula il benzopirene in epossidi, che causano direttamente t. neoplastica in animali da laboratorio. Per la t. in vitro è necessario che le cellule trattate possiedano il sistema attivante, oppure che vengano trattate contemporaneamente con una preparazione contenente l’enzima attivante. Lo studio delle alterazioni nelle cellule trasformate in vitro ha permesso di compiere notevoli progressi nella comprensione dei fenomeni, in gran parte simili, che si riscontrano nello sviluppo delle cellule tumorali in vivo.
Diritto
T. di società
Cambiamento del tipo di società (t. omogenea), nonché passaggio da una società di capitali ad altro tipo di ente giuridico (consorzio, società consortile, società cooperativa, comunione d’azienda, associazione non riconosciuta e fondazione), o viceversa (t. eterogenea). Risulta in ogni caso vietata la t. di una società cooperativa a mutualità prevalente in società lucrativa. La t. comporta la prosecuzione di tutti i rapporti sostanziali e processuali facenti capo alla società trasformata (principio della continuità dei rapporti giuridici). Non si ha creazione di un nuovo soggetto giuridico ma un mutamento della struttura e dell’organizzazione dello stesso ente, così che l’attività d’impresa non subisce alcuna interruzione proprio perché viene evitata la fase di liquidazione e la successiva costituzione dell’ente nella nuova forma. Le quote o le azioni vengono ripartite fra i soci proporzionalmente alla partecipazione di ciascuno e quelli fra i soci che erano illimitatamente responsabili non sono liberati dalle obbligazioni contratte anteriormente alla trasformazione. L’atto di t. deve essere redatto per atto pubblico e deve rispondere ai requisiti di forma e di contenuto previsti per l’atto costitutivo della società adottata e alle relative prescrizioni pubblicitarie. Eseguita la pubblicità nel Registro delle imprese, è esclusa la possibilità di ottenere una pronuncia di invalidità dell’atto, fermo restando il diritto dei soggetti pregiudicati di agire in responsabilità.
Le operazioni di t., fusione e scissione societaria comportano, ai fini tributari, l’applicazione di alcune disposizioni. Ai sensi dell’art. 170 del d.p.r. 917/1986 (testo unico delle imposte sui redditi, t.u.i.r.), la t. «non costituisce realizzo né distribuzione delle plusvalenze e minusvalenze dei beni, comprese quelle relative alle rimanenze e il valore di avviamento». Comportando soltanto il mutamento dello statuto societario, è considerata un’operazione non realizzativa. Essa pone, tuttavia, alcune problematiche nel momento in cui determina un cambiamento delle regole fiscali applicabili al soggetto. Esigenze di coordinamento sorgono, infatti, quando una società di persone si trasforma in una società di capitali (t. progressiva) oppure quando una società di capitali si trasforma in una società di persone (t. regressiva), atteso che la disciplina tributaria di riferimento dei due soggetti è diversa. Per soddisfare tali esigenze di coordinamento, il co. 2 dell’art. 170 t.u.i.r. prevede che, in caso di t. di società soggetta a IRES in società non soggetta a IRES, o viceversa, il reddito dell’intervallo temporale (che va dall’inizio del periodo d’imposta alla data della trasformazione) sia determinato secondo le disposizioni applicabili prima della t., in base a un apposito conto dei profitti e delle perdite. In sostanza, l’esercizio viene suddiviso in due periodi d’imposta autonomi, in relazione a ciascuno dei quali la società è tenuta a seguire la disciplina prevista. Tale coordinamento di sistemi fiscali trova completamento con i co. 3 e 4 dell’art. 170 t.u.i.r., che si occupano della sorte delle riserve costituite dalla società anteriormente al suo ingresso o alla sua uscita dalla sfera applicativa dell’IRES. L’idea di fondo è quella di assicurare alla t. la massima neutralità (continuando a garantire alle riserve il regime precedente l’operazione) e di evitare salti o duplicazioni d’imposta. La t. eterogenea è disciplinata, invece, all’art. 171 del t.u.i.r., dove si evidenzia la natura realizzativa della t. effettuata ai sensi dell’art. 2500 septies c.c. di una società soggetta a IRES in ente non commerciale. Comportando tale operazione la fuoriuscita dei beni dall’impresa, gli stessi si considerano realizzati in base al valore normale, salvo il caso in cui gli stessi confluiscano nell’azienda o nel complesso aziendale dell’ente stesso. Per quanto attiene alla fusione (➔), l’art. 172 del t.u.i.r. dispone che «non costituisce realizzo né distribuzione delle plusvalenze e minusvalenze dei beni delle società fuse o incorporate, comprese quelle relative alle rimanenze e il valore di avviamento». I maggiori valori iscritti in bilancio per effetto dell’eventuale imputazione del disavanzo derivante dall’annullamento o dal concambio di una partecipazione, con riferimento a elementi patrimoniali della società incorporata o fusa, non sono imponibili nei confronti dell’incorporante o della società risultante dalla fusione. Tuttavia i beni ricevuti sono valutati fiscalmente in base all’ultimo valore riconosciuto ai fini delle imposte sui redditi, facendo risultare da apposito prospetto di riconciliazione della dichiarazione dei redditi i dati esposti in bilancio e i valori fiscalmente riconosciuti. Il principio di fondo è quello della continuità dei valori fiscalmente riconosciuti ai beni della società estinta nella società risultante dalla fusione, al fine di evitare eventuali salti d’imposta o doppie imposizioni. Le considerazioni svolte per la fusione possono essere estese anche alla scissione (➔) societaria. Sia il principio di neutralità dell’operazione, sia quello della continuità dei valori fiscali trovano, infatti, applicazione anche per tale ultima operazione straordinaria.
Economia
Con riferimento a un sistema economico nel suo complesso, si parla di t. economica per indicare la rinuncia alla produzione di un bene per incrementare la produzione di un altro attraverso lo spostamento a questo fine delle risorse produttive rese libere. Saggio marginale di t. La quantità addizionale di un bene producibile attraverso l’impiego delle risorse liberate dalla rinuncia a produrre una unità di un altro bene.
Il settore industriale viene anche chiamato settore della t., perché trasforma materie prime in prodotti finiti.
Fisica
T. di Galileo, di Lorentz
La descrizione di un movimento facendo uso delle leggi della meccanica newtoniana presuppone di poter definire un sistema di riferimento spaziale O(xyz) e un tempo t; lo stesso fenomeno può essere descritto relativamente a un altro sistema di riferimento O′ (x′y′z′) in moto traslatorio rettilineo uniforme rispetto al precedente con velocità v; così, la posizione r′ di un punto P relativamente a O′ (x′y′z′) è descrivibile attraverso la corrispondente posizione r in O(xyz) dalla relazione r′=r+vt se per t=0 le origini O, O′ dei sistemi di riferimento coincidono. Una tale relazione, nota come t. galileiana (o di Galileo), presuppone l’esistenza di un tempo assoluto tale che, se t′ è il tempo misurato in O′ (x′y′z′), risulti t=t′. Le leggi del moto della meccanica newtoniana sono invarianti per t. di Galileo. Le equazioni di Maxwell dell’elettromagnetismo non risultano invarianti per t. di Galileo, mentre sono invarianti per t. di Lorentz (➔ Lorentz, Hendrik Antoon); ciò comporta che non esiste un tempo assoluto e pertanto lo stesso concetto di contemporaneità di due eventi deve essere completamente rivisto (➔ relatività).
T. ottica di Fourier
Tecnica ottica basata sulla proprietà per cui in particolari condizioni un sistema ottico opera su una distribuzione bidimensionale di un campo elettromagnetico una t. secondo Fourier: una tale proprietà permette di estendere ai sistemi ottici i concetti familiari della teoria delle comunicazioni elettriche, quali quelli di modulazione, filtraggio, funzione di trasferimento.
Per la t. di gauge ➔ gauge.
Linguistica
Processo per cui da una struttura profonda si genera una struttura superficiale, con operazioni di inversione, di addizione o di sostituzione ecc.: vi sono t. semplici (trasformazioni di modo, di intenzione, d’aspetto ecc.) e t. complesse (trasformazioni di descrizione, di supposizione ecc.).
Grammatica trasformazionale (o teoria trasformazionale della lingua)
Teoria e metodo (fondati dal linguista statunitense N. Chomsky) che, partendo dal presupposto che tutte le possibili realizzazioni di una qualsiasi lingua si svolgano da un ristretto numero di tipi sintagmatici fondamentali per successive t., si propongono il fine di individuare e studiare le regole alle quali queste rispondono.
Matematica
Operazione che fa corrispondere (➔ corrispondenza) a un elemento di un insieme uno o più elementi di un altro insieme, che può eventualmente anche coincidere con il primo. Il procedimento di t. trova applicazione vastissima nei campi più disparati dell’analisi, della geometria algebrica, della fisica teorica, dell’ingegneria, e pertanto il concetto di t. è suscettibile di notevoli particolarizzazioni volta per volta adatte allo studio dei vari problemi. Le principali t. sono tra spazi euclidei (come, per es., le t. di variabili), tra varietà algebriche (come le t. birazionali) o tra spazi di funzioni (come le t. di Fourier e di Laplace).
Tipologie di trasformazione
T. birazionale (o cremoniana)
T. biunivoca tra varietà algebriche nella quale i punti corrispondenti tra loro tramite la t. hanno ciascuno coordinate che sono funzioni razionali delle coordinate dell’altro. Si dice però birazionale anche una t. soltanto generalmente biunivoca, che sia cioè birazionale per tutti i punti a eccezione di alcuni, detti punti fondamentali, a ciascuno dei quali corrisponde un’intera sottovarietà, detta varietà eccezionale. T. di Fourier T. funzionale lineare che fa passare dalla funzione reale o complessa g(t) della variabile reale t, sommabile sulla retta reale, alla funzione complessa della variabile reale α definita dall’integrale
Tale integrale si dice trasformata di Fourier della g(t); di solito tale funzione non è prolungabile in una funzione olomorfa in una striscia contenente l’asse y. La t. inversa di Fourier è l’operazione mediante la quale dalla f(α) si ritorna alla g(t) che viene detta trasformata inversa (o antitrasformata) di Fourier della f(α) e che è data da:
Dalla definizione di t. e di t. inversa segue la rappresentazione di g(t) mediante l’integrale di Fourier
La t. si riduce, nel caso di funzione dispari o pari, alla sentrasformata o cosentrasformata rispettivamente. La t. di Fourier che gode di varie proprietà, per es. il teorema di convoluzione
essendo * il prodotto di convoluzione, o l’uguaglianza di Parseval, è di grandissima importanza nella matematica e nelle applicazioni.
Nelle approssimazioni numeriche la t. di Fourier si determina su un insieme finito di n punti (t. discreta di Fourier) mediante l’algoritmo della t. veloce (o rapida) di Fourier che consiste nello scomporre n nei suoi fattori, per es. n1 e n2, e calcolare n1 trasformate su n2 punti, riducendo così il numero delle operazioni (➔ DFT). T. di Hilbert T. integrali definite da:
e inversamente:
T. integrale
T. lineare tra spazi di funzioni definita mediante un integrale. Esempi importanti sono le t. di Fourier, di Laplace, di Mellin ecc. T. integrali si presentano in modo naturale quando si ha a che fare con equazioni differenziali (ordinarie o alle derivate parziali). Abbastanza tipicamente, le formule che rappresentano soluzioni di problemi iniziali o al contorno per equazioni differenziali sono, quando disponibili, trasformazioni integrali. Nell’ultimo decennio del 20° sec. l’impiego di particolari t. integrali, come le t. di Hilbert e la t. a wavelet, ha reso possibile un grande sviluppo delle tecniche di analisi, compressione e filtraggio dei segnali. Lo sviluppo degli elaboratori elettronici ha comportato inoltre un parallelo sviluppo della ricerca riguardante le t. integrali, incentrato prevalentemente sugli aspetti numerici del loro calcolo e sui problemi inerenti alla discretizzazione degli spazi di funzioni sui quali le t. agiscono.
T. di Laplace
T. funzionale lineare, introdotta da Laplace nel 1773 e anche detta t. di Laplace-Abel, che fa passare dalla funzione complessa localmente sommabile g(t) della variabile reale t, nulla per t<0, alla funzione olomorfa f(z) della variabile complessa z definita dall’integrale
e detta trasformata di Laplace della f(t). Tale integrale può essere finito o no al variare di z; l’estremo inferiore ξ delle parti reali dei numeri complessi z per cui tale integrale è finito si dice ascissa di convergenza della trasformata, e l’integrale è finito per tutti i punti del semipiano complesso la cui parte reale è maggiore di ξ. In tale semipiano f(z) risulta olomorfa. Questa t. si può estendere anche alle distribuzioni sull’asse reale, anzi sarebbe questo il suo ambito naturale; si può anche estendere alle funzioni di una variabile complessa t, integrate lungo una curva del piano complesso: in tale caso l’insieme di convergenza è una striscia parallela all’asse immaginario. L’uso della t. di Laplace è assai vasto nella matematica applicata, perché trasforma prodotti di convoluzione tra funzioni (o distribuzioni) in prodotti usuali tra funzioni olomorfe; trasforma la derivazione e l’integrazione di g rispettivamente nella moltiplicazione e divisione per z della sua trasformata; per es., trasforma un’equazione differenziale lineare a coefficienti costanti in un’equazione algebrica, detta equazione caratteristica. L’operazione e la funzione ora definite sono anche dette t. diretta e trasformata diretta di Laplace, mentre è usuale chiamare t. inversa di Laplace l’operazione mediante la quale dalla f(z) si ritorna alla g(t), che allora viene detta trasformata inversa (o antitrasformata) di Laplace della f(z), e che è data da:
i essendo l’unità immaginaria e c un numero reale tale che
non sia infinitamente grande. La relazione ora scritta è nota anche come formula di Riemann-Fourier. La t. inversa di Laplace è particolarmente importante in quanto consente di esprimere funzioni g(t) del tempo come somme di componenti sinusoidali con ampiezza variabile esponenzialmente nel tempo; come tale, è di portata più generale della t. inversa di Fourier che, infatti, si ottiene dalla [1] limitando la variabile z a valori puramente immaginari, ciò che dà luogo a componenti sinusoidali di ampiezza costante. La t. di Laplace ha grandissima importanza, oltre che nell’analisi matematica, anche in fisica matematica e in varie questioni tecniche (analisi di circuiti elettrici, propagazione di segnali elettrici, teoria dei servosistemi ecc.). T. lineare T. tra spazi vettoriali rappresentata analiticamente da equazioni lineari, cioè tale che le coordinate di un punto P′ corrispondente a P sono funzioni lineari delle coordinate di P; per es., sul piano euclideo una t. lineare è rappresentata dal sistema
e la matrice (formula)
con a, b, c, d numeri reali
si dice matrice della t. lineare. Se tale matrice è degenere, anche la t. si dice degenere. In generale, in uno spazio vettoriale S su un corpo K, con infinite dimensioni, si dice lineare una t. T che soddisfa alla proprietà: T(αx+βy)= αT(x)+βT(y), con x,y∈S; α, β∈K. Si usa anche dire che, sulla retta, l’equazione z′=(az+b)/(cz+d) esprime una t. lineare piatta; in effetti, la t. risulta lineare se si fa uso di coordinate omogenee.
T. di Mellin
T. funzionale lineare che fa passare dalla funzione complessa f(t) della variabile reale t alla funzione complessa ϕ(s) della variabile reale s così definita:
T. di Möbius
T. del piano (in particolare complesso) in sé del tipo w=(αz+β)/(γz+δ), con αδ − βγ≠0; è il tipo più generale di t. per cui a ogni valore w corrisponde un solo valore di z e viceversa. È una t. circolare. Sono t. di Möbius, per es., le traslazioni, le rotazioni, le omotetie, le inversioni; la t. di Möbius, salvo che per z=−δ/γ, è una t. conforme.
T. a wavelet
T. integrale che si è rivelata negli anni 1990 uno strumento molto utile per l’analisi dei segnali (soprattutto nel settore delle manipolazioni delle immagini e del suono elettronico) e per lo studio delle singolarità nella teoria delle equazioni differenziali non lineari, particolarmente quando i valori della funzione attorno alle singolarità sono confrontabili con i valori assunti dalla funzione nelle regioni in cui essa è regolare. La t. a wavelet è ottenuta a partire da una famiglia di funzioni wr,s(t) (dette wavelets) generate riscalando e traslando una funzione prototipo w(t)∈L2(R),
dove r,s∈R,s≠0. La funzione w(t) deve soddisfare la condizione ulteriore:
dove W(w) è la trasformata di Fourier della w(t). Viene anche imposta la normalizzazione
La t. a wavelet di una funzione f∈L2(R) è definita come:
mentre la t. inversa si ottiene da:
La wavelet prototipo può essere scelta secondo vari criteri di opportunità, per es. nel modo seguente:
dove la pulsazione Ω è spesso fissata al valore Ω=5,3 s−1, in modo che il rapporto tra il primo e il secondo massimo della parte reale della w sia pari a un fattore di circa 2. Un altro semplice esempio di wavelet è la funzione
detta anche cappello messicano (o sombrero). Trasformazione z T. integrale discreta, usata nell’ambito della scienza dei controlli per l’analisi dei sistemi discreti, che discende direttamente dalla t. di Laplace per i sistemi continui ed è definita come:
in cui f(n), con n=0, 1, 2 ecc., è la funzione campionata negli istanti t0=0, t1=T, t2=2T, t3=3T ecc., con T periodo di campionamento. Applicando la t. z all’equazione che descrive il sistema in esame, la relazione con funzione analoga a quella che, nello studio di un’equazione differenziale mediante la t. di Laplace, lega la trasformata di Laplace della derivata della funzione a quella della funzione stessa, è:
Utilizzando questa espressione è possibile calcolare la funzione di trasferimento nel sistema discreto ed effettuare le medesime verifiche di stabilità che possono essere eseguite per un sistema continuo.
Gruppo di trasformazioni
È un insieme G di t. di un insieme I in sé, il quale gode delle due proprietà: a) il prodotto di due qualsiasi t. dell’insieme G appartiene ancora a G; b) l’inversa di una qualsiasi t. di G è ancora una t. di G. Si osservi, confrontando tale definizione con quella di gruppo (➔), che si sono omesse due proprietà: quella associativa, che nel caso di un insieme di t. è sempre valida, e l’esistenza nell’insieme di un’operazione – e cioè l’identità – indifferente al prodotto, in quanto l’identità, grazie alle proprietà a e b, appartiene sempre all’insieme.
Tra i gruppi di t. hanno particolare importanza i gruppi di Lie. Un gruppo di Lie è anzitutto un gruppo topologico (ossia uno spazio topologico S al quale è stata attribuita, con opportune condizioni, una struttura di gruppo) e inoltre, in quanto gruppo di t., a ogni elemento x∈S è associata una t. di una certa varietà S′ in sé stessa. Nei casi più semplici, S′ è lo spazio euclideo En a n dimensioni. Esempi di gruppi di Lie sono i seguenti: a) il gruppo ortogonale è il gruppo delle rotazioni di En attorno a un punto assegnato, o anche è il gruppo moltiplicativo delle matrici quadrate ortogonali di ordine n; esso si indica con uno dei simboli O(n, R) oppure On(R) dove R sta a indicare che si considerano matrici a elementi reali. Lo spazio topologico S è, in questo caso, una varietà a n(n−1)/2 dimensioni subordinata allo spazio euclideo En2; in effetti, le matrici quadrate d’ordine n si rappresentano simbolicamente con i punti di En2, mentre le matrici ortogonali corrispondono a una varietà subordinata a En2 e avente dimensione n(n−1)/2. Lo spazio S′ invece è qui lo spazio lineare En; b) il gruppo ortogonale speciale è il sottogruppo di O(n, R) costituito dalle sole matrici con determinante uguale all’unità. Si indica, per es., con SO(n, R) e ha anch’esso dimensione n(n−1)/2; c) il gruppo lineare è il gruppo moltiplicativo di tutte le matrici quadrate d’ordine n a determinante diverso da zero. A seconda che si tratti di matrici con elementi reali, complessi, quaternionali, esso si differenzia in tre gruppi che si indicano con GL(n, R), GL(n, C), GL(n, H). Le rispettive dimensioni sono n2, 2n2, 4n2; d) il gruppo lineare speciale è il sottogruppo del gruppo lineare costituito dalle sole matrici con determinante uguale a 1. Si hanno perciò i gruppi GLS(n, R), GLS(n, C), GLS(n, H); e) il gruppo unitario è il gruppo moltiplicativo delle matrici unitarie (➔ matrice); esso si indica con U(n, C) o anche con U(n) ed è dimU(n)=n2; f) il gruppo unitario speciale – simbolo SU(n, C) o anche SU(n) – è il sottogruppo di U(n) costituito dalle matrici con determinante uguale a 1.
A ogni gruppo di Lie si può associare una ben determinata algebra di Lie. Si chiama con tale nome una algebra A nella quale la moltiplicazione sia anticommutativa e verifichi la cosiddetta identità di Jacobi [[α, β], γ]+[[β, γ], α]+[[ γ, α], β]=0, dove α, β, γ, sono tre elementi qualsiasi di A e le parentesi quadre indicano la moltiplicazione nell’algebra. Il più semplice esempio di algebra di Lie è costituito dagli ordinari vettori dello spazio, intendendo per moltiplicazione il prodotto vettoriale. Un importante teorema afferma che ogni algebra di Lie proviene da qualche gruppo di Lie; si comprende perciò come la classificazione delle algebre di Lie – dovuta a W. Killing, E. Cartan e altri – abbia rappresentato un passo importante verso la classificazione dei gruppi di Lie. Quest’ultimo problema è stato sostanzialmente risolto nel 1926 da O. Schreier, che è riuscito a catalogare tutti i gruppi di Lie riconducibili a una stessa algebra di Lie. Esistono inoltre particolari algebre di Lie, dette algebre di Lie graduate, in cui alcuni elementi obbediscono a regole di commutazione, come nelle usuali algebre di Lie, mentre altri elementi obbediscono a regole di anticommutazione. Precisamente, un’algebra di Lie graduata di elementi Al, Bm è definita dall’insieme delle seguenti costanti di struttura ckij, dkij, bkij: [Ai, Aj]=ckij Ak, {Bi, Bj}=dkij Ak, [Ai, Bj]=bkij Ak, dove le parentesi quadre indicano il commutatore [a, b]=ab−ba, e le parentesi graffe indicano l’anticommutatore {a, b}=ab+ba. Questo tipo di struttura è alla base delle teorie supersimmetriche in fisica teorica (➔ supersimmetria), che hanno costituito un campo di ricerca molto fecondo anche riguardo ai suoi aspetti matematici.
Operazioni sulle trasformazioni
Prodotto di t.
Siano I, I′, I″ tre insiemi, sia T una t. da I a I′ che al generico punto P fa corrispondere P′, e sia T′ una t. da I′ a I″ che al punto P′ fa corrispondere P″. Viene così a essere automaticamente definita una t. da I a I″ che a P fa corrispondere P″: tale t. si dice t. prodotto di T e T′ e si indica con T″= T′T. Per es., se I è una retta, I′ e I″ sono 2 piani, T è la t. definita da x=cost, y=sent, T′ è la t. definita da u=x+y, v=x−y, la t. prodotto T″= T′T è definita da u=cost+sent, v=cost−sent. Il prodotto tra t. non è generalmente commutativo, però è associativo, e quindi il prodotto di 3 (o più) t. si può definire così: T3T2T1=T3(T2T1)=(T3T2)T1. Potenza di una t. Se T è una t. che muta in sé un dato insieme, si dice potenza n-esima di T, e si indica con Tn, il prodotto di T per sé stessa presa n volte. Una t. tale che una sua potenza Tn sia l’identità I è detta ciclica (o periodica); si dice periodo della t. il minimo numero intero k per cui risulta Tk=I. Una t. di uno spazio S in sé tale che T2=T è detta invece idempotente; per es., la proiezione di una figura del piano su un asse coordinato. Affinché una t. sia idempotente è necessario che T, ristretta all’immagine T(S), sia l’identità.

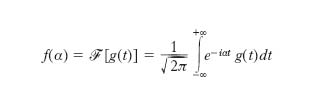
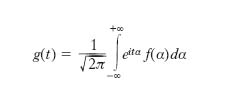
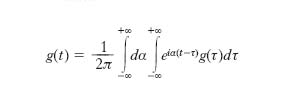
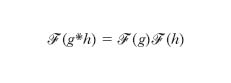
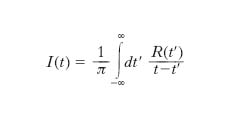
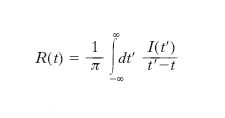
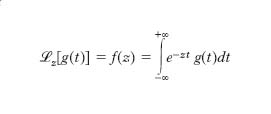
![[1] formula](https://images.treccani.it/ext-tool/intra/thumbs_medium/2/2a/FORMULE_trasformazione_08_1.jpg)