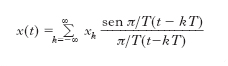campionamento
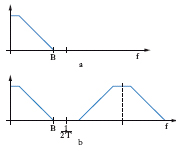
In elettronica, processo che consente di rappresentare un segnale continuo a mezzo dei valori che assume in istanti di tempo successivi. Consiste nel prelevare dal segnale a dei campioni b (fig. 1) a intervalli regolari di durata Tc ( periodo di c.), il cui inverso rappresenta la frequenza di c.; se il segnale continuo x(t) è a banda limitata B (cioè se il suo spettro di Fourier possiede ampiezza nulla per frequenze maggiori di B) e se Tc=1/2B (condizione di Nyquist), lo spettro in frequenza del segnale campionato xk=x(kT) è periodico e costituito da infinite repliche (b; fig. 2) dello spettro di x(t) (a; fig. 2). Quest’ultimo può essere quindi riottenuto dal segnale campionato per mezzo di un filtro ideale passa basso avente frequenza di taglio 1/2T. La formula per riottenere x(t) da xk è:
Se Tc non soddisfa la condizione Tc=1/2B, ma al contrario è verificata la condizione Tc>1/2B, il segnale continuo non può essere ricostruito da quello campionato, in quanto lo spettro di quest’ultimo, pur essendo sempre periodico, è pari alla sovrapposizione di bande diverse dello spettro di x(t). Questo fenomeno si manifesta con la comparsa di altre componenti (aliasing), non presenti nello spettro del segnale continuo. Se B=1/2Tc, i segnali continuo e campionato sono equivalenti, ovvero contengono la stessa informazione.
Questa trattazione teorica, detta teorema del c., costituisce la base della prima delle due operazioni fondamentali nella conversione analogico-digitale dei segnali, essendo l’altra operazione la quantizzazione.