Self-organized criticality
Self-organized criticality
Il comportamento critico autoorganizzato (self-organized criticality) si riferisce alle proprietà di una classe di sistemi, spontaneamente attratti dalla loro dinamica, a uno stato stazionario dalle proprietà critiche. Tale genere di comportamento viene tipicamente osservato in sistemi aperti con molti gradi di libertà e mantenuti in uno stato al di fuori dell'equilibrio da un processo di alimentazione-dissipazione di materia o energia. In un vasto numero di fenomeni dalcomportamento critico autoorganizzato, il processo di dissipazione si manifesta attraverso eventi di valanga che avvengono su scale temporali estremamente veloci se contrapposte alla scala temporale del processo di accumulazione di materia o energia nel sistema. Questa osservazione ha suggerito a Per Bak, Chao Tang e Kurt Wiesenfeld la formulazione, nel 1987, del primo modello per il comportamento critico autoorganizzato che esemplifica i meccanismi dinamici generanti l'evoluzione spontanea verso il punto critico. Questo modello ha dato vita a un ampio dibattito sui sistemi autocritici, come talvolta essi vengono definiti, ed è stato adottato come sistema prototipo per la discussione sul comportamento critico autoorganizzato, sia nell'ambito specialistico della fisica statistica, sia in un vasto numero di discipline come la geofisica, la cosmologia, la biologia, l'ecologia, l'economia, le neuroscienze e la sociologia.
Lo studio delle transizioni di fase nella materia ha avuto il suo culmine con la comprensione dei fenomeni critici e delle loro caratteristiche: divergenza della lunghezza di correlazione, invarianza di scala e funzione di risposta anomala ‒ estesa a tutte le scale, sia spaziali sia temporali ‒ anche nel caso di una perturbazione infinitesima. Tipicamente però, i fenomeni critici vengono osservati solo a un valore particolare di un parametro di controllo esterno. Esempi classici sono il valore critico della temperatura delle transizioni di fase del secondo ordine, della soglia di percolazione o il valore di biforcazione dei sistemi dinamici.
Leggi di invarianza di scala e funzioni di risposta anomala emergono però in molti fenomeni naturali che non sono riconducibili a specifiche transizioni di fase o al valore particolare di uno specifico parametro di controllo. Si parla in questi casi di invarianza di scala generica, sollevando tuttavia la questione della ricerca dei meccanismi in grado di generare tali fenomeni senza bisogno di alcuna transizione di fase. Un esempio classico, e allo stesso tempo di enorme rilevanza scientifica, di invarianza di scala generica si riscontra nello studio dei terremoti. Nel caso dei terremoti, l'energia accumulata tramite il lento movimento delle placche tettoniche viene rilasciata in modo improvviso, sotto forma di onde sismiche, quando la deformazione della crosta terrestre oltrepassa una determinata soglia. È evidente tuttavia che nei terremoti non è possibile identificare un parametro critico, modificabile dall'esterno, che determini la presenza di proprietà critiche. Il comportamento tipico dei fenomeni critici viene osservato in un vasto numero di fenomeni in cui la dinamica procede in forma di valanghe attraverso una dinamica in cui, a una lenta accumulazione di materia o energia nel sistema, segue un rilascio improvviso ed estremamente veloce di ampiezza non predicibile.
Il modello BTW
Partendo dalla constatazione che la dinamica a valanghe sembra essere alla base di un vasto numero di fenomeni dal comportamento critico autoorganizzato, Bak, Tang e Wiesenfeld hanno proposto, nel 1987, un semplice modello in forma di automa cellulare che può essere considerato la pietra miliare dei cosiddetti modelli di autoorganizzazione critica, o modelli SOC (Self-organized criticality). Il modello BTW, dal nome degli autori, è un semplice automa cellulare discreto, definito su un reticolo D-dimensionale in cui a ogni cella i del reticolo viene associata una variabile zi che possiamo identificare con la materia o l'energia accumulata sulla cella medesima. A ogni istante di tempo t, misurato in intervalli discreti, un'unità di materia o energia viene aggiunta nel sistema su una cella i scelta a caso, cosicchè zi→zi+1. A ogni cella viene però associata una soglia critica locale zc tale che, quando zi≥zc, la cella rilascia l'energia accumulata distribuendola ai suoi vicini in accordo con le seguenti regole:
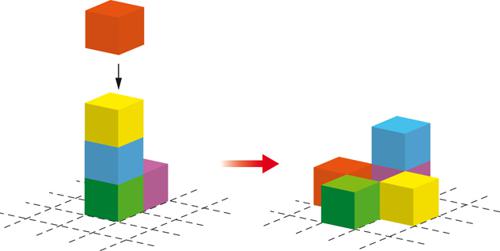
[1] zi → zi − zc
[2] zj → zj + yj
dove con j identifichiamo tutte le celle in contatto con la cella i e ∑jyj=zc. Per esemplificare tale procedura, possiamo pensare a un reticolo bidimensionale, come una classica scacchiera, dove ogni casella è capace di accumulare fino a quattro unità di massa o energia. A questo punto, le quattro unità vengono rilasciate e ripartite nelle quattro caselle vicine in modo omogeneo, come illustrato in fig. 2. Il rilascio di materia o energia dalla cella i può essere però determinante per far raggiungere la soglia critica zc a una o più celle vicine, che possono avere già immagazzinato altre unità di energia, e avviare quindi altrettanti eventi di rilascio che a loro volta possono generare una reazione a catena, dando vita a una valanga di materia o energia attraverso il sistema. Il modello originale considera che l'energia venga infine dissipata lasciando i bordi del sistema aperto, ovvero le unità di energia che escono dal reticolo vengono considerate definitivamente perse. Di conseguenza ogni valanga, qualunque sia il numero di celle o unità di energia coinvolte, viene alla fine dissipata e il sistema torna a uno stato in cui tutti i siti si trovano al di sotto della soglia critica locale zc. Soltanto quando il sistema è di nuovo in uno stato di riposo, l'energia viene aggiunta un'altra volta al sistema in maniera casuale come descritto precedentemente. Questo fa sì che la valanga dei processi di rilascio possa essere considerata istantanea rispetto alla scala temporale di aggiunta di materia o energia.
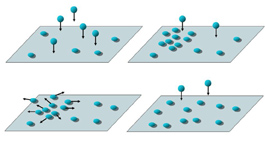
Un modello SOC è dunque necessariamente un sistema dissipativo, che, come nel caso dei terremoti, accumula stress o energia in maniera molto lenta. La soglia locale crea dei processi di rilascio che ridistribuiscono l'energia localmente, ma, quando l'energia totale presente nel sistema è sufficientemente elevata, si possono generare delle valanghe di eventi di rilascio che alla fine dissipano l'energia al di fuori del sistema, come illustrato in fig. 3. Il modello può essere facilmente simulato con l'ausilio del calcolatore e si può mostrare che la dinamica raggiunge uno stato stazionario in cui l'energia totale del sistema è pressoché costante, mentre l'attività di rilascio avviene attraverso valanghe che coinvolgono un numero di celle s con una probabilità P(s) secondo la legge di potenza
[3] P(s) ∼ s−τ
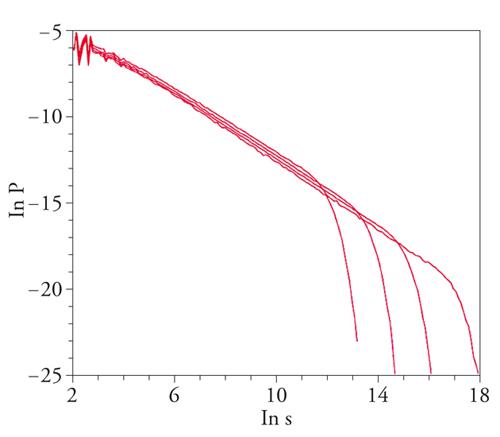
dove τ è un esponente che dipende dalla dimensione euclidea del reticolo. Simili leggi di potenza vengono osservate anche per le probabilità P(l) e P(t) che una valanga si estenda per una lunghezza caratteristica l e abbia una durata temporale t. Analogamente a quanto avviene nei fenomeni critici, gli esponenti critici di tali distribuzioni sono legati da opportune relazioni, dette relazioni di scala. È anche importante notare che nelle simulazioni numeriche le leggi di potenza sono limitate dalla taglia finita del reticolo (fig. 4). Usando reticoli di taglia sempre più grande è possibile però osservare che la legge di potenza diviene sempre più estesa e le distribuzioni ottenute per diverse taglie del sistema possono essere usate ‒ tecnica del collasso dei dati di taglia finita ‒ per ottenere il valore preciso degli esponenti critici.
Il modello BTW ritrova dunque, attraverso un meccanismo estremamente semplice, la presenza di comportamento critico e di invarianza di scala, proprio come osservato nei processi di valanga. Inoltre, il comportamento critico viene raggiunto dal sistema in modo spontaneo, senza l'apparente bisogno di regolare i parametri del sistema a un valore specifico. Il comportamento critico del modello appare infatti essere indipendente dai valori scelti di zc, e dal meccanismo di redistribuzione yi. Il modello risulta inoltre stabile rispetto ad altre interessanti variazioni, come l'introduzione di un processo di rilascio stocastico in cui le unità di energia vengono ripartite nei siti vicini in maniera casuale, o la presenza di meccanismi di dissipazione locale che provocano l'uscita di energia dal sistema durante il processo di rilascio stesso. Tali proprietà di stabilità rispetto alle variazioni della dinamica macroscopica sono state una delle ragioni più importanti per cui i modelli SOC sono stati accolti come una spiegazione plausibile per l'ubiqua presenza di invarianza di scala e di comportamento critico nei fenomeni naturali.
Il modello BTW e le sue variazioni vengono anche definiti come i modelli del mucchio di sabbia. Se infatti prendiamo un mucchio di sabbia e vi aggiungiamo lentamente degli altri granelli di sabbia, il mucchio diventa più alto e ripido fino al raggiungimento di una certa altezza oltre la quale la sua ripidezza non può più aumentare. L'aggiunta, a questo punto, di nuovi granelli di sabbia provoca delle frane, degli scivolamenti di valanghe di una certa quantità di sabbia lungo le pareti. Le frane ovviamente sono di magnitudine variabile, coinvolgendo alcune volte solo pochi granelli di sabbia, altre volte larghe parti delle pareti del mucchio di sabbia. Non è quindi difficile vedere un'analogia con il processo descritto dal modello BTW, di frequente esemplificato attraverso l'esempio dei mucchi di sabbia. Il modello BTW può anche essere opportunamente modificato creando delle soglie di stabilità locali, dette laplaciane, dove la stabilità non è data da un numero assoluto, ma dalla differenza di unità di materia o energia tra siti adiacenti. In questo caso, il modello crea realmente una struttura della variabile zi che definisce una forma simile a un mucchio di sabbia, rendendo l'analogia ancora più realistica. Essa è stata pure estesa ai mezzi granulari in maniera più generale, e diversi esperimenti sono stati eseguiti al fine di ottenere il comportamento critico autoorganizzato in sistemi granulari (dalla sabbia fino al riso alimentare), sottoposti alla stessa dinamica definita nel modello BTW. Mentre il calcolatore viene di norma utilizzato per simulare fenomeni reali, nel caso del modello BTW si è cercato invece di ottenere una realizzazione sperimentale dell'automa definito al calcolatore.
Il modello BTW è stato spesso discusso in letteratura come il tipico esempio di sistema con comportamento critico nel quale nessun parametro critico deve essere fissato a un valore opportuno. Questa asserzione è tuttavia inesatta, in quanto nella definizione dell'automa cellulare è implicitamente presente una condizione determinante per la presenza dell'invarianza di scala. Nella definizione dell'automa cellulare, appena una cella inizia un processo di rilascio di energia, l'aggiunta di energia viene arrestata fino a che il sistema non raggiunge nuovamente uno stato stabile in cui tutte le celle si trovano al di sotto della soglia critica locale. Tale condizione rappresenta la completa separazione di scala temporale tra l'aggiunta di materia o energia e l'evoluzione della valanga. In altre parole, il modello fissa implicitamente a zero il rapporto tra le due scale temporali tε e th che caratterizzano rispettivamente la dissipazione e l'aggiunta di energia o di materia. Si è dimostrato che una simile condizione, apparentemente innocua, è invece necessaria per ottenere la completa invarianza di scala del sistema: appena il rapporto tra le scale temporali è diverso da zero, l'invarianza di scala viene verificata solo fino a una certa scala caratteristica sc per la taglia delle valanghe, che diventa infinita soltanto nel limite tε/th→0. Denominata tecnicamente separazione infinita di scale temporali, questa condizione è facilmente definita nelle regole dell'automa cellulare, e implementata nell'algoritmo utilizzato per le simulazioni al calcolatore. Tuttavia, nei fenomeni naturali è impensabile avere un'infinita separazione di scale temporali, ed è quindi plausibile pensare che esista sempre, in generale, una lunghezza caratteristica oltre la quale l'invarianza di scala e la fenomenologia critica vengano meno. Quanto detto viene infatti osservato in molti sistemi naturali menzionati precedentemente. La presenza di un parametro critico implicito nel modello non deve però essere confusa con l'equivalenza rispetto ai fenomeni critici usuali. Mentre il fissare un parametro di controllo a un valore critico preciso è un esercizio estremente difficile, e quindi improbabile come spiegazione generale della presenza di fenomeni critici autoorganizzati, l'esistenza di fenomeni determinati da dinamiche con scale temporali estremamente diverse è un evento molto comune, come abbiamo visto nel caso dei terremoti, che si candida a meccanismo generale per l'ubiquità dell'invarianza di scala in natura.
Nonostante la semplicità delle regole del modello BTW, una soluzione analitica rigorosa e generale non è ancora disponibile. Alcuni casi particolari, come i cosiddetti modelli diretti in cui il rilascio di energia è vincolato ad avvenire in una determinata direzione, sono stati risolti con sofisticate tecniche matematiche e di teoria dei campi. Una comprensione di base, anche se approssimata, dei modelli SOC si può raggiungere grazie all'uso di teorie di campo medio, che hanno infatti messo in luce il ruolo delle scale temporali del meccanismo di aggiunta-dissipazione di energia. Teorie di rinormalizzazione in spazio reale sono capaci di calcolare in maniera approssimata gli esponenti critici. Una teoria di campo che traccia delle analogie tra le transizioni di fase assorbenti nei processi di contatto e i modelli tipo BTW lascia intravedere la possibilità di calcoli perturbativi di teoria dei campi anche nel caso generale. Tuttavia, una teoria rigorosa e generale dei modelli tipo BTW non è ancora disponibile. Il semplice automa, così facilmente definibile attraverso poche righe di un programma di computer, si è rivelato una formidabile sfida teorica per un grande numero di fisici statistici.
Altri modelli
Il modello BTW ha spinto la comunità scientifica a definire una vasta gamma di modelli che, seguendo regole dinamiche analoghe, ritrovano la presenza di comportamento critico autoorganizzato. In alcuni casi questi modelli sono stati ispirati a un maggiore realismo e alle simulazioni di alcuni sistemi specifici. In altri casi, la formulazione del modello è stata dettata dalla ricerca di un'ulteriore semplificazione della dinamica che rendesse possibile una soluzione analitica rigorosa pur preservando il comportamento critico autoorganizzato.
Un tipico esempio della tendenza a un maggiore realismo è rappresentata dal modello d'incendio delle foreste introdotto da Barbara Drossel e Franz Schwabl, dove a ogni sito del reticolo è associata la presenza omeno di un albero. Nei siti vuoti un albero cresce con probabilità p, mentre con probabilità f la caduta di un fulmine genera l'incendio di un albero esistente. Esso trasmette a sua volta l'incendio agli alberi adiacenti, generando degli incendi la cui portata varia in maniera probabilistica. Tale modello genera comportamento autocritico, anche in questo caso nel limite di infinita separazione delle scale temporali della crescita degli alberi (molto lenta) e della trasmissione del fuoco ad alberi adiacenti (estremamente veloce). Compare tuttavia una terza scala temporale, determinata dalla probabilità f che un albero prenda fuoco. Questo parametro aggiunge dunque una seconda condizione di separazione delle scale temporali, in quanto la caduta di fulmini deve essere molto più rara, lenta quindi, se vogliamo che la foresta possa crescere e dar vita a incendi di grandezza macroscopica. È un modello molto interessante, in quanto la doppia separazione di scale temporali è facilmente riconducibile a condizioni reali: gli incendi si trasmettono infatti molto più velocemente di quanto non crescano gli alberi che, a loro volta, vengono colpiti da un fulmine solo molto raramente, aspettando quindi in media un tempo lunghissimo prima che si possa generare un incendio. In un simile regime, però, il modello genera incendi le cui proporzioni hanno una probabilità che segue una legge di potenza e quindi comportamento autocritico. È interessante osservare come la legge di probabilità delle dimensioni di incendi casuali abbia, in alcuni esperimenti, proprietà simili a quelle osservate nel modello.
Vogliamo infine riportare la definizione di un modello estrememente semplificato e che ha dato vita alla classe dei modelli estremali con comportamento critico autoorganizzato. Il modello introdotto agli inizi degli anni Novanta del XX sec. da Bak e Kim Sneppen, rappresenta una distillazione concettuale del modello BTW. Il modello viene originariamente definito in un reticolo unidimensionale ‒ una catena lineare con N celle ‒ in cui a ogni cella i viene associata una variabile ri scelta a caso tra i numeri reali dell'intervallo [0,1]. A questo punto la dinamica procede attraverso i seguenti semplici passi: (a) la cella con il numero più basso viene aggiornata con un nuovo valore ri scelto a caso nell'intervallo [0,1] e lo stesso avviene per le due celle adiacenti ri+1 e ri−1; (b) se una delle due celle adiacenti contiene il numero più basso tra tutte le celle N, il processo continua; nel caso contrario, si trova nel sistema quale altra cella abbia il valore minimo e si inizia nuovamente il processo di aggiornamento dei numeri.
Tale dinamica, detta di tipo estremale dato che viene sempre aggiornata solo la cella con il valore ri più basso, anche se di una semplicità estrema produce tutte le proprietà tipiche dei sistemi con comportamento critico autoorganizzato. Dopo un numero estremamente ampio di iterazioni, il sistema converge in uno stato stazionario in cui è impossibile trovare valori di ri minori di una certa soglia rc=2/3. In questo stato stazionario è anche possibile definire una valanga come la serie n di celle contigue che vengono aggiornate. La probabilità P(n) che la valanga coinvolga n celle è anche in questo caso in forma di legge di potenza P(n)∼n−θ, dove θ è l'esponente critico. La semplicità di questo modello, che ha reso possibile lo sviluppo di tecniche analitiche per la sua soluzione, non deve però far pensare a una completa astrazione dalla realtà. Motivazioni del modello si ritrovano infatti in campi piuttosto lontani dalla fisica statistica, come l'ecologia e la paleontologia.
In questo ultimo caso le celle sono una rappresentazione astratta di altrettante specie animali. Il numero associato a ogni specie quantifica la sua adattabilità, che in qualche modo ne rappresenta la capacità di sopravvivenza e, quindi, di non estinzione. Ovviamente, riassumere un concetto così complicato in un solo numero deve essere considerato come un'approssimazione estrema, finalizzata alla semplificazione del modello. La dinamica del modello, dunque, non fa altro che determinare l'estinzione della specie con l'adattabilità più piccola e la sua sostituzione con una nuova specie con una nuova adattabilità. È evidente che la scomparsa di una specie influisce su un certo numero di altre specie (per es., i suoi predati o predatori), che consideriamo essere rappresentate dallecelle adiacenti, cambiandone l'adattabilità. Se le specie collegate subiscono cambi di adattabilità sfavorevoli si estingueranno a loro volta, facendo sì che ogni valanga di n celle corrisponda all'estinzione di n specie connesse. Naturalmente, questo modello è una semplificazione estrema del processo ed è indubbio che debba essere considerato come un modello giocattolo della dinamica delle estinzioni. Tuttavia, gli studi paleontologici hanno trovato che la probabilità di estinzioni di massa che coinvolgono un numero di specie n segue proprio una legge di potenza, rendendo non del tutto inaccettabile che un modello di tale semplicità possa rappresentare la dinamica di un processo così complesso come l'estinzione di una specie.
L'esempio del modello di Bak e Sneppen dimostra come la modellizzazione dei fenomeni con comportamento critico autoorganizzato abbia condotto la fisica statistica al di fuori dei suoi usuali confini di interesse. La diversità dei campi scientifici in cui il comportamento critico autoorganizzato è rilevante ha introdotto l'applicazione di metodologie e tecniche della fisica statistica e dei sistemi complessi in discipline molto lontane da essa, contribuendo notevolmente alla definizione della fisica interdisciplinare che negli anni Novanta del XX sec. ha trovato una sua identità precisa, ora riconosciuta dalle maggiori società mondiali di fisica.
Bibliografia
Bak 1988: Bak, Per - Tang, Chao - Wiesenfeld, Kurt, Self-organized criticality, "Physical Review A", 38, 1988, pp. 364-374.
Bak 1996: Bak, Per, How nature works: the science of self-organized criticality, New York, Copernicus, 1996.
Bak, Sneppen 1993: Bak, Per - Sneppen, Kim, Punctuated equilibrium and criticality in a simple model of evolution, "Physical review letters", 71, 1993, pp. 4083-4086.
Buchanan 2003: Buchanan, Mark, Ubiquità: dai terremoti al crollo dei mercati, Milano, Mondadori, 2003.
Drossel, Schwabl 1992: Drossel, Barbara - Schwabl, Franz, Self-organized critical forest-fire model, "Physical review letters", 69, 1992, pp. 1629-1632.
Vespignani, Zapperi 1998: Vespignani, Alessandro - Zapperi, Stefano, How self-organized criticality works: a unified meanfield picture, "Physical review E", 57, 1998, pp. 6345-6362.